फलन y=f(x) का आरेख संगलन चित्र में दर्शाया गया है। चार सीमाएं निम्नानुसार है
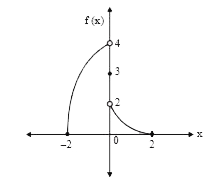
तब का मान है [f Vii : kh : [k], k] से छोटे या बराबर महत्तम पूर्णांक को निरूपित करता है
The correct Answer is:
Topper's Solved these Questions
- फलन की सीमा सत्त्यता तथा अवकलनीयता BOOK - BANSAL HINDICHAPTER - फलन की सीमा सत्त्यता तथा अवकलनीयता EXERCISE - Exercise -1 Special DPP-3 [LIMIT]
14 Videos
- फलन की सीमा सत्त्यता तथा अवकलनीयता BOOK - BANSAL HINDICHAPTER - फलन की सीमा सत्त्यता तथा अवकलनीयता EXERCISE - Exercise -1 Special DPP-4 [LIMIT]
14 Videos
- फलन की सीमा सत्त्यता तथा अवकलनीयता BOOK - BANSAL HINDICHAPTER - फलन की सीमा सत्त्यता तथा अवकलनीयता EXERCISE - Exercise -1 सत्य एव असत्य
15 Videos
- क्रमचय एवं संचय BOOK - BANSAL HINDICHAPTER - क्रमचय एवं संचय EXERCISE - EXERCISE-5 (RANK BOOSTER )
12 Videos
- वृतBOOK - BANSAL HINDICHAPTER - वृतEXERCISE - EXERCISE - 5
10 Videos
Similar Questions
limx→∞cos(x2)cos(x4)cos(x8)..cos(x2n)का मान है
View SolutionLimx→∞(x2−2x+1x2−4x+2)x=
View Solution(a) Limx→4(2xx−4−8x−4)=Limx→42xx−4−Limx→48x−4
(b) Limx→1x2+6x−7x2+5x−6=Limx→1(x2+6x−7)x2+5x−6x→1
(c) Limx→1x−3x2+2x−4=Limx→1(x−3)Limx→1(x2+2x−4)
(d) यदि Limx→5f(x)=2 और =x→50 हो तो, Limx→5f(x)g(x) विध्यमान नहीं है
यदि f(x)x→5=0 और Limx−5g(x)=2 हो तो, Limx→5f(x)g(x) विध्यमान नहीं है
View Solution8 चप्पु वाले नाव के सदस्यो को 11 पुरुषों में से चयनित करना है। जिसमें से 5 केवल स्ट्रोक साइड, 4 केवल बो साइड और बाकि दो किसी भी तरफ लिये जा सकते है। कुल कितने चयन संभव है?
View Solutionएक बिन्दु एक ऐसे वृत्त (x+4)2+(y+2)2=25 के अनुदिश गतिमान है जिसका केन्द्र C है। वह वृत्त से बिन्दु A या बिन्दु B पर अलग हो जाता है तथा स्पर्श रेखा के अनुदिश गति करता हुआ बिन्दु D (3.-3) से गुजरता है। निम्न को ज्ञात कीजिये।
(i) A व B पर स्पर्श रेखाओं के समीकरण
(ii) A व B के निर्देशांक
(iii) कोण ADBC व् D की वृत्त से अधिकतम व न्यूनतम दूरी
(iv) चतुर्भुज ADBC व त्रिभुज DAB का क्षेत्रफल
(v) त्रिभुज DAB के परिवृत्त का समीकरण तथा इस वृत्त के द्वारा निर्देशी अक्षों पर काटे गये अन्तः खण्ड
View SolutionL_(1)=x+3y-5=0,L_(2)=3x-ky-1=0,L_(3)=5x+2y-12=0 are concurrent if k=
View SolutionGraph of a function y=f(x) is shown in the adjacent figure.Four limits l_(1),l_(2),l_(3) and I_(4), are given as:
View SolutionLet limx→0sin2Xtan(x2)=L, and limx→0e2x−1x=L2 then the value of L1L2 is
View SolutionIf l1=∫nπ0f(|cosx|)dx and l2=∫5π0f(|cosx|)dx, then
View Solutionमाना कि f:(0,∞)→R एक अवकलनीय फलन इस प्रकार है कि f'(x)=2−f(x)x सभी x∈(0,∞) तथा f(1)≠1 के लिए । तो :
(a) fx→0+'(1x)=1
(b) limx→0+xf(12)=2
(c) limx→0+x2f'(x)=0
(d) |f(x)|≤2 सभी x∈(0,2) के लिए
View SolutionLet f(x)=Limn→∞2x2nsin1x+x1+x2n then find
Limx→0f(x)
View SolutionIf f(x)={2x+3x≤03(x+1)x>0 then the value of limx→0f(x) is
View SolutionConsider the lines
L1:x+y=10, L2:x+y=60
L3:x=40, L4:y=40.
L1 meets x - axis and y - axis at A and B respectively.
L4 meets y - axis at C and L2 at D
L3 meets L2 at E and x-axis at F.
Perimeter of the hexagon ABCDEF is
View Solutionमाना f(0)= 0 तथा f'(0)= 1 है। धनात्मक पूर्णांक k के लिए प्रदर्शित कीजिये की
Limx→01x(f(x)+f(x2)+……f(xk))=1+12+13+…..+1k
View Solution(a) यदि Limx→−2f(x)x2=1 हो तो ज्ञात कीजिए (i) Limx→−2f(x),(ii)Limx→−2f(x)x
View Solution
