A block of 200 g mass moves with a uniform speed in a horizontal circular groove, with vertical side walls of radius 20 cm. If the block takes 40 s to complete one round, the normal force by the side walls of the groove is :
To solve the problem, we need to find the normal force exerted by the side walls of a horizontal circular groove on a block moving in it. Here’s a step-by-step breakdown of the solution:
Step 1: Convert the mass and radius to standard units
- The mass of the block is given as 200 g. We need to convert this to kilograms:
m=200g=200×10−3kg=0.2kg
- The radius of the groove is given as 20 cm. We need to convert this to meters:
R=20cm=20×10−2m=0.2m
Step 2: Determine the time period
- The block takes 40 seconds to complete one round. Thus, the time period T is:
T=40s
Step 3: Calculate the angular velocity
- The angular velocity ω can be calculated using the formula:
ω=2πT
- Substituting the value of T:
ω=2π40=π20rad/s
Step 4: Calculate the linear velocity
- The linear velocity V can be calculated using the relationship between linear and angular velocity:
V=R⋅ω
- Substituting the values of R and ω:
V=0.2⋅π20=0.2π20=π100m/s
Step 5: Calculate the centripetal force
- The normal force N provides the necessary centripetal force for circular motion. The formula for centripetal force is:
N=mV2R
- First, calculate V2:
V2=(π100)2=π210000
- Now substituting m, V2, and R into the equation for N:
N=0.2⋅π2100000.2=π210000
Step 6: Calculate the numerical value of the normal force
- Using π≈3.14:
N=(3.14)210000=9.859610000=0.00098596N≈9.86×10−4N
Final Answer
The normal force exerted by the side walls of the groove is approximately:
N≈9.8×10−4N
---
- The mass of the block is given as 200 g. We need to convert this to kilograms:
m=200g=200×10−3kg=0.2kg
- The radius of the groove is given as 20 cm. We need to convert this to meters:
R=20cm=20×10−2m=0.2m
- The block takes 40 seconds to complete one round. Thus, the time period T is:
T=40s
- The angular velocity ω can be calculated using the formula:
ω=2πT
- Substituting the value of T:
ω=2π40=π20rad/s
- The linear velocity V can be calculated using the relationship between linear and angular velocity:
V=R⋅ω
- Substituting the values of R and ω:
V=0.2⋅π20=0.2π20=π100m/s
- The normal force N provides the necessary centripetal force for circular motion. The formula for centripetal force is:
N=mV2R
- First, calculate V2:
V2=(π100)2=π210000
- Now substituting m, V2, and R into the equation for N:
N=0.2⋅π2100000.2=π210000
- Using π≈3.14:
N=(3.14)210000=9.859610000=0.00098596N≈9.86×10−4N
The normal force exerted by the side walls of the groove is approximately:
N≈9.8×10−4N
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS (SECTION B)
30 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS SECTION A
60 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - (SECTION - B)
10 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
A small block of mass 100g moves with uniform speed in a horizontal circular groove, with vertical side walls of radius 25cm. If the block takes 2.0s to complete one round, find the constant force by the side wall of the groove.
View SolutionA small block of mass 100 g moves wth uniform speed n a horizontal circular groove, with vertical side walls, of radisu 25 cm.If the block takes 2.0 s to complete ne round, find the normal contact force by tehside wall of the groove.
View Solution
Knowledge Check
An insect trapped in circular groove of radius 12 cm moves along the groove steadily and completes 7 revolutions in 100s. The linear speed of the insect is
A4.3cms−1B5.3cms−1C6.3cms−1D7.3cms−1A block mass m moves on a horizontal circle against the wall of a cylinderical room of radius R. The floor of the room, on which the block moves, is smooth but the friction coefficient between the wall and the block is μ. The block is given an initial speed V0. the power developed by the resultant force acting on the block as a function of distance travelled s is
Aμm30Re−3sμBμmV30Re−3μsRCμmV30RDμmV30Re−3sRA block of mass m is projected on a smooth horizontal circular track with velocity v what is the average normal force exered by the circular walls on the block during motion A to B?
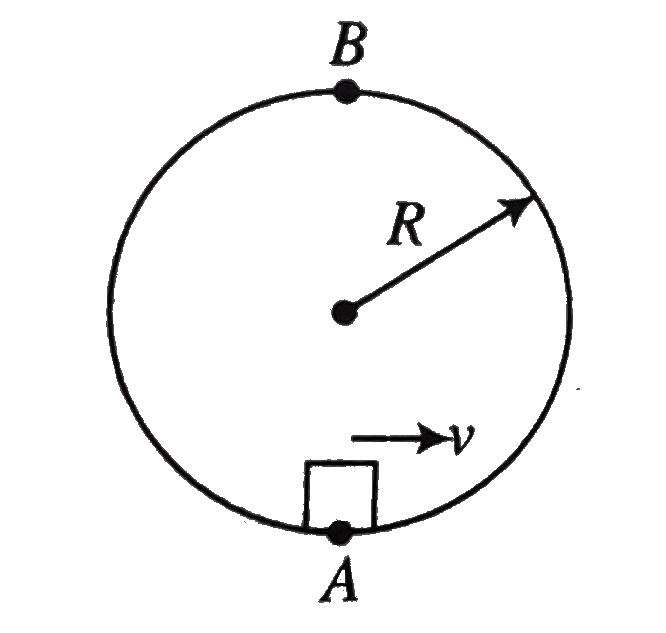 Amv2RBmv2πRC2mv2RD2mv2πR
Amv2RBmv2πRC2mv2RD2mv2πR
A block os mass m moves on as horizontal circle against the wall of a cylindrical room of radius R. The floor of the room onwhich the block moves is smoth but the friction coefficient between the wall and the block is μ. The block is given an initial speed v0. As a function of the speed v write a. the normal force by the wall on the block. b. thefrictional force by the wall and c. the tangential acceleration of the block. d. Integrate the tangential acceleration (dvdt=vdvds) to obtain the speed of the block after one revoluton.
View SolutionAn insect trapped in a circular groove of radius, 12 cm moves along the groove steadily and completes 7 revolutions in 100s. What is the angular speed and the linear speed of the motion ?
View SolutionThe ball of mas m moves with speed v againest a smooth , fixed vertical circular groove of radius R kept on smooth horizontal surface find the
a. normal reaction of the floor or the ball.
b. normal reaction of the vertical wall on the ball.
View SolutionA block of mass m is pressed against a wall which is moving with an acceleration a as shown in figure If the block is pulled at an angle θ with downward vertical by a force F and it does not slide relative to the wall . Find the
a. friction force between the block and wall
b.inimum magnitude of F so as to cayse a relative sliding between the block and wall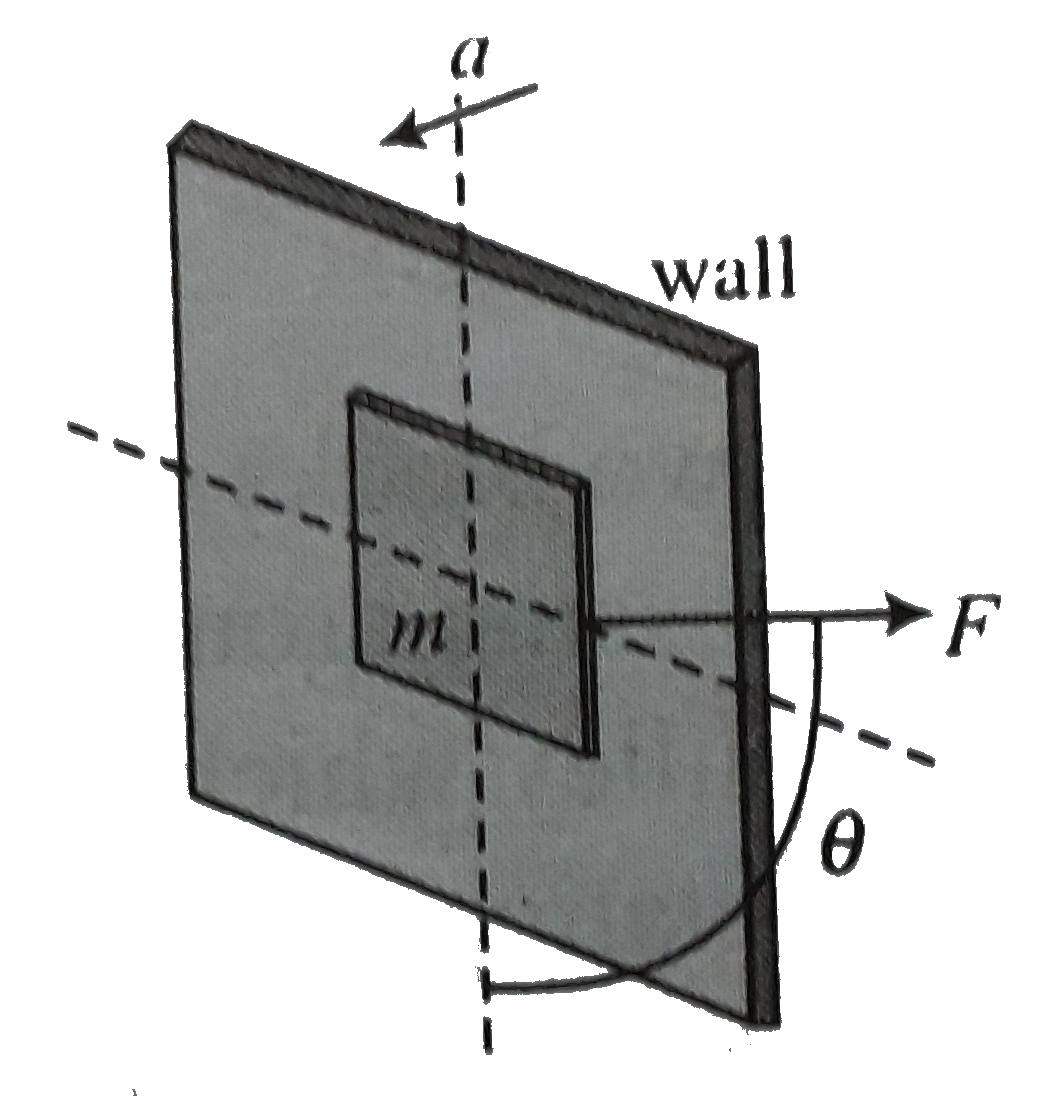
View SolutionAn Insect trapped in a circular groove of radius 12 cm moves along the groove steadily and completes 7 revolutions in 100 séc. The linear speed of the insect is
View Solution
