Two blocks ( m = 0.5 kg and M = 4.5 kg) are arranged on a horizontal frictionless table as shown in figure. The coefficient of static friction between the two blocks is 37. Then the maximum horizontal force that can be applied on the larger block move together is _____________ N. ( Round off to the Nearest Integer ) [Take as 9.8ms−2 ]
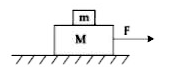
Step by step video & image solution for Two blocks ( m = 0.5 kg and M = 4.5 kg) are arranged on a horizontal frictionless table as shown in figure. The coefficient of static friction between the two blocks is (3)/( 7). Then the maximum horizontal force that can be applied on the larger block move together is "_____________" N. ( Round off to the Nearest Integer ) [Take as 9.8 ms^(-2) ] by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS SECTION A60videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS SECTION B30videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - PHYSICS (SECTION A)60videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions473videos
JEE MAIN
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question492videos
JEE MAIN 2022
Similar Questions
The coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is N. (take g=10ms−2)
 View Solution
View SolutionThe coefficient of static friction between the two blocks shown in figure is μ and the table is smooth. What maximum horizontal forced F can be applied to he block of mass M so that the block move together?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Coefficient of static friction between the two blocks in Fig. 7.124 is μ and the table is frictionless . Maximum horizontal force which can be applied on the lower such that the blocks move together , is :
 Aμm1gBμm2gCμ(m1−m2)gDμ(m1+m2)g
Aμm1gBμm2gCμ(m1−m2)gDμ(m1+m2)g - Question 2 - Select One
The two blocks, m= 10 kg and M = 50 kg are free to move as shown. The coefficient of static friction between the blocks is 0.5 and there is no friction between M and the ground. A minimum horizontal force F is applied to hold m against M that is equal to -
 A100 NB50 NC240 ND180 N
A100 NB50 NC240 ND180 N - Question 3 - Select One
Two blocks of 2 kg and I kg are in contact on a frictionless table. If a force of 3 N is applied on 2 kg block, then the force of contact between the two blocks will be
 A0 NB1 NC2 ND3 N
A0 NB1 NC2 ND3 N
Two blocks of mass m = 1 kg and M = 2 kg are in contact on a frictionless table. A horizontal force F(= 3N) is applied to m. The force of contact between the blocks, will be-
View SolutionThe coefficient of static friction between a wooden block of mass 0.5 kg and a vertical rough wall is 0.2. The magnitude of horizontal force that should be applied on the block to keep it adhere to the wall will be ____N.
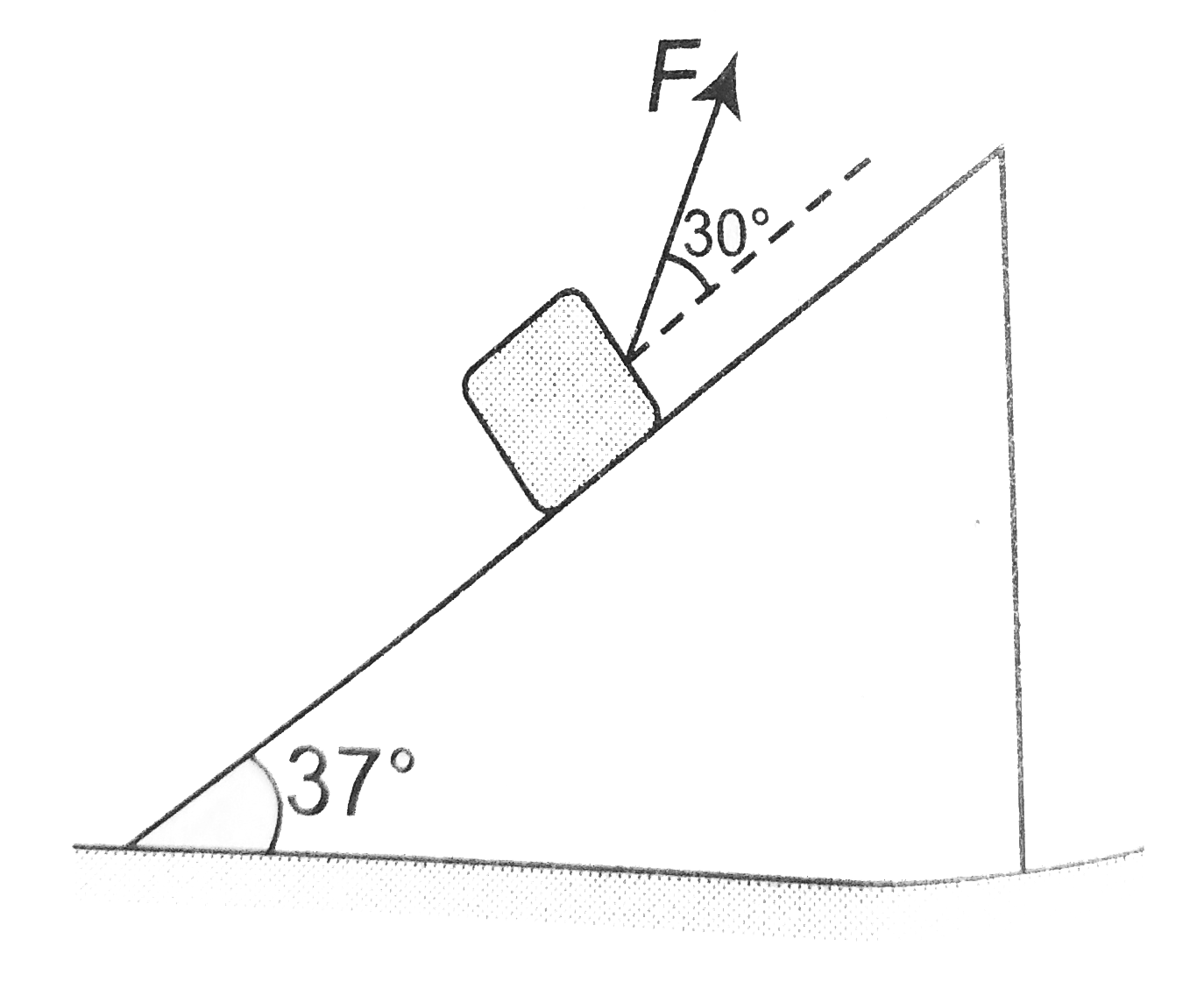
View SolutionA block of mass m=4kg is placed oner a rough inclined plane as shown in figure. The coefficient of friction between the block and the plane is μ=0.5 . A force F=10N is applied on the block at an angle of 30∘ .
 View Solution
View SolutionIn the arrangement shown in figure the wall is smooth and friction coefficient between the blocks is μ=0.1. A horizontal force F=1000N is applied on the 2kg block. The wrong statement is :
 View Solution
View SolutionA block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, then the magnitude of the frictional force acting on the block is
View Solution

