Two objects are moving along the same straight line. They cross a point A With an acceleration a, 2a and velocity 2u, u at time t=0. The distance moved by the object when one overtakes the
6u2a
2u2a
4u2a
8u2a
The correct Answer is:A
To solve the problem of two objects moving along the same straight line and determining the distance at which one overtakes the other, we can follow these steps:
Step 1: Identify the initial conditions
- Object 1 has:
- Initial velocity u1=2u
- Acceleration a1=a
- Object 2 has:
- Initial velocity u2=u
- Acceleration a2=2a
Step 2: Write the equations of motion for both objects
Using the equation of motion S=ut+12at2:
- For Object 1:
S1=u1t+12a1t2=2ut+12at2
- For Object 2:
S2=u2t+12a2t2=ut+12(2a)t2=ut+at2
Step 3: Set the distances equal to find the time of overtaking
Since the two objects will overtake each other at the same distance, we set S1=S2:
2ut+12at2=ut+at2
Step 4: Rearrange the equation
Rearranging gives:
2ut−ut+12at2−at2=0
ut−12at2=0
Step 5: Factor out common terms
Factoring out t:
t(u−12at)=0
This gives us two solutions: t=0 (initial condition) or u−12at=0.
Step 6: Solve for time t
Setting the second factor to zero:
u=12at⟹t=2ua
Step 7: Substitute t back to find the distance
Now we can substitute t=2ua back into either distance equation. Let's use S1:
S1=2u(2ua)+12a(2ua)2
S1=4u2a+12a⋅4u2a2
S1=4u2a+2u2a=6u2a
Final Answer
The distance moved by the object when one overtakes the other is:
6u2a
- Object 1 has:
- Initial velocity u1=2u
- Acceleration a1=a
- Object 2 has:
- Initial velocity u2=u
- Acceleration a2=2a
Using the equation of motion S=ut+12at2:
S1=u1t+12a1t2=2ut+12at2
S2=u2t+12a2t2=ut+12(2a)t2=ut+at2
Since the two objects will overtake each other at the same distance, we set S1=S2:
2ut+12at2=ut+at2
Rearranging gives:
2ut−ut+12at2−at2=0
ut−12at2=0
Factoring out t:
t(u−12at)=0
This gives us two solutions: t=0 (initial condition) or u−12at=0.
Setting the second factor to zero:
u=12at⟹t=2ua
Now we can substitute t=2ua back into either distance equation. Let's use S1:
S1=2u(2ua)+12a(2ua)2
S1=4u2a+12a⋅4u2a2
S1=4u2a+2u2a=6u2a
The distance moved by the object when one overtakes the other is:
6u2a
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Subjective50videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - More Than One Correct6videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Assertion And Reason12videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
Average velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionAverage velocity of a particle moving in a straight line, with constant acceleration a and initial velocity u in first t seconds is.
View SolutionA particle moving along a straight line with initial velocity u and acceleration a continues its motion for n seconds. What is the distance covered by it in the last nth second ?
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
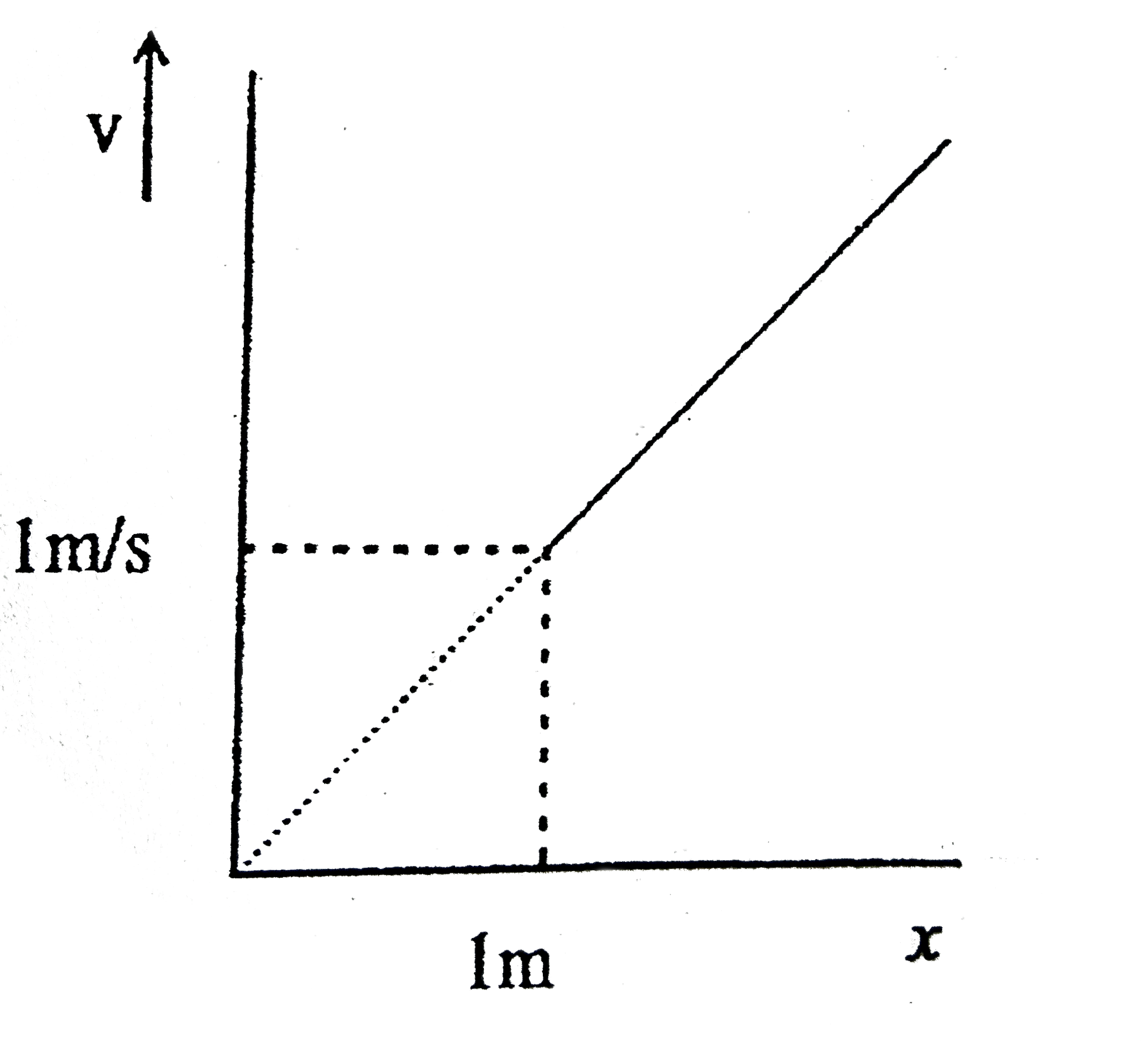 View Solution
View SolutionTwo particles start moving from the same point along the same straight line. The first moves with constant velocity v and the second with constant acceleration a. During the time that elapses before the sound catches the first, the greatest distance between the particle is.
View Solution
For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as
v=u+at, (u=initial velocity)
Draw the velocity-time graph of the particle in following situations.
(i) Velocity is decresing with time (i.e., acceleration in negative)
(ii) Initial velocity is negative but acceleration is positiveView SolutionA body moving in a straight line with constant acceleration covers distances a and b in successive equal time interval of t. The acceleration of the body is
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View SolutionStatement-I : A particle moves in a straight line with constant acceleration. The average velocity of this particle cannot be zero in any time interval.
Statement-II : For a particle moving in straight line with constant acceleration, the average velocity in a time interval is u+v2, where u and v are initial and final velocity of the particle of the given time interval.View SolutionThe velocity-time graph of a particle moving along a straight line is shown is . The rate of acceleration and deceleration is constant and it is equal to 5ms−2. If the a average velocity during the motion is 20ms−1, Then
 .
.
The value of t is.View Solution

