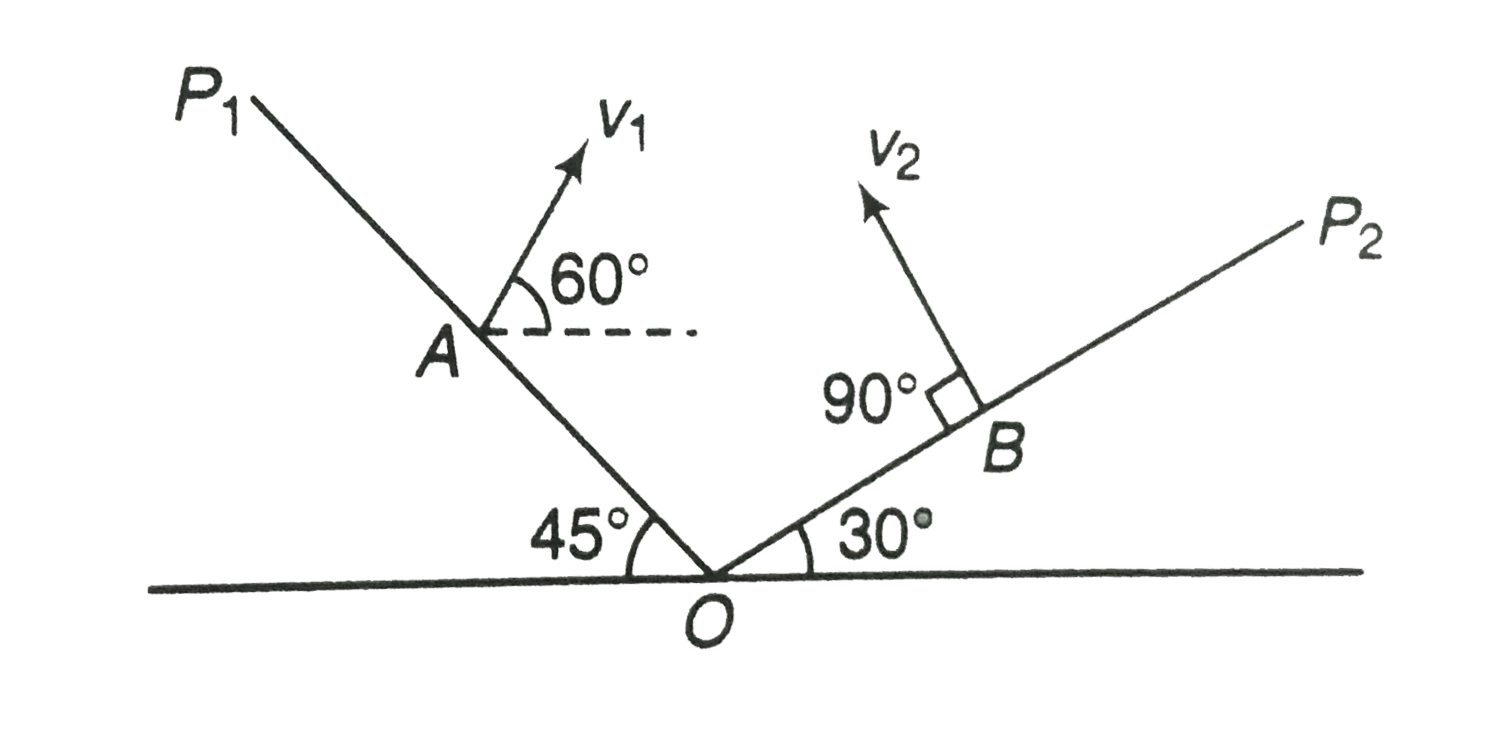
A particle is projected from an inclined plane OP1 from A with velocity v1=8ms−1 at an angle 60∘ with horizontal. An another particle is projected at the same instant from B with velocity v2=16ms−1 and perpendicular to the plane OP2 as shown in figure. After time 10(√3) s there separation was minimum and found to be 70m. Then find distance AB.
The correct Answer is:B
|v21x|=(v1+v2)cos60∘=12m/s
∣∣v21y∣∣=(v2−v1)sin60∘=4(√3)m/s
∴v21=√(12)2+(4√3)2=(√192)m/s

BC=(v21)t=240m
AC=70m
Hence, AB=√(240)2+(70)2=250m.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct8videos
PROJECTILE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery32videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
Similar Questions
A ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is
 View Solution
View SolutionA particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA particle is projected with a velocity of 20ms−1 at an angle of 60∘ to the horizontal. The particle hits the horizontal plane again during its journey. What will be the time of impact ?
View SolutionA particle is projected with velocity 20ms−1 at angle 60∘ with horizontal . The radius of curvature of trajectory , at the instant when velocity of projectile become perpendicular to velocity of projection is , (g=10ms−1)
View SolutionA particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionA body is projected down from height of 60 m with a velocity 10ms−1 at angle 30∘ to horizontal. The time of flight of the body is [g=10ms−2]
View SolutionA particle is projected horizontally form a tower with velocity 10ms−1. Taking g=10ms−2. Match the following two columns at time t = 1s.
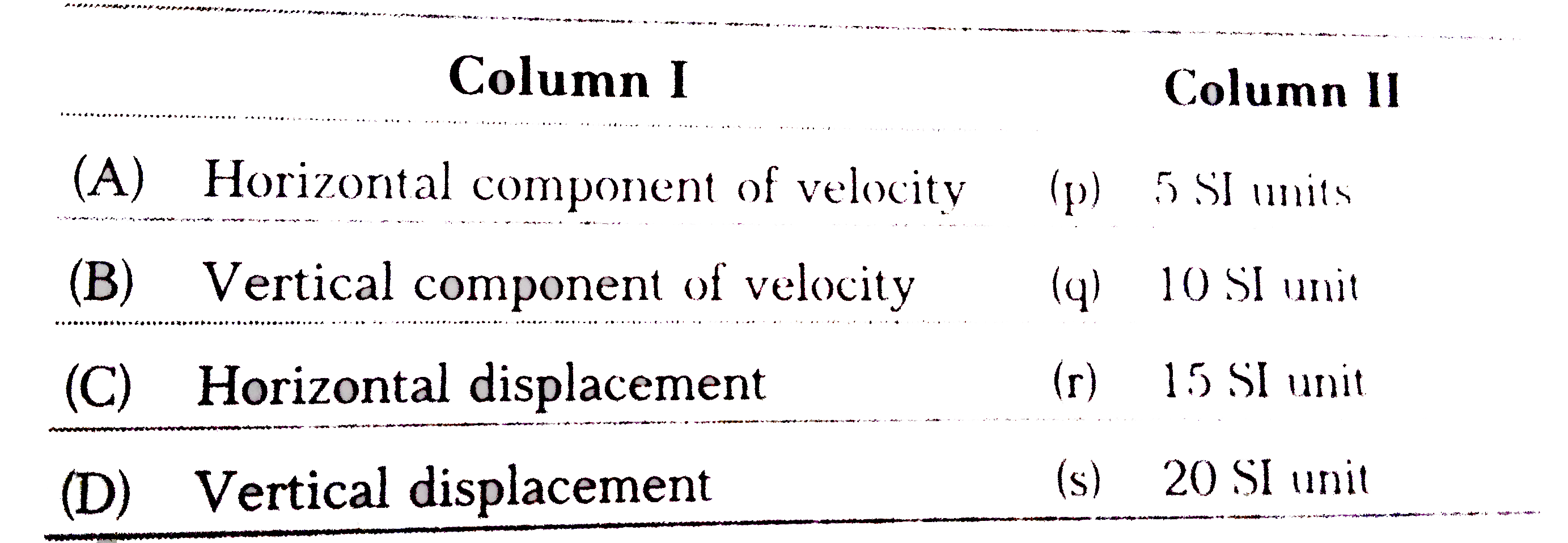 View Solution
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time
 View Solution
View Solution

