Question

A partical of mass $1kg$ rests on rought contact with a plane inclined at ${30}^{\circ }$ to the horizontal and is just about to slip, Find the coefficient of friction between the plane and the particle.

Explanation

To find the coefficient of friction between the plane and the particle, we can follow these steps:

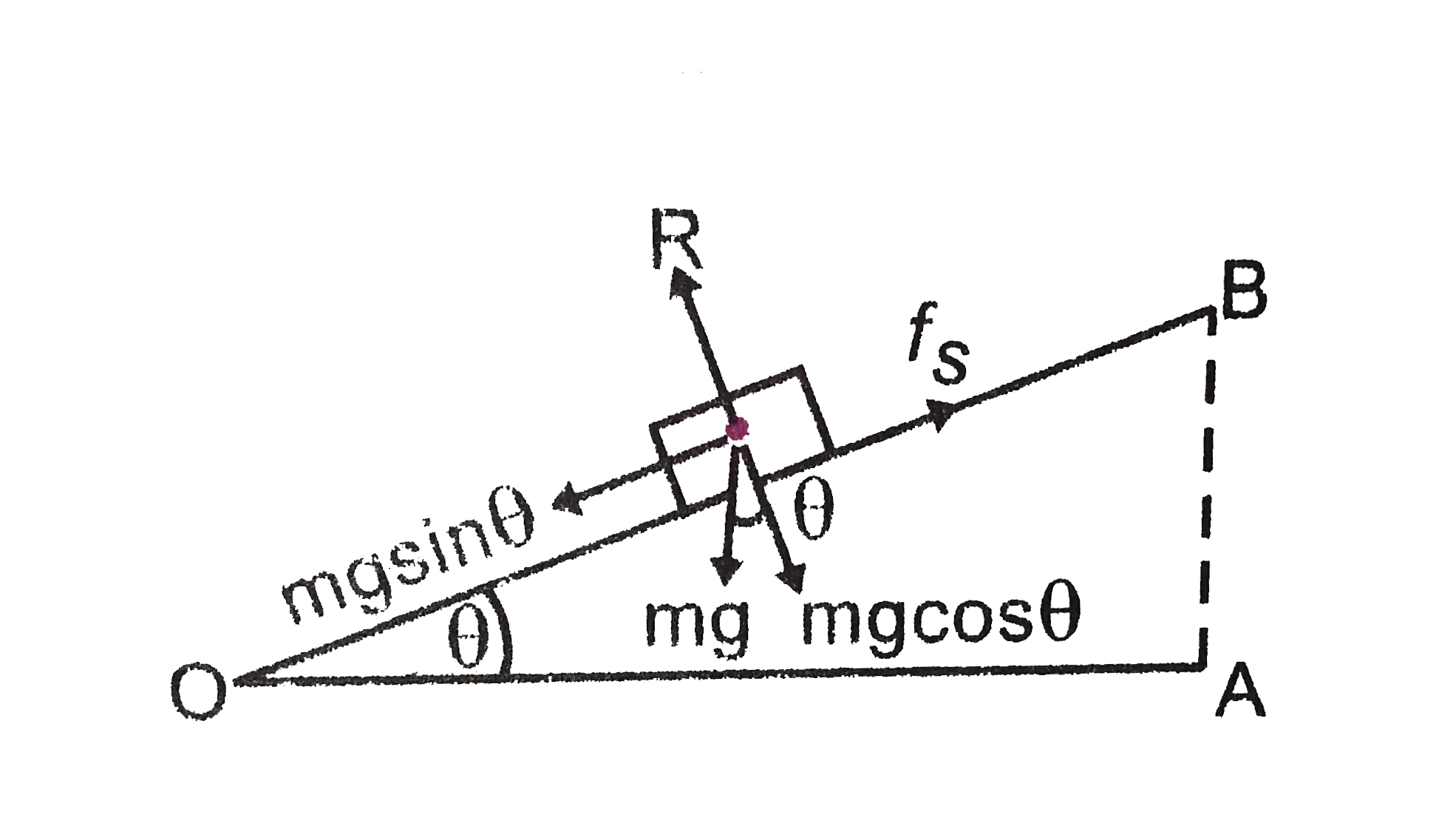
Step 1: Identify the forces acting on the particle
The forces acting on the particle include:
- The weight of the particle (W = mg)
- The normal force (N)
- The frictional force (f)

Given:
- Mass of the particle (m) = 1 kg
- Angle of inclination (θ) = 30°

Step 2: Calculate the weight of the particle
The weight (W) of the particle can be calculated using the formula:
\( W = mg \)
Where \( g \) (acceleration due to gravity) is approximately \( 9.81 \, \text{m/s}^2 \).

So,
\( W = 1 \, \text{kg} \times 9.81 \, \text{m/s}^2 = 9.81 \, \text{N} \)

Step 3: Resolve the weight into components
The weight of the particle can be resolved into two components:
1. Perpendicular to the incline: \( W_{\perp} = mg \cos \theta \)
2. Parallel to the incline: \( W_{\parallel} = mg \sin \theta \)

Calculating these components:
- \( W_{\perp} = 9.81 \, \text{N} \cdot \cos(30^\circ) \)
- \( W_{\parallel} = 9.81 \, \text{N} \cdot \sin(30^\circ) \)

Using \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \) and \( \sin(30^\circ) = \frac{1}{2} \):
- \( W_{\perp} = 9.81 \cdot \frac{\sqrt{3}}{2} \approx 8.49 \, \text{N} \)
- \( W_{\parallel} = 9.81 \cdot \frac{1}{2} = 4.905 \, \text{N} \)

Step 4: Determine the normal force
The normal force (N) is equal to the perpendicular component of the weight:
\( N = W_{\perp} = mg \cos \theta \)
Thus,
\( N = 8.49 \, \text{N} \)

Step 5: Set up the equation for limiting friction
Since the particle is just about to slip, the limiting friction (f) is equal to the parallel component of the weight:
\( f = W_{\parallel} = mg \sin \theta \)

Step 6: Relate limiting friction to the coefficient of friction
The limiting friction can also be expressed in terms of the coefficient of friction (μ) and the normal force (N):
\( f = \mu N \)

Setting the two expressions for friction equal gives:
\( mg \sin \theta = \mu (mg \cos \theta) \)

Step 7: Solve for the coefficient of friction (μ)
Dividing both sides by \( mg \cos \theta \):
\( \mu = \frac{mg \sin \theta}{mg \cos \theta} \)
This simplifies to:
\( \mu = \frac{\sin \theta}{\cos \theta} = \tan \theta \)

Step 8: Substitute the angle
Now substituting \( \theta = 30^\circ \):
\( \mu = \tan(30^\circ) \)

Using the known value:
\( \tan(30^\circ) = \frac{1}{\sqrt{3}} \)

Final Answer
Thus, the coefficient of friction (μ) is:
\( \mu = \frac{1}{\sqrt{3}} \)

---