In the arrangement shown in figure the mass of the ball is times as that of the rod. The length of the rod is the masses of the pulleys and the threads as well as the friction, are negligible. The ball is set on the same level as the lower end of the rod and then released. How soon will the ball be opposite the upper end of the rod?

From constraint relation we can see that the acceleration of the rod is double then that of the acceleration of the ball .If ball is going up with an acceleration , rod will be coming down with the acceleration , thus the relative acceleration of the ball with respect to rod is in upward direction. If it takes time seconds to reach the upper end of the rod, we have
...(i)
Let mass of ball be and that of rod is the dynamic of these are
For rod ...(i)
For rod ...(ii)
Substituting and solving Eqs (ii) and (iii), we get
From Eq (i), we have

Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.1
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.2
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Solved Examples
15 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
In the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
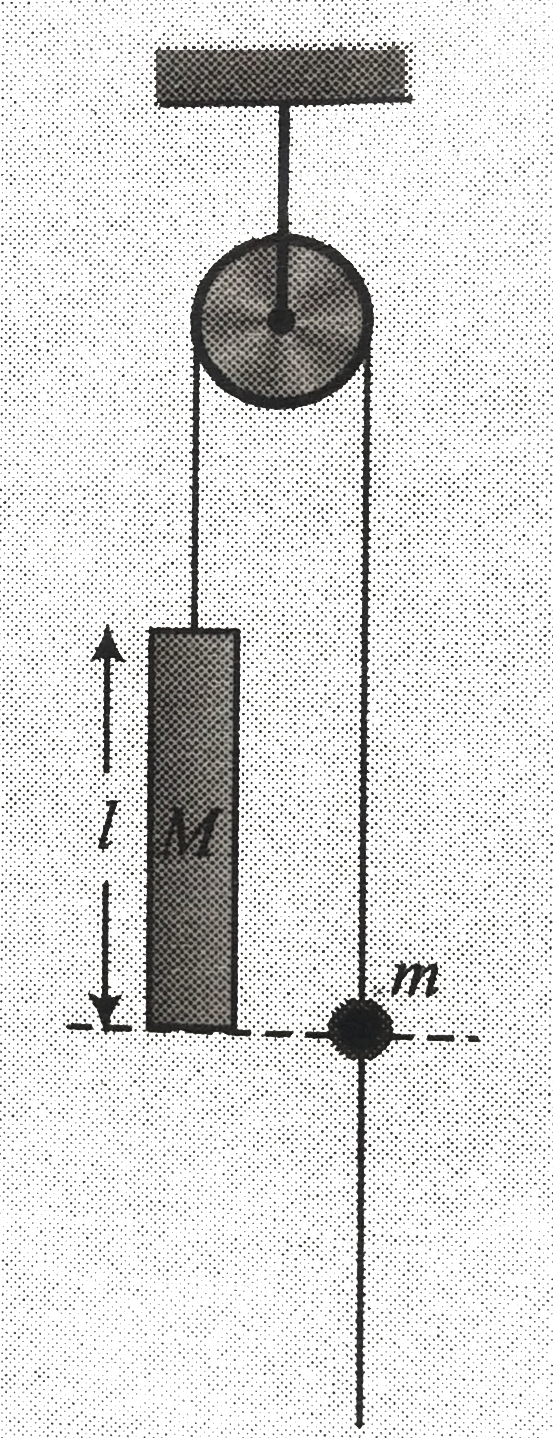
View SolutionIn the arrangement shown in figure the mass of the ball is η times as that of the rod. The length of the rod is L the masses of the pulleys and the threads as well as the friction, are negligible. The ball is set on the same level as the lower end of the rod and then released. How soon will the ball be opposite the upper end of the rod?

View SolutionFind the accelerations of rod A and wedge B in the arrangement shown in figure if the ratio of the mass of the wedge to that of the rod equals η, and the friction between all contact surfaces is negligible.

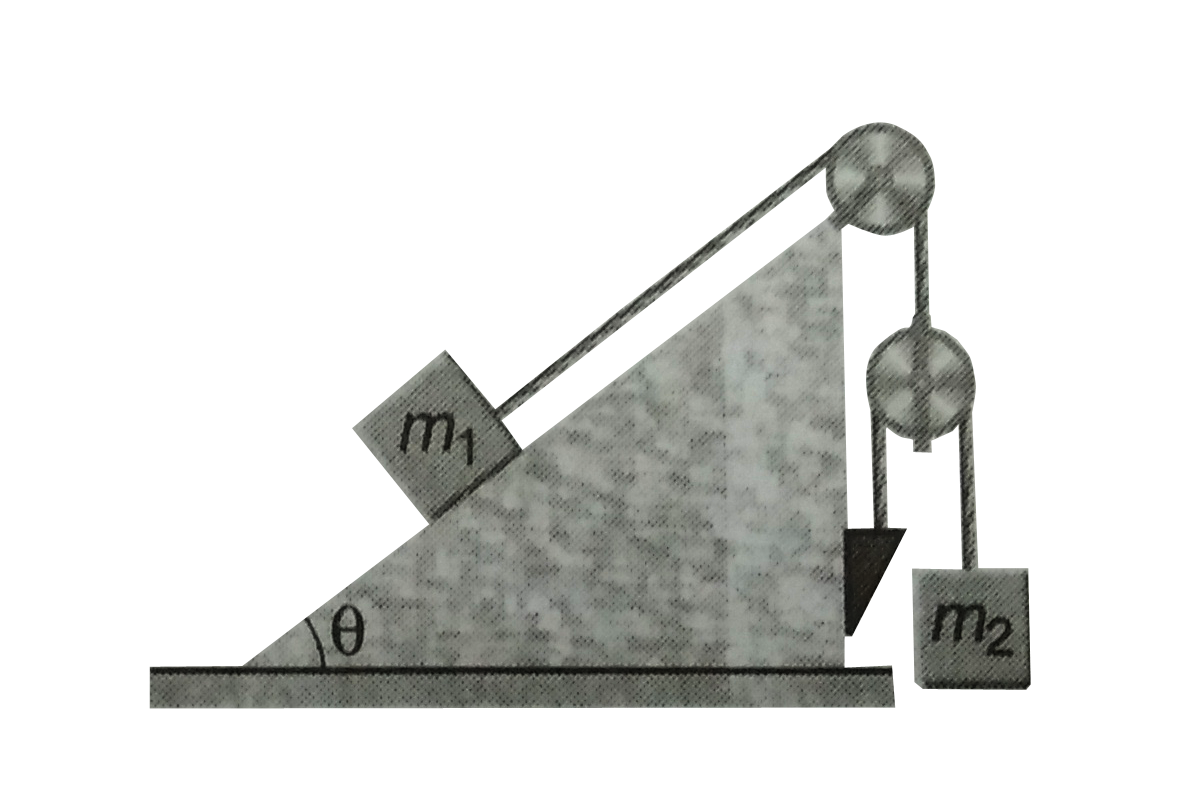
View SolutionFind the acceleration of the body of mass m2 in the arrangement shown in figure. If the massm2 is η time the mass m1 and the angle that the inclined plane forms with the horizontal is equal to θ. The masses of the pulley and threads, as well as the friction, are assumed to be negligible.
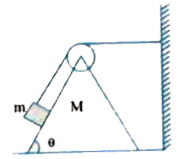
View SolutionA block of mass m is arranged on the wedge as shown in figure . The wedge angle is θ. If the masses of pulley and thread and negligible and friction is absent , find the acceleration of the wedge
View SolutionIn the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be

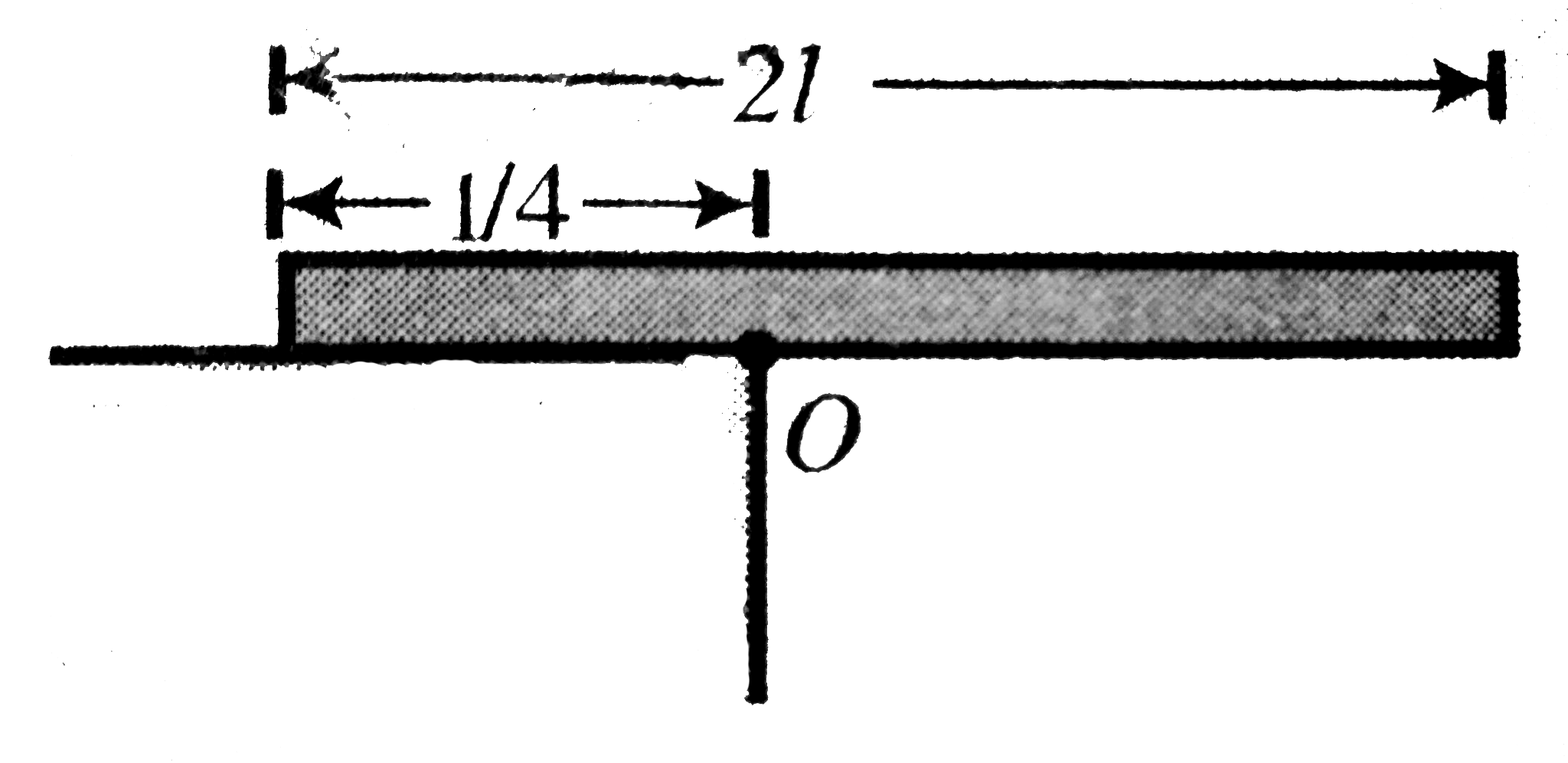
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.
View SolutionUniform rod AB is hinged at the end A in a horizontal position as shown in the figure ( the hinge is frictionless that is , it does not exert any friction force on the rod ). The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless . Masses of the block and the rod are same and are equal to 'm'.
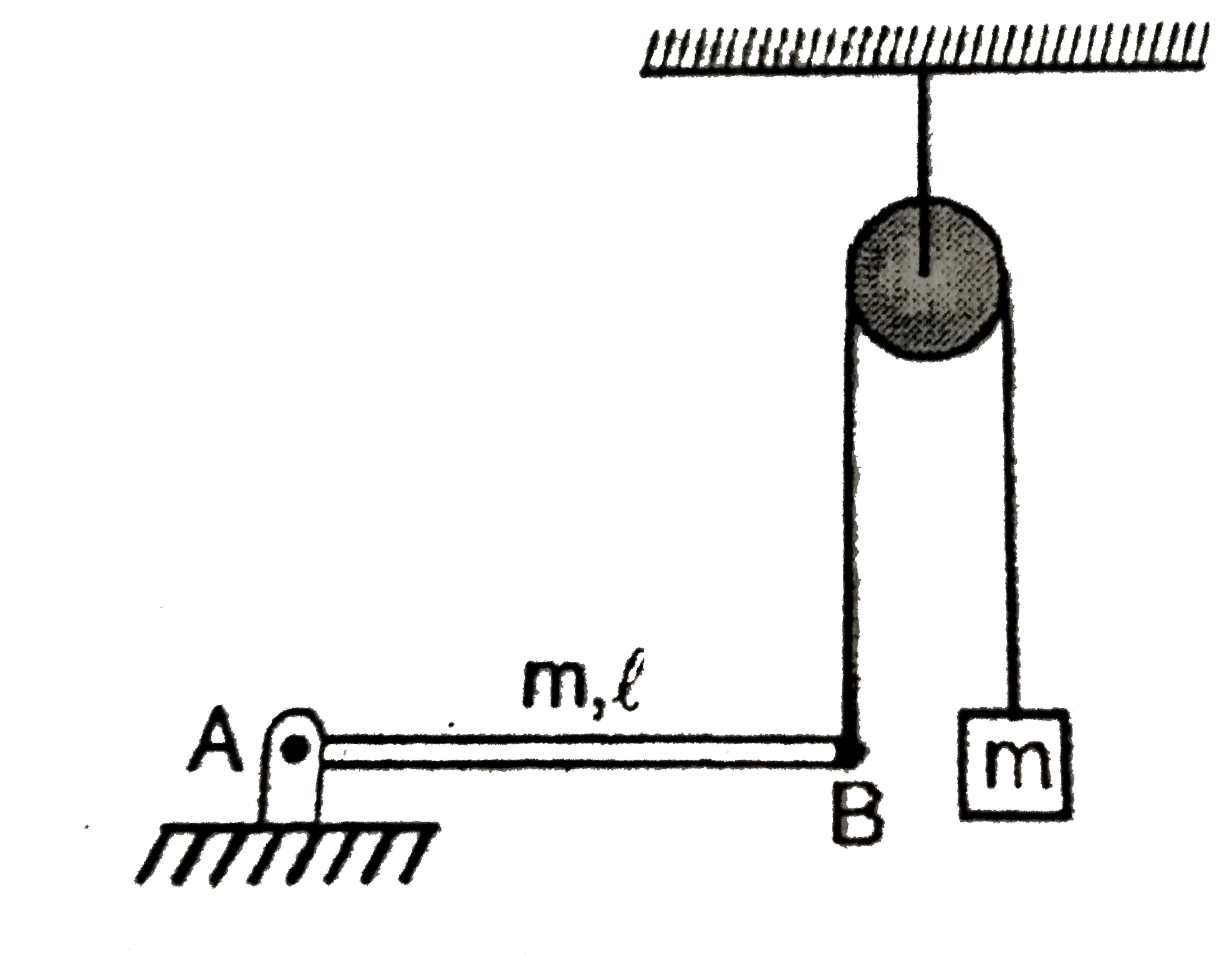
Then just after released of block from this position, the angular acceleration of the rod is
View SolutionUniform rod AB is hinged at the end A in a horizontal position as shown in the figure ( the hinge is frictionless that is , it does not exert any friction force on the rod ). The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless . Masses of the block and the rod are same and are equal to 'm'.
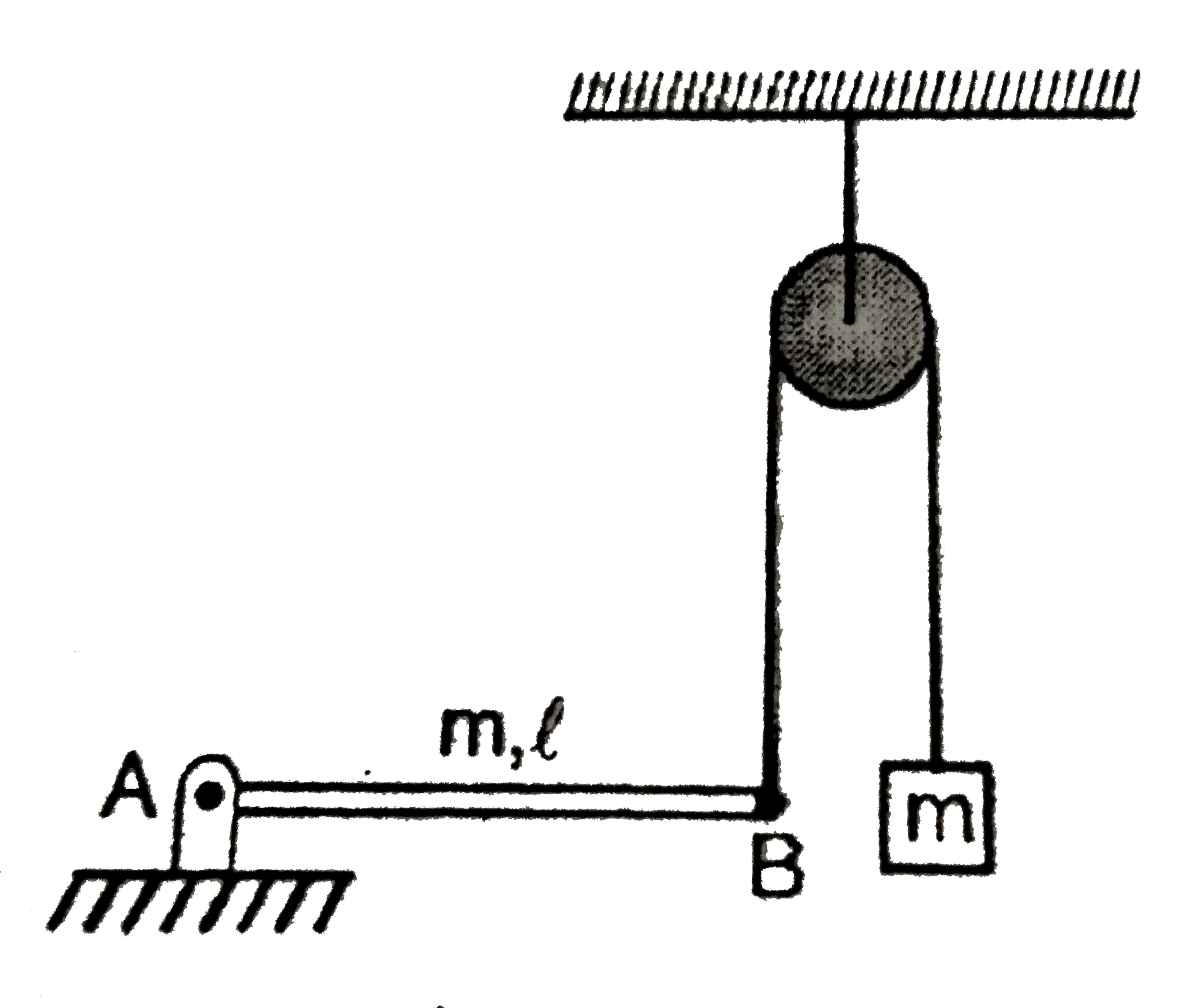
Then just after release of block from this position, the tension in the thread is
View SolutionUniform rod AB is hinged at the end A in a horizontal position as shown in the figure ( the hinge is frictionless that is , it does not exert any friction force on the rod ). The other end of the rod is connected to a block through a massless string as shown. The pulley is smooth and massless . Masses of the block and the rod are same and are equal to 'm'.
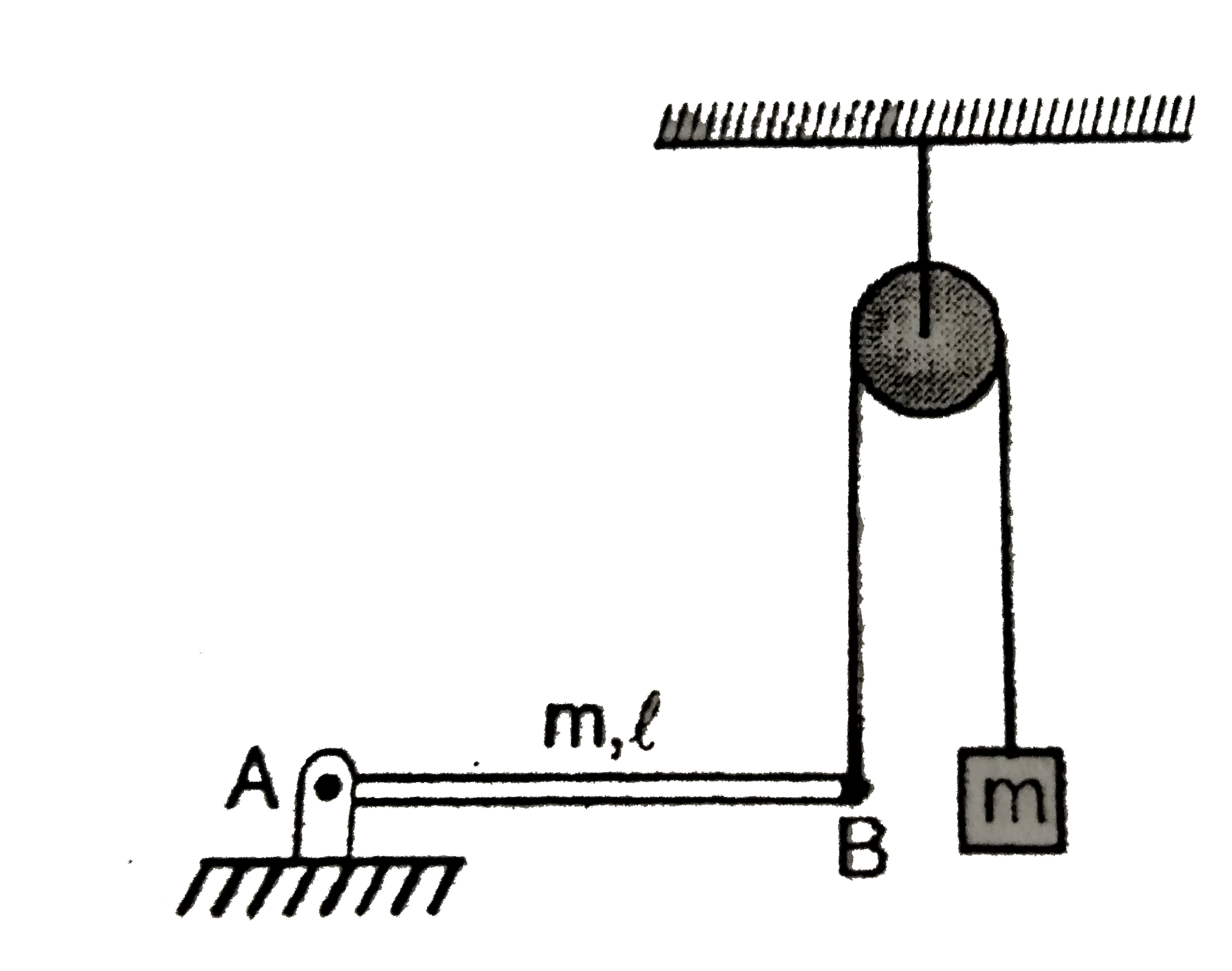
Then just after release of block from this position, the magnitude of reaction exerted by hinge on the rod is
View Solution
