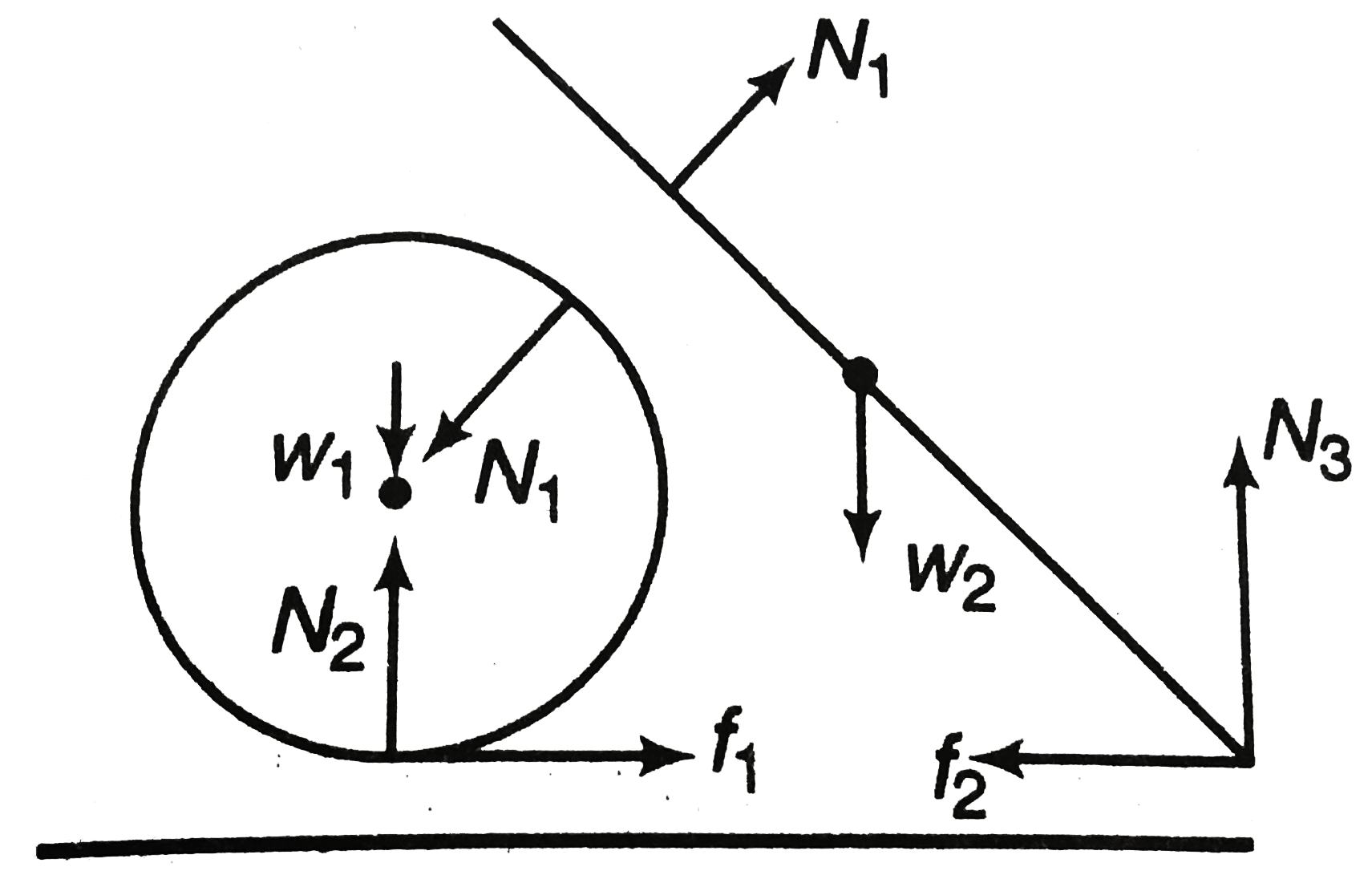
The diagram shows a rough plank resting on a cylinder with one and of the plank on rough ground. Negtect friction between plank and cylinder. Draw digrams to show
(a) the force acting on the plank,
(b)the force acting on the cylinder.

w1= weight of cylinder
w2= weight of plank
N1= normal reation between cyclinder and plank
N2= normal reation on cyclinder from ground
N3= normal reation on plank from ground f1= force of friction on cyclinder from ground f2= force of friction on plank from ground
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.2
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.3
8 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Miscellaneous Examples
9 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
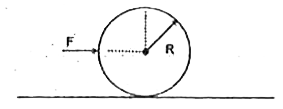
A force F is applied horizontally on a cylinder in the line of centre as shown in the figure. The cylinder is on a rough surface of coefficient of fricition μ. The direction of the friction force acting on the cylinder will be
View SolutionA girl finds herself stuck with her back to the wall of a cylinder rotating about its axis. Which diagram correctly shows the forces acting on her?

View Solution
Knowledge Check
In the question number 89, the force of friction acting on the cylinder is
A2/3 Mg sinθB1/3 Mg sinθC2/5 Mg sinθD2/7 Mg sinθ
In the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View SolutionA plank of mass 2kg and length 1m is placed on horizontal floor.A small block of mass 1kg is placed on top of the plank , at its right extreme end .The coefficient of friction between plank and floor is 0.5 and that between plank and block is 0.2 . If a horizontal force =30N starts acting on the plank to the right ,the time after which the block will fall off the plank is (g=10ms−2)
View SolutionThe figure shows a spool placed at rest on a horizontal rough surface. A tightly wound string on the inner cylinder is pulled horizontally with a force F. identify the correct alternative related to the friction f acting on the spool
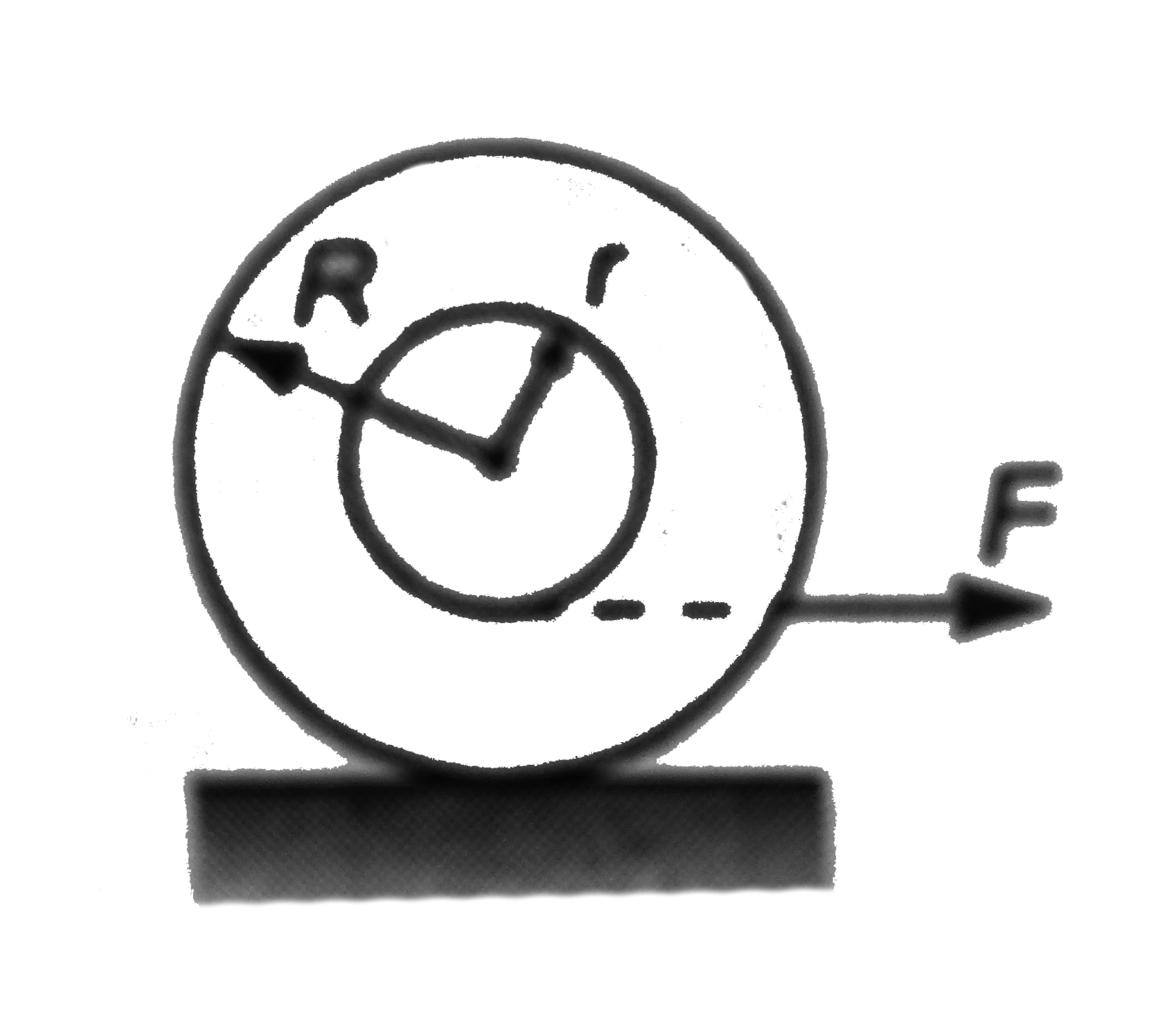
View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
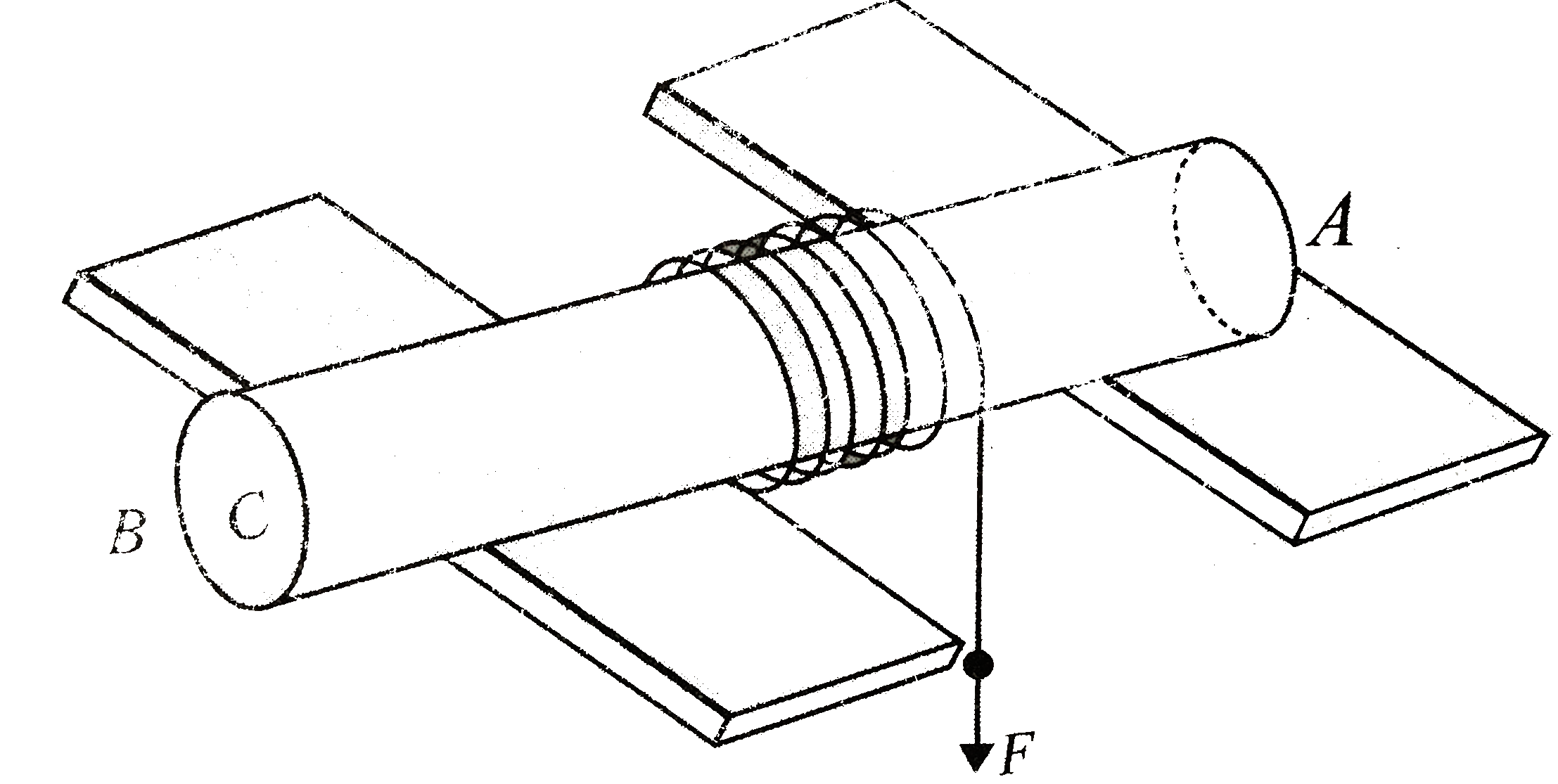
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionA plank A of mass M rests on a smooth horizontal surface over which it can move without friction A cabe B of mass m lies on the plank at one edge .The coefficient of friction between the plank and the cube is μ The size of cube is very small in comparison to the plank.

At what force F applied to the plank in the horizontal direction will be cube begin to slide towards the other end of the plank?
View Solution
A cylinder of radius R is to roll without slipping between two planks as shown in the figure. Then
View SolutionA plank of mass M, is placed on a smooth surface over which a cylinder of mass m(=M) annd radius R=1m is placed as shown in figure. Now the plane is pulled towards the right wilth an external force F(=2Mg). If the cyinder does not slip over the surfcace of the plank, find the linear acceleration of he plank and the cylinder and the angular acceleration of the cylinder. (Take g=10ms2)

View Solution
