A plank of mass 2kg and length 1m is placed on horizontal floor.A small block of mass 1kg is placed on top of the plank , at its right extreme end .The coefficient of friction between plank and floor is 0.5 and that between plank and block is 0.2 . If a horizontal force =30N starts acting on the plank to the right ,the time after which the block will fall off the plank is (g=10ms−2)
(23)s
1.5s
0.75s
(43)s
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on both the plank and the block, calculate their accelerations, and then determine the time it takes for the block to fall off the plank.
Step 1: Identify the forces acting on the block and the plank
- The plank has a mass of m1=2kg.
- The block has a mass of m2=1kg.
- The horizontal force acting on the plank is F=30N.
- The coefficient of friction between the plank and the block is μ1=0.2.
- The coefficient of friction between the plank and the floor is μ2=0.5.
- The gravitational acceleration is g=10m/s2.
Step 2: Calculate the maximum frictional force between the block and the plank
The normal force N1 acting on the block due to gravity is:
N1=m2⋅g=1kg⋅10m/s2=10N
The maximum frictional force F1,max between the block and the plank is given by:
F1,max=μ1⋅N1=0.2⋅10N=2N
Step 3: Calculate the maximum frictional force between the plank and the ground
The normal force N2 acting on the plank is:
N2=(m1+m2)⋅g=(2kg+1kg)⋅10m/s2=30N
The maximum frictional force F2,max between the plank and the ground is:
F2,max=μ2⋅N2=0.5⋅30N=15N
Step 4: Determine the acceleration of the plank
The net force acting on the plank is:
Fnet=F−F2,friction=30N−F2,friction−F1,friction
Where F2,friction is the friction force opposing the motion of the plank. The maximum friction force that can act between the block and the plank is 2N, so:
Fnet=30N−15N−2N=13N
The acceleration a2 of the plank is:
a2=Fnetm1=13N2kg=6.5m/s2
Step 5: Determine the acceleration of the block
The block will accelerate due to the frictional force acting on it, which is the maximum frictional force F1,max:
a1=F1,maxm2=2N1kg=2m/s2
Step 6: Calculate the relative acceleration
The relative acceleration arelative between the plank and the block is:
arelative=a2−a1=6.5m/s2−2m/s2=4.5m/s2
Step 7: Calculate the time taken for the block to fall off the plank
The distance s that the block needs to travel to fall off the plank is equal to the length of the plank, which is 1m. Using the equation of motion:
s=ut+12arelativet2
Since the initial velocity u=0:
1=0+12⋅4.5⋅t2
1=2.25t2
t2=12.25=49
t=23s
Final Answer
The time after which the block will fall off the plank is 23 seconds.
- The plank has a mass of m1=2kg.
- The block has a mass of m2=1kg.
- The horizontal force acting on the plank is F=30N.
- The coefficient of friction between the plank and the block is μ1=0.2.
- The coefficient of friction between the plank and the floor is μ2=0.5.
- The gravitational acceleration is g=10m/s2.
The normal force N1 acting on the block due to gravity is:
N1=m2⋅g=1kg⋅10m/s2=10N
The maximum frictional force F1,max between the block and the plank is given by:
F1,max=μ1⋅N1=0.2⋅10N=2N
The normal force N2 acting on the plank is:
N2=(m1+m2)⋅g=(2kg+1kg)⋅10m/s2=30N
The maximum frictional force F2,max between the plank and the ground is:
F2,max=μ2⋅N2=0.5⋅30N=15N
The net force acting on the plank is:
Fnet=F−F2,friction=30N−F2,friction−F1,friction
Where F2,friction is the friction force opposing the motion of the plank. The maximum friction force that can act between the block and the plank is 2N, so:
Fnet=30N−15N−2N=13N
The acceleration a2 of the plank is:
a2=Fnetm1=13N2kg=6.5m/s2
The block will accelerate due to the frictional force acting on it, which is the maximum frictional force F1,max:
a1=F1,maxm2=2N1kg=2m/s2
The relative acceleration arelative between the plank and the block is:
arelative=a2−a1=6.5m/s2−2m/s2=4.5m/s2
The distance s that the block needs to travel to fall off the plank is equal to the length of the plank, which is 1m. Using the equation of motion:
s=ut+12arelativet2
Since the initial velocity u=0:
1=0+12⋅4.5⋅t2
1=2.25t2
t2=12.25=49
t=23s
The time after which the block will fall off the plank is 23 seconds.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Subjective Question
27 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Single Correct
90 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A man wants to slide down a block of mass m which is kept on a fixed inclined plane of inclination 30∘ as shown in the figure .Initially the block is not sliding .
To just start sliding the man pushed the block down the inclined with a force F. Now , the block starts accelerating. To move it downwards with conatant speed the man starts pulling the block with same force. Surface are such that ratio of maximum static friction to kinetic friction is 2 Now, answer the following questions.

What is the value of F?
View SolutionA small sphere is projected with a velocity of 3ms−1 in a direction 60∘ from the horizontal y - axis, on the smooth inclined plane (Fig. 5.197). The motion of sphere takes place in the x - y plane. Calculate the magnitude v of its velocity after 2s.
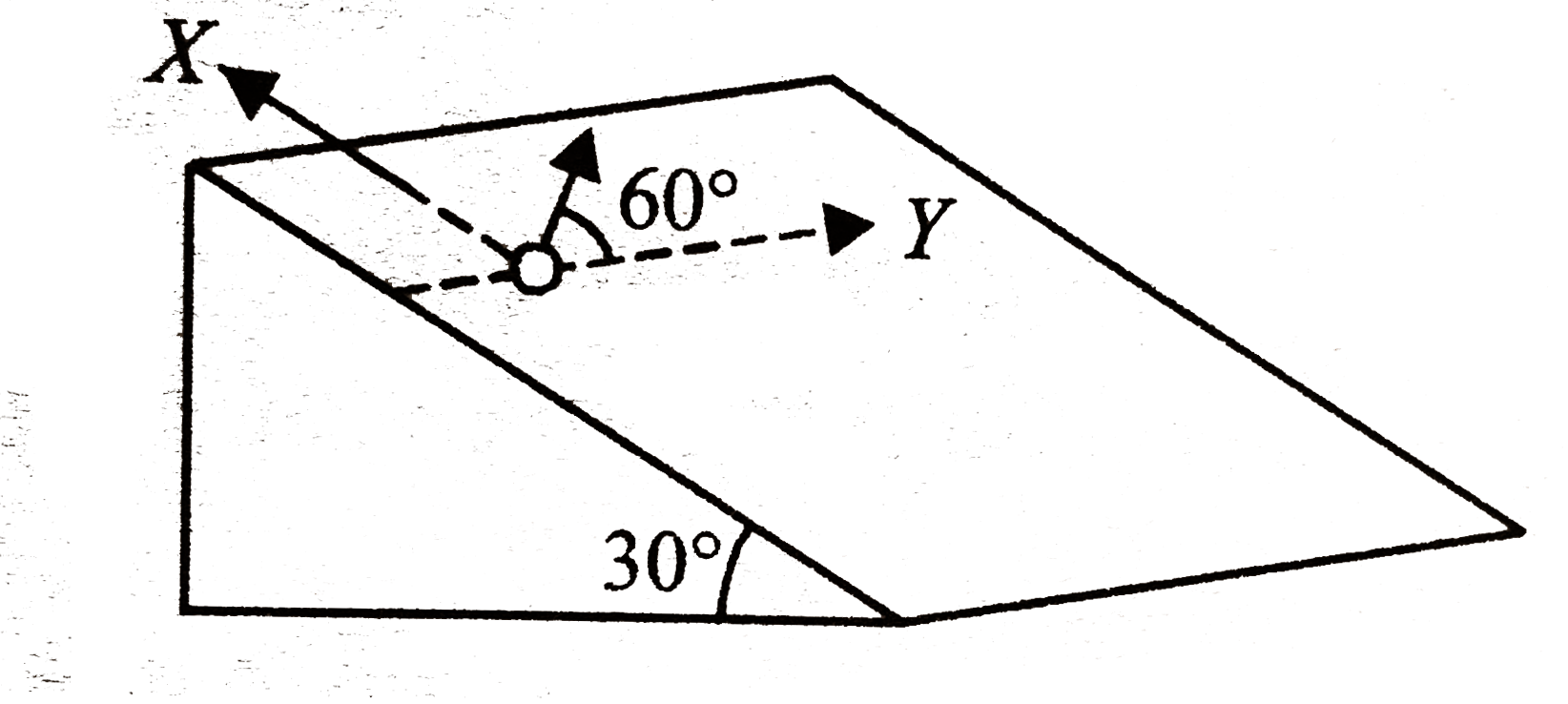 .
.
View SolutionThree equal weight A,B and C of mass 2kg each are hanging on a string passing over a fixed frictionless pulley as shown in the figure. The tension in the string connecting weights B and C is approximately

View SolutionA stone is dropped from a certain height which can reach the ground in 5s. It is stopped after 3s of its fall and then it is again released. The total time taken by the stone to reach the ground will be .
View SolutionTwo moles of helium gas undergo a cyclic process as shown in Fig. Assuming the gas to be ideal, calculate the following quantities in this process
(a) The net change in the heat energy
(b) The net work done
(c) The net change in internal energy
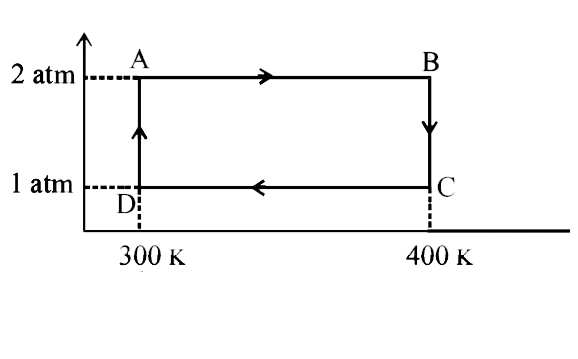
View SolutionFigure shown a small block A of mass m kept at the left end of a plank B of mass M = 2m and length l . The system can side on a horizontal rood. The system is started towards right with the initial velocity v . The friction coefficient between the rood and the plank is 1//2 and that between the plank and the block is 1//4 . Find (a) the time elapsed before the block separates from the plank (b) displacement of block and plank relative to ground till that moment.
View SolutionA plank of mass 2 kg and length 1 m is placed on horizontal floor.A small block of mass 1 kg is placed on top of the plank , at its right extreme end .The coefficient of friction between plank and floor is 0.5 and that between plank and block is 0.2 . If a horizontal force = 30 N starts acting on the plank to the right ,the time after which the block will fall off the plank is (g = 10 ms^(-2))
View SolutionA block of mass m is placed in equilibrium on a moving plank. The maximum horizontal acceleration of the plank for mu=0.2 is:
View SolutionA block of mass m=2kg is placed in equilibrium on a moving plank accelerating with a=4m/s2 . If coefficient of friction between plank and block μ=0.2 . The friction force acting on theblock is:
View SolutionA block of mass m=2kg of shown dimensions is placed on a plank of mass M = 6Kg which is placed on smooth horizontal plane. The coefficient of friction between the block and the plank is mu=1/3 . If a horizontal froce F is applied on the plank, then find the maximum value of F (in N) for which the block and the plank move together
View SolutionA block of mass 2 kg rests on a rough horizontal plank , the coefficient of friction between the plank and block is 0.3. If the plank is pulled horizontally with a constant acceleration of 4m/s2 , the distance moved by the block on the plank in 5 second starting from rest (in m) is : (Take g = 10m/s2)
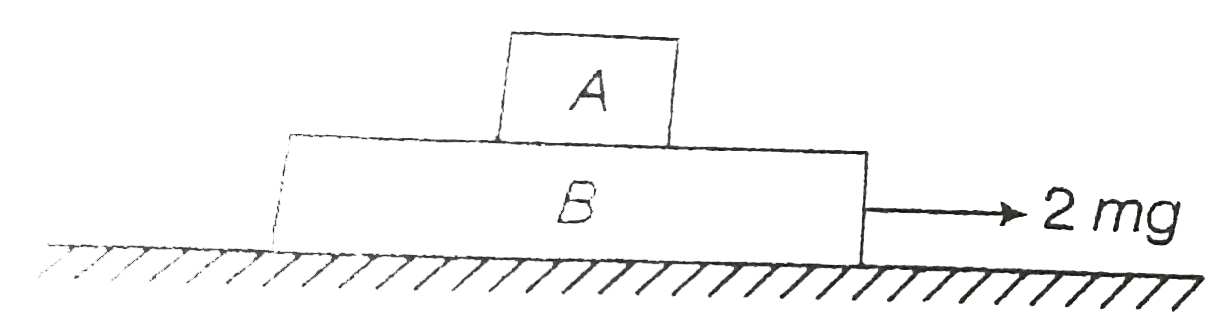
View SolutionBlock of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizontal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B, the acceleration of A relative to the plank and relative to the ground respectively, are
View SolutionA plank of mass 10 kg and a block of mass 2 kg are placed on a horizontal plane as shown in the figure. There is no friction between plane and plank. The coefficient of friction between block and plank is 0.5 .A force of 60 N is applied on plank horizontally. In first 2 s the work done by friction on the block is
View SolutionOn the horizontal surface of plank a block of mass 1 kg is placed (μ=0.6) which is stationary w.r.t. plank. Plank is moving with acceleration 5m/s2, then the frictional force on the block will be
View SolutionBlock A of mass m rests on the plank B of mass 3m which is free to slide on a frictionless horizontal surface. The coefficient of friction between the block and plank is 0.2. If a horizontal force of magnitude 2 mg is applied to the plank B. The acceleration of A relative to the plank is ng/5 where n is.

View Solution
