The potential energy function of a particle in the x-y plane is given by U=k(x+y), where (k) is a constant. The work done by the conservative force in moving a particlae from (1,1) to (2,3) is .
−3k
+3k
k
None of these
The correct Answer is:A
To find the work done by the conservative force in moving a particle from point (1,1) to point (2,3) given the potential energy function U=k(x+y), we can follow these steps:
Step 1: Identify the potential energy function
The potential energy function is given as:
U=k(x+y)
where k is a constant.
Step 2: Determine the initial and final positions
The initial position is (x1,y1)=(1,1) and the final position is (x2,y2)=(2,3).
Step 3: Calculate the initial potential energy
Substituting the initial coordinates into the potential energy function:
Uinitial=U(1,1)=k(1+1)=k⋅2=2k
Step 4: Calculate the final potential energy
Substituting the final coordinates into the potential energy function:
Ufinal=U(2,3)=k(2+3)=k⋅5=5k
Step 5: Calculate the change in potential energy
The change in potential energy ΔU is given by:
ΔU=Ufinal−Uinitial=5k−2k=3k
Step 6: Calculate the work done by the conservative force
The work done by the conservative force Wc is equal to the negative change in potential energy:
Wc=−ΔU=−3k
Final Answer
Thus, the work done by the conservative force in moving the particle from (1,1) to (2,3) is:
Wc=−3k
---
The potential energy function is given as:
U=k(x+y)
where k is a constant.
The initial position is (x1,y1)=(1,1) and the final position is (x2,y2)=(2,3).
Substituting the initial coordinates into the potential energy function:
Uinitial=U(1,1)=k(1+1)=k⋅2=2k
Substituting the final coordinates into the potential energy function:
Ufinal=U(2,3)=k(2+3)=k⋅5=5k
The change in potential energy ΔU is given by:
ΔU=Ufinal−Uinitial=5k−2k=3k
The work done by the conservative force Wc is equal to the negative change in potential energy:
Wc=−ΔU=−3k
Thus, the work done by the conservative force in moving the particle from (1,1) to (2,3) is:
Wc=−3k
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct9videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective15videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective27videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A particle is moving along the x-axis and force acting on it is given by F=F0sinωxN, where ω is a constant. The work done by the force from x=0 to x=2 will be
View SolutionThe potential energy function of a particle is given by U(r)=A2r2−B3r, where A and B are constant and r is the radial distance from the centre of the force. Choose the correct option (s)
View Solution
Knowledge Check
- Question 1 - Select One
The potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
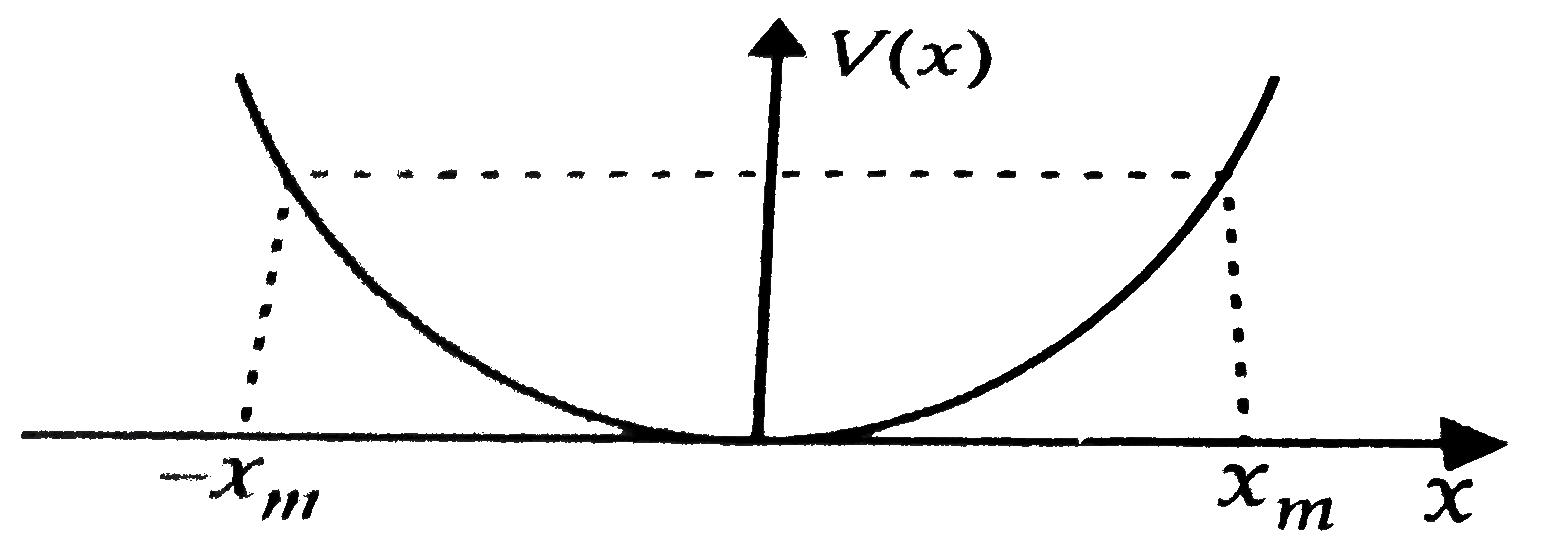 AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
The potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionThe potential energy of a particle of mass 5 kg moving in the x−y plane is given by U=(−7x+24y)J, where x and y are given in metre. If the particle starts from rest, from the origin, then the speed of the particle at t=2s is
View SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionThe potential energy U in joule of a particle of mass 1kg moving in x−y plane obeys the lawU=3x+4y, where (x,y) are the co-ordinates of the particle in metre. If the particle is at rest at (6,4) at time t=0 then :
View SolutionA particle is moving in a conservative force field from point A to point B.UA and UB are the potential energies of the particle at point A and B and WC is the work done by conservative forces in the process of taking the particle from A and B, which of the following is true?
View SolutionThe potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
View SolutionThe potential energy function for a particle executing simple harmonic motion is given by V(x)=12kx2, where k is the force constant of the oscillatore. For k=12Nm−1, show that a particle of total energy 1 joule moving under this potential must turn back when it reaches x=±2m.
View Solution

