Equal net forces act on two different block (A) and (B) masses (m) and 4(m) respectively For same displacement, identify the correct statement.
Their kinetic energies are in the ratio KAKB=14
Their speeds are in the ration vAvB=11
Work done on the block are in the ratio WAWB=11
All of the above
The correct Answer is:C
To solve the problem, we need to analyze the situation where equal net forces act on two blocks (A and B) with masses m and 4m respectively, for the same displacement. We will derive the relationships between work done, kinetic energy, and speed for both blocks.
Step 1: Understand the Work Done
The work done (W) on an object is given by the formula:
W=F⋅S
where F is the force applied and S is the displacement. Since equal net forces act on both blocks and the displacement is the same, we can denote the force as F and the displacement as S.
Step 2: Calculate Work Done on Both Blocks
For both blocks A and B:
- Work done on block A, WA=F⋅S
- Work done on block B, WB=F⋅S
Since both forces and displacements are equal:
WA=WB
Thus, the ratio of work done on block A to block B is:
WAWB=1:1
Step 3: Apply the Work-Energy Theorem
According to the work-energy theorem, the work done on an object is equal to the change in its kinetic energy. Therefore, we can write:
WA=KEAandWB=KEB
Since WA=WB, we have:
KEA=KEB
This implies:
KEAKEB=1:1
Step 4: Relate Kinetic Energy to Speed
The kinetic energy (KE) of an object is given by:
KE=12mv2
For block A:
KEA=12mv2A
For block B:
KEB=12(4m)v2B=2mv2B
Setting the kinetic energies equal gives:
12mv2A=2mv2B
Dividing both sides by m (assuming m≠0):
12v2A=2v2B
Rearranging gives:
v2A=4v2B
Taking the square root:
vAvB=2:1
Conclusion
From our analysis:
- The work done on both blocks is in the ratio 1:1.
- The kinetic energy of both blocks is also in the ratio 1:1.
- The speeds of the blocks are in the ratio 2:1.
Thus, the correct statement is that the work done on the blocks is in the ratio 1:1.
Final Answer
The correct statement is that the work done on blocks A and B is in the ratio 1:1.
The work done (W) on an object is given by the formula:
W=F⋅S
where F is the force applied and S is the displacement. Since equal net forces act on both blocks and the displacement is the same, we can denote the force as F and the displacement as S.
For both blocks A and B:
- Work done on block A, WA=F⋅S
- Work done on block B, WB=F⋅S
WA=WB
Thus, the ratio of work done on block A to block B is:
WAWB=1:1
According to the work-energy theorem, the work done on an object is equal to the change in its kinetic energy. Therefore, we can write:
WA=KEAandWB=KEB
Since WA=WB, we have:
KEA=KEB
This implies:
KEAKEB=1:1
The kinetic energy (KE) of an object is given by:
KE=12mv2
For block A:
KEA=12mv2A
For block B:
KEB=12(4m)v2B=2mv2B
Setting the kinetic energies equal gives:
12mv2A=2mv2B
Dividing both sides by m (assuming m≠0):
12v2A=2v2B
Rearranging gives:
v2A=4v2B
Taking the square root:
vAvB=2:1
From our analysis:
- The work done on both blocks is in the ratio 1:1.
- The kinetic energy of both blocks is also in the ratio 1:1.
- The speeds of the blocks are in the ratio 2:1.
The correct statement is that the work done on blocks A and B is in the ratio 1:1.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct9videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective15videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective27videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
Two blocks of mass M and m are kept on the trolley whose all surfaces are smooth select the correct statement
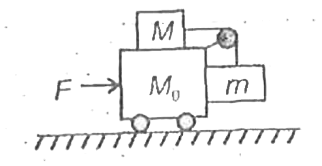 View Solution
View SolutionChoose the correct option:
A system of two blocks A and B and a wedge C are released from rest as shown in figure . Masses of the blocks and the wedge are m , 2m and 2m respectively . The displacement of wedge C when block B slides down the plane a distance 10 cm is ( neglect friction )
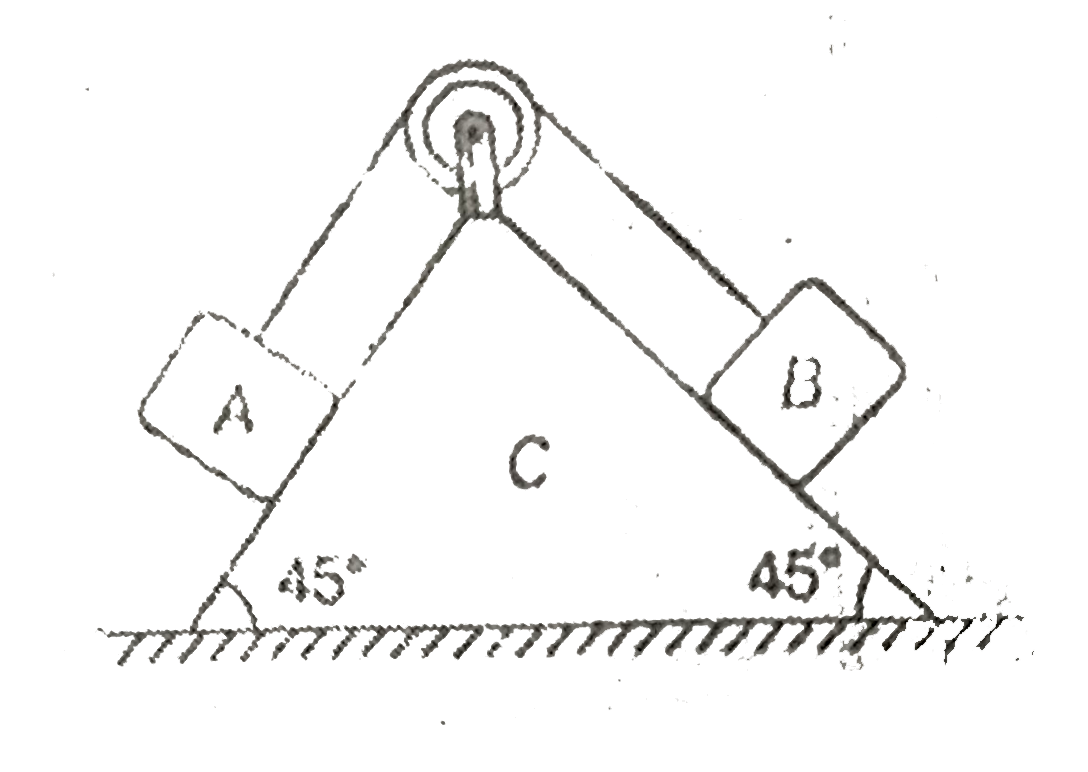 View Solution
View SolutionA constant force actson a body of mass m, at rest and produces a velocity 'v' over a displacement 's1'. The same force acts on another body of mass m2 at rest and produces the same velocity. 'v' over a displacement 's2'. The ratio of the displacements is
View SolutionA block pulley arrangement is shown in the figure. If f1andf2 represents frictional force acting on the block A and B respectively then choose the correct statement. (given g=10m/s2)
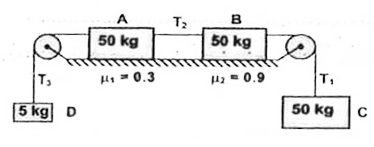 View Solution
View SolutionIn the figure the masses of the blocks A and B are same and each equal to m. The tensions in the strings OA and AB are T2 and T1 respectively. The system is in equilibrium with a constant horizontal force mg on B. The tension T1 is :-
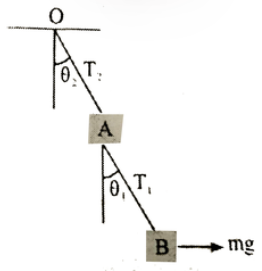 View Solution
View SolutionTwo blocks 'A' and 'B' having masses mA and ma, respectively are connectd by an arrangement shown in the figure. Calculate the downward acceleration of the block B. Assume the pulleys to be massless. Under what condition will block A have downward acceleration?
 View Solution
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
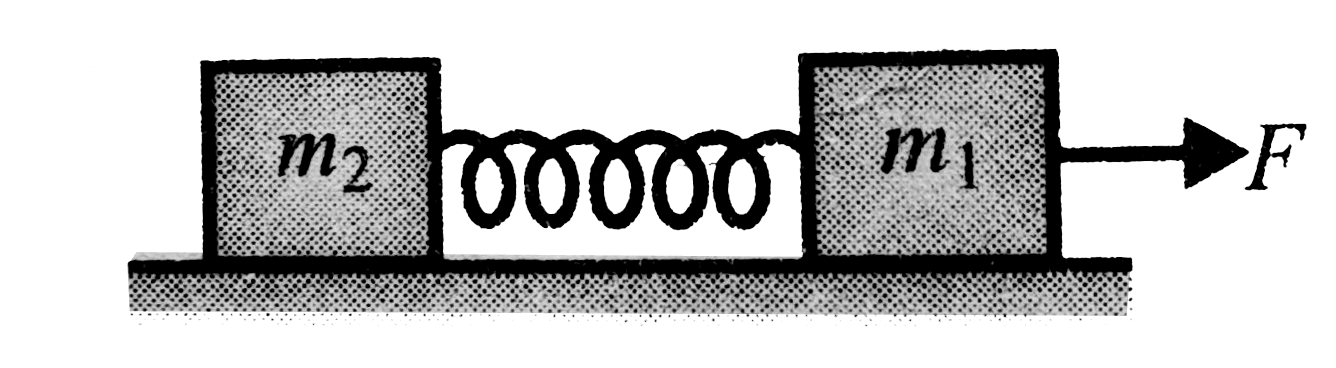
Which of the following statement is not true tn the watt of above system.View SolutionTwo blocks A and B of mass mAandmB respectively are kept in contact on a frictionless table. The experimenter pushes the block A from behind so that the blocks accelerate. If the block A exerts a fore F on the block B, what is the force exerted by the experimenter on A?
View SolutionTwo blocks A and B of mass 2 kg and 4 kg respectively are placed on a smooth inclined plane and 2 kg block is pushed by a force F acting parallel to the plane as shown. If N be the magnitude of contact force applied on B by A, which of the following is/are correct?
 View Solution
View SolutionTwo blocks A and B each of mass m are placed on a smooth horizontal surface. Two horizontal force F and 2F are applied on blocks A and B, respectively, as shown in fig. Block A does not slide on block B. Then then the normal reaction acting between the two blocks is (assume no friction between the blocks)
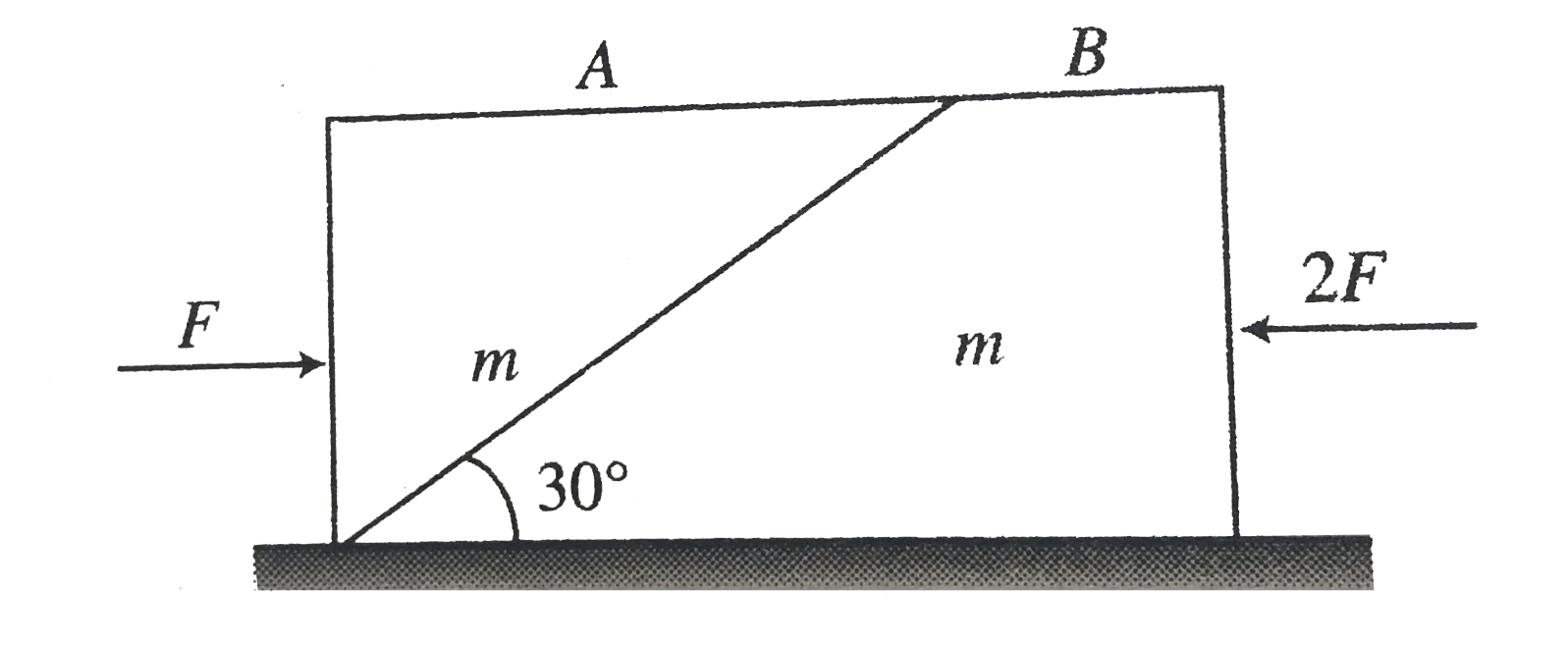 View Solution
View Solution

