A block tied between identical springs is in equilibrium. If upper spring is cut, then the acceleration of the block just after cut is 5ms1 Now if instead of upper string lower spring is cut, then the acceleration of the block just after the cut will be (Take g=10m/s2).
1.25ms−2
5ms−2
10ms−2
2.5ms−2
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the block when one of the springs is cut. Let's break it down step by step.
1. Understanding the Setup:
- We have a block of mass m suspended between two identical springs.
- The weight of the block mg acts downwards, where g=10m/s2.
- The forces exerted by the springs are F1 (upper spring) and F2 (lower spring).
2. Equilibrium Condition:
- In equilibrium, the forces acting on the block must balance out. Thus, we have:
F1+F2=mg(Equation 1)
3. Cutting the Upper Spring:
- When the upper spring F1 is cut, the only forces acting on the block are its weight mg downwards and the force F2 from the lower spring upwards.
- The net force acting on the block can be expressed as:
mg - F_2 = ma \quad \text{(where a = 5 \, \text{m/s}^2 )}
- Substituting g=10m/s2:
10m−F2=5m
- Rearranging gives:
F2=10m−5m=5m(Equation 2)
4. Finding F1:
- Now, substituting F2 back into Equation 1:
F1+5m=10m
- Thus, we find:
F1=10m−5m=5m(Equation 3)
5. Cutting the Lower Spring:
- Now, consider the scenario where the lower spring F2 is cut.
- The forces acting on the block are its weight mg downwards and the force F1 from the upper spring upwards.
- The net force can be expressed as:
mg - F_1 = ma' \quad \text{(where a' is the new acceleration)}
- Substituting g=10m/s2 and F1=5m:
10m−5m=ma′
- This simplifies to:
5m=ma′
- Dividing both sides by m (assuming m≠0):
a′=5m/s2
Final Answer:
The acceleration of the block just after cutting the lower spring is 5m/s2.
- We have a block of mass m suspended between two identical springs.
- The weight of the block mg acts downwards, where g=10m/s2.
- The forces exerted by the springs are F1 (upper spring) and F2 (lower spring).
- In equilibrium, the forces acting on the block must balance out. Thus, we have:
F1+F2=mg(Equation 1)
- When the upper spring F1 is cut, the only forces acting on the block are its weight mg downwards and the force F2 from the lower spring upwards.
- The net force acting on the block can be expressed as:
mg - F_2 = ma \quad \text{(where a = 5 \, \text{m/s}^2 )}
- Substituting g=10m/s2:
10m−F2=5m
- Rearranging gives:
F2=10m−5m=5m(Equation 2)
- Now, substituting F2 back into Equation 1:
F1+5m=10m
- Thus, we find:
F1=10m−5m=5m(Equation 3)
- Now, consider the scenario where the lower spring F2 is cut.
- The forces acting on the block are its weight mg downwards and the force F1 from the upper spring upwards.
- The net force can be expressed as:
mg - F_1 = ma' \quad \text{(where a' is the new acceleration)}
- Substituting g=10m/s2 and F1=5m:
10m−5m=ma′
- This simplifies to:
5m=ma′
- Dividing both sides by m (assuming m≠0):
a′=5m/s2
The acceleration of the block just after cutting the lower spring is 5m/s2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct9videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective15videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective27videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A block tied between two identical springs is in equilibrium. If upper spring is cut then the acceleration of the block just after cut is 6m/s2 downwards. Now, if instead of upper spring, lower spring is being cut then the acceleration of the block just after the cut will be.
 View Solution
View SolutionIf the lower spring is cut, find acceleration of the blokcs, immediately after cutting the spring.
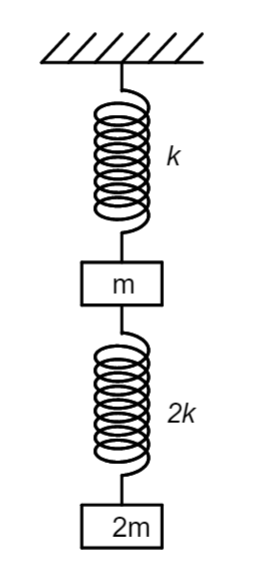 View Solution
View SolutionA block is attached with an ideal spring and string, and is in equilibrkum as shown in Figure. The acceleration of the block just after breaking the string is a1 and just after breaking the spring is a2. Then
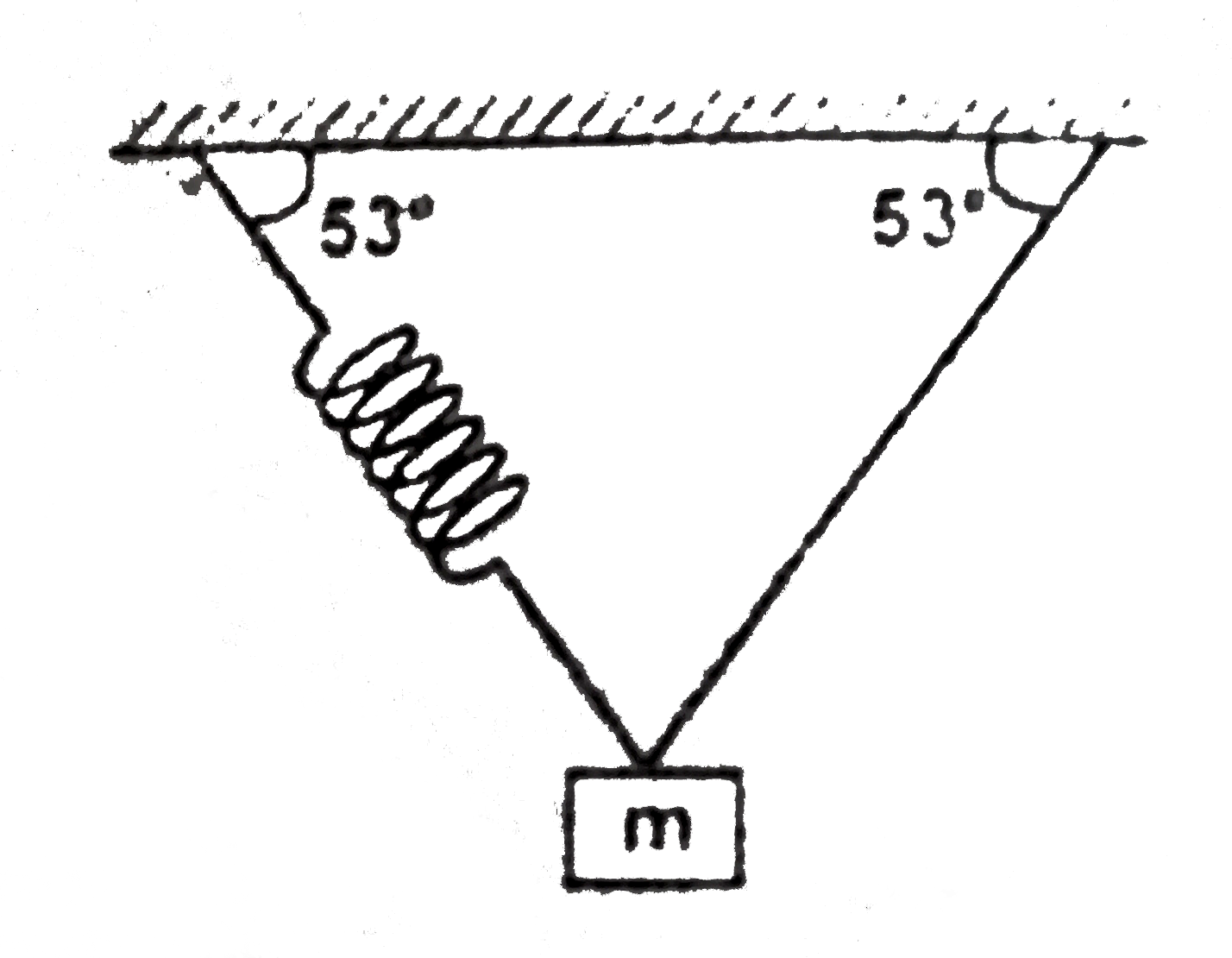 View Solution
View SolutionFind the acceleration of block A immediately after the string is cut .
 View Solution
View SolutionThe system shown in the figure is in equilibrium at rest. The spring and string are massless Now the string is cut. Find the acceleration of the blocks just after the string is cut.
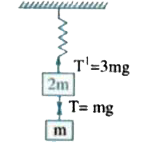 View Solution
View SolutionTwo block of mass 2kg are connected by a massless ideal spring of spring contant K=10N/m . The upper block is suspended from roof by a light string A . The system shown is in equilibrium. The string A is now cut, the acceleration of upper block just after the string A is cut will be (g=10m/s2 .
 View Solution
View SolutionTwo block of mass 2kg are connected by a massless ideal spring of spring contant K=10N/m . The upper block is suspended from roof by a light string A . The system shown is in equilibrium. The string A is now cut, the acceleration of upper block just after the string A is cut will be (g=10m/s2 .
 View Solution
View SolutionThe system shown in figure is initially in equilibrium. What is the acceleration of B just after the string connecting B to ground is cut ?
 View Solution
View SolutionIn figure shown if 2 kg block is moving at an acceleration 2m/s2, find the elongationin spring and acceleration of 4 kg block at this instant. Take g= 10m/s2.
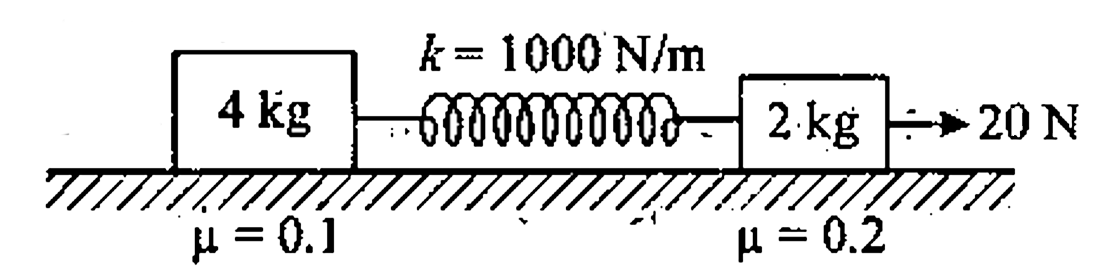
View SolutionSystem shown in fig is in equilibrium and at rest. The spring and string are massless now the string is cut. The acceleration of mass 2m and m just after the string is cut will be:
 View Solution
View Solution

