One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacment, the work done by the spring is +(12)kx2. The possible cases are.
The spring was initially compessed by a distance x and was finally in its natural length .
It was initially stretched by a distance x and finally was in its natural length.
It was initially natural length and finally in a compressed position.
It was initially in its natural length and finally in a stretched position.
The correct Answer is:A, B
To solve the problem, we need to analyze the work done by a spring in different scenarios involving its compression and elongation. The work done by the spring is given by the formula:
W=12kx2
where W is the work done, k is the spring constant, and x is the displacement from the spring's natural length.
1. Understand the Spring's Behavior:
The spring can either be compressed or stretched. The work done by the spring depends on the initial and final positions of the spring.
2. Analyze Each Case:
- Case 1: The spring is initially compressed by a distance x and then returns to its natural length.
- Here, the spring does positive work as it moves from a compressed state to its natural length.
- Work done: W=12kx2 (positive).
- Case 2: The spring is initially stretched by a distance x and then returns to its natural length.
- Similar to Case 1, the spring does positive work as it moves from a stretched state to its natural length.
- Work done: W=12kx2 (positive).
- Case 3: The spring is initially at its natural length and then is compressed.
- In this case, the spring is being compressed, and it stores potential energy. However, the work done by the spring is not applicable here since it is not returning to a natural position.
- Work done: W=0 (no displacement from natural length).
- Case 4: The spring is initially at its natural length and then is stretched.
- Similar to Case 3, the spring is being stretched, and it stores potential energy but does not perform work on the block as it is not returning to a natural position.
- Work done: W=0 (no displacement from natural length).
3. Conclusion:
The only cases where the spring does work on the block are Case 1 and Case 2. Therefore, the possible cases where work is done by the spring are:
- Case 1: Initially compressed to natural length.
- Case 2: Initially stretched to natural length.
Final Answer:
The correct options are Case 1 and Case 2.
---
The spring can either be compressed or stretched. The work done by the spring depends on the initial and final positions of the spring.
- Case 1: The spring is initially compressed by a distance x and then returns to its natural length.
- Here, the spring does positive work as it moves from a compressed state to its natural length.
- Work done: W=12kx2 (positive).
- Case 2: The spring is initially stretched by a distance x and then returns to its natural length.
- Similar to Case 1, the spring does positive work as it moves from a stretched state to its natural length.
- Work done: W=12kx2 (positive).
- Case 3: The spring is initially at its natural length and then is compressed.
- In this case, the spring is being compressed, and it stores potential energy. However, the work done by the spring is not applicable here since it is not returning to a natural position.
- Work done: W=0 (no displacement from natural length).
- Case 4: The spring is initially at its natural length and then is stretched.
- Similar to Case 3, the spring is being stretched, and it stores potential energy but does not perform work on the block as it is not returning to a natural position.
- Work done: W=0 (no displacement from natural length).
The only cases where the spring does work on the block are Case 1 and Case 2. Therefore, the possible cases where work is done by the spring are:
- Case 1: Initially compressed to natural length.
- Case 2: Initially stretched to natural length.
The correct options are Case 1 and Case 2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective15videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective30videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is
 View Solution
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is
 View Solution
View SolutionOne end of a spring of force constant K is fixed to a vertical wall and other to a body of mass m resting on smooth horizontal surface. There is another wall at a distance of √3x0 from the body. If all the collisions are elastic and spring is compressed by 2x0and released, then the time period of oscillation is
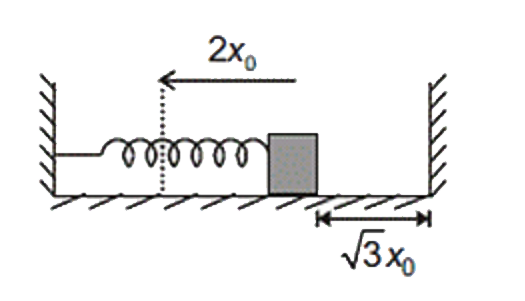 View Solution
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionOne end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in fig. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
[ sin 37∘ = 3/5]
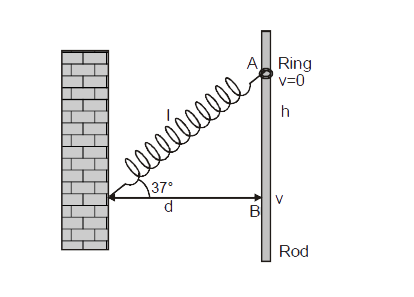 View Solution
View SolutionOn end of a light spring of natural length d and spring constant k is fixed on a rigid wall and the other is attached to a smooth ring of mass m which can slide without friction on a vertical rod fixed at a distance d from the wall. Initially the spring makes an angle of 37∘ with the horizontal. as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal. (sin37∘=35).
 View Solution
View SolutionOne end of a light spring of natural length 4m and spring constant 170 N/m is fixed on a rigid wall and the other is fixed to a smooth ring of mass 12 kg which can slide without friction in a verical rod fixed at a distance 4 m from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
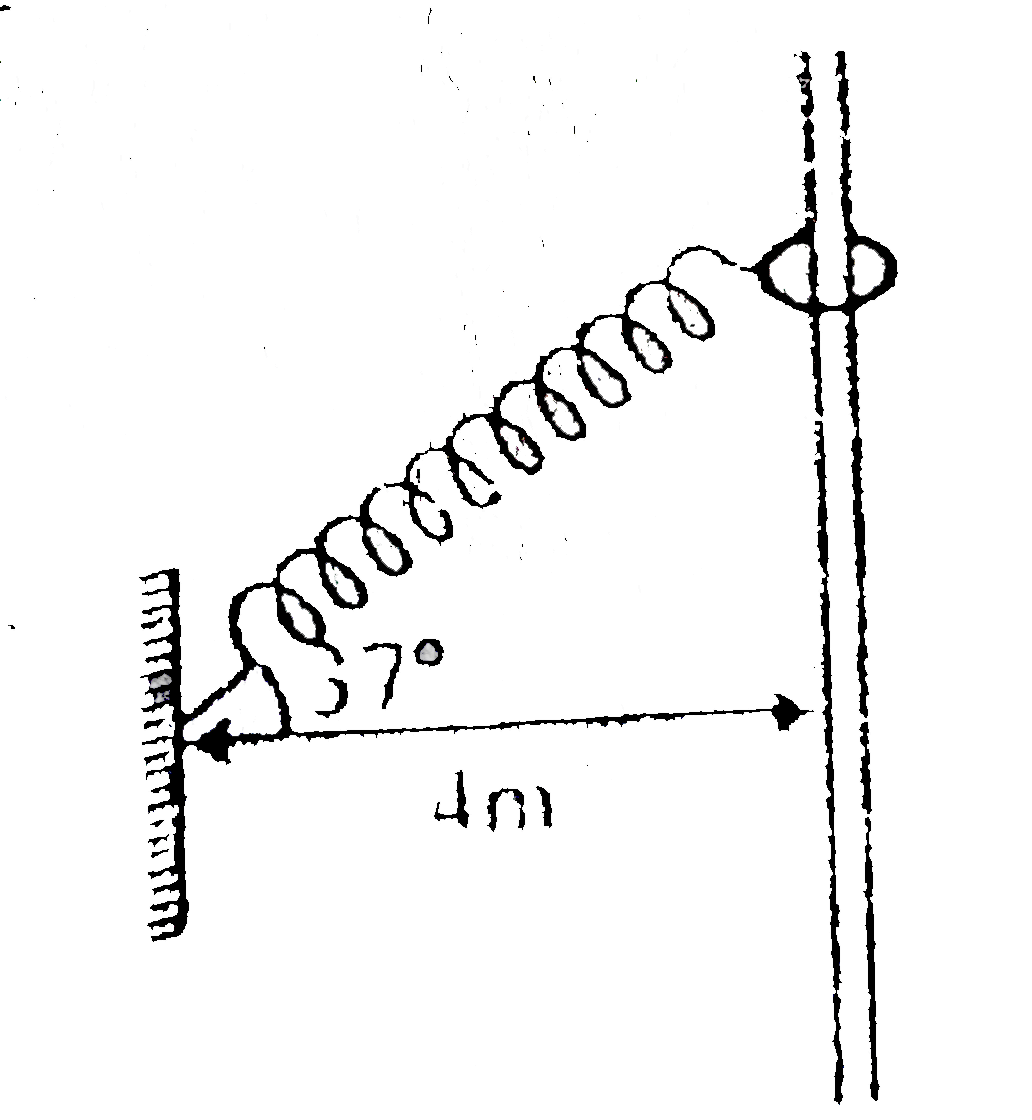 View Solution
View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .View Solution
.View SolutionTwo blocks, of masses M and 2M, are connected to a light spring of spring constant K that has one end fixed, as shown in figure. The horizontal surface and the pulley are frictionless. The blocks are released from when the spring is non deformed. The string is light.
 .View Solution
.View Solution

