At two positons kinetic energy and potential energy of a particle are K1=10J:U1=−20J,K2=20J,U2=−10J. In moving from 1 to 2 .
work done by conservative forces is positive.
work done by conservative forces is negative.
work done by all the forces is positive .
work done by all the forces is negative.
The correct Answer is:B, C
To solve the problem, we need to analyze the kinetic and potential energies at two positions and determine the work done by conservative forces and by all forces as the particle moves from position 1 to position 2.
Step 1: Identify the given values
We have the following values:
- Kinetic energy at position 1, K1=10J
- Potential energy at position 1, U1=−20J
- Kinetic energy at position 2, K2=20J
- Potential energy at position 2, U2=−10J
Step 2: Calculate the work done by conservative forces
The work done by conservative forces can be calculated using the change in potential energy:
Wconservative=U1−U2
Substituting the values:
Wconservative=(−20)−(−10)=−20+10=−10J
This indicates that the work done by conservative forces is negative.
Step 3: Calculate the work done by all forces
The work done by all forces can be calculated using the change in kinetic energy:
Wall=K2−K1
Substituting the values:
Wall=20−10=10J
This indicates that the work done by all forces is positive.
Step 4: Summarize the results
From the calculations:
- Work done by conservative forces: Wconservative=−10J (negative)
- Work done by all forces: Wall=10J (positive)
Conclusion
Based on the results:
- The work done by conservative forces is negative.
- The work done by all forces is positive.
Thus, the correct options are:
- Work done by conservative forces is negative.
- Work done by all forces is positive.
We have the following values:
- Kinetic energy at position 1, K1=10J
- Potential energy at position 1, U1=−20J
- Kinetic energy at position 2, K2=20J
- Potential energy at position 2, U2=−10J
The work done by conservative forces can be calculated using the change in potential energy:
Wconservative=U1−U2
Substituting the values:
Wconservative=(−20)−(−10)=−20+10=−10J
This indicates that the work done by conservative forces is negative.
The work done by all forces can be calculated using the change in kinetic energy:
Wall=K2−K1
Substituting the values:
Wall=20−10=10J
This indicates that the work done by all forces is positive.
From the calculations:
- Work done by conservative forces: Wconservative=−10J (negative)
- Work done by all forces: Wall=10J (positive)
Based on the results:
- The work done by conservative forces is negative.
- The work done by all forces is positive.
- Work done by conservative forces is negative.
- Work done by all forces is positive.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective15videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective30videos
WORK, ENERGY & POWER
- BOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A body is displaced from position A to position B. Kinetic and potential energies of the body at positions A and B are
KA=50J,UA=−30J,KB=−10J and UB=20J.
Find work done by
(a) conservative forces (b) all forces (c)forces other than covservative forces.View SolutionThe potential energy of 1 kg particle is [U(x)=(0.25x4)−(0.5x2)] J If total mechanical energy is 2 J, then maximum KE is
View SolutionIn position A kinetic energy of a particle is 60 J and potential energy is -20 J. In position B, kinetic energy is 100 J and potential energy is 40 J. Then, in moving the particle from A to B
View SolutionAt what displacement the kinetic is equal to the potential energy ?
Hint :U=12kx2,K=12(A2−x2)
U=KView SolutionThe potential energy of a particle under a conservative force is given by U(x)=(x2−3x) J. The equilibrium position of the particle is at
View SolutionA partical of mass 2kg is moving on the x−axis with a constant mechanical energy 20J. Its potential energy at any x is U=(16−x2)J where x is in metre. The minimum velocity of particle is :−
View SolutionIn the diagram, the graph between volume and pressure for a thermodynamical process in shown. If UA=0,UB=20J and the energy given from B to C is 30J, then at the stage of C, the internal energy of the system is –
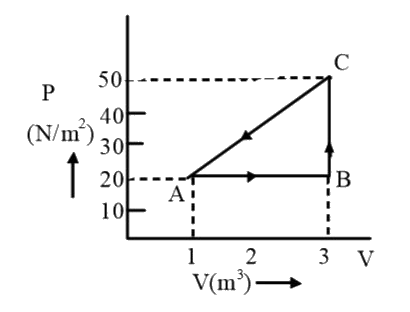 View Solution
View SolutionThe kinetic energy of two moles of N2at27∘Cis(R=8.314JK−1mol−1)
View SolutionA particle of mass 0.5 kg is subjected to a force which varies with distance as shown in figure

1. The work done by the force during the displacement from x=0 to x=4andx=4 to x=12are respectively
(1)20J,40J(2)40J,40J(3)20J,60J(4)40J,80J
2. The increaase in kinetic energy of the particle during its displac ement from x=0 to x=12 m is
(1)20J(2)40J(3)80J(4)120J
3. If the speed of the particle at x=0 is 4 m/s, its speed st x=8 m is
(1)8m/s(2)16m/s(3)32m/s(4)4m/sView SolutionWhen a thermodynamic system is taken from an initial state I to a final state F along the path IAF, as shown in Fig. the heat energy absorbed by the system is Q=55J and work done by the system is W=25J. If the same system is taken along the path IBF, the value of Q=35J.
(a) If W=−15J for the curved path FI, how much heat energy is lost by the system along this path ?
(b) If U1=10J, what is UF ?
(d) If UB=20J, what is Q for the process BF and IB ?View Solution

