In the figure shown masses of the blocks A, B and C are 6kg, 2kg and 1kg respectively. Mass of the spring is negligibly small and its stiffness is 1000 N//m. The coefficient of friction between the block A and the table is μ=0.8. Initially block C is held such that spring is in relaxed position. The block is released from rest. Find (g=10m/s2).

The correct Answer is:A, B, C
μmAg=0.8×6×10=48N
(mB+mC)g=(1+2)×10=30N
Since (mB−mC)g>μmAg,aA=aB=0.
From conservation of energy principal we can prove that maximum distance moved by C or maximum extension in the spring would be
xm=2mCgk=2×1×101000
=0.02m
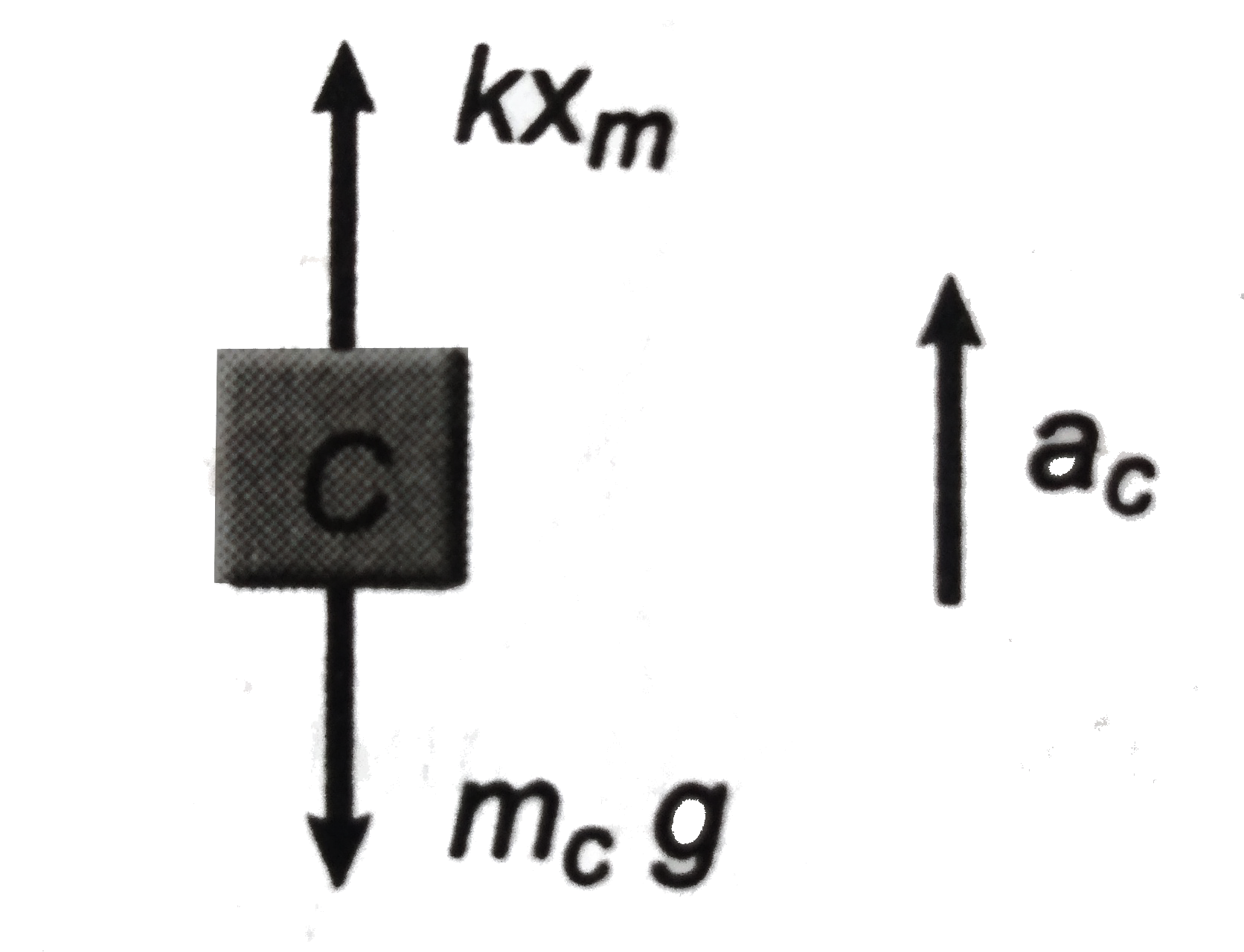
At maximum extension
aC=kxm−mCgmC
Substituting the values we have,
aC=10m/s2.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct
9 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Three blocks A, B and C, whose masses are 9kg, 9kg and 18kg respectively as shown in the figure, are released from rest. The co-efficient of friction between block A and the horizontal surface is 0.5 & the co-efficient of friction between block B and the horizontal surface is 0.5. Find the acceleration of block C just release [Take g=10m/s2]. All strings and pulleys are ideal
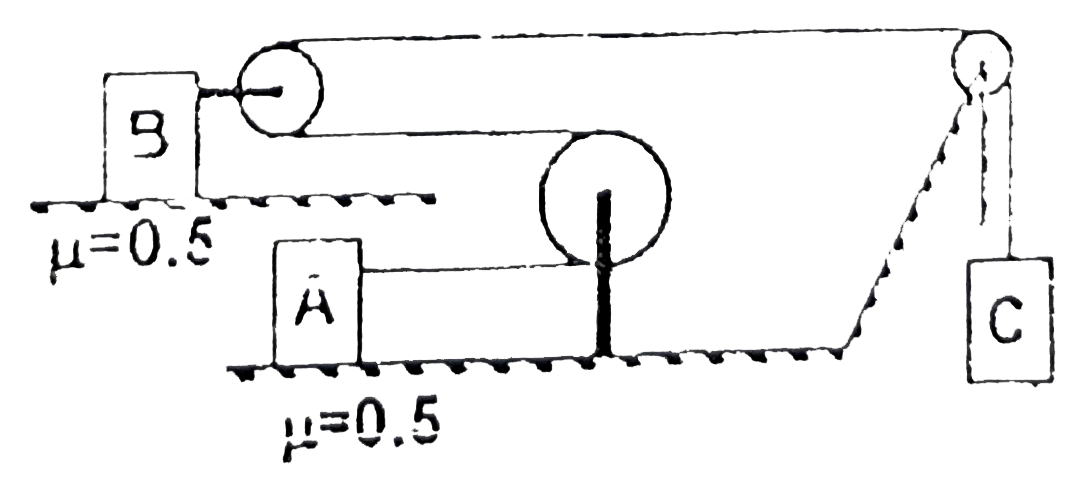
View SolutionTwo blocks of masses m1=10kg and m2=20kg are connected by a spring of stiffness k = 200 N/m. The coefficient of friction between the blocks and the fixed horizontal surface is μ=0.1. Find the minimum constant horizontal force F (in Newton) to be applied to m1 in order to slide the mass m2. (Take g=10m/s2)
View Solution
Knowledge Check
A block of mass m=2kg is resting on a rough inclined plane of inclination of 30∘ as shown in figure. The coefficient of friction between the block and the plane is μ=0.5. What minimum force F should be applied perpendicular to the plane on the block, so that blocks does not slip on the plane? (g=10m/s2)
 A2.68 NBZeroC4.34 ND6.24 N
A2.68 NBZeroC4.34 ND6.24 N
Consider the system shown in the figure. Coefficient of friction between the block and table is μ=0.5. The system is released from rest. Find the work done by friction, when the speed of block is 10 m/s (m=1kg)

View SolutionA block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
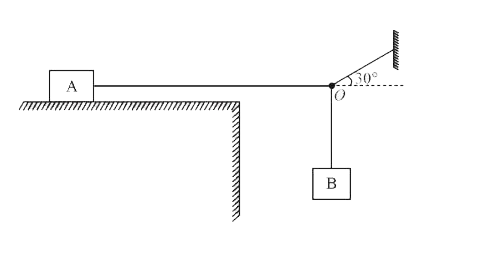
View SolutionThe block A in the given figure is of mass 10√3 kg The coefficient of friction between the block and the surface on which it rests is 0.5. Find maximum mass of block B possible such that the system will be in equilibrium is.
View SolutionA force of 200N is applied as shown in the figure on block of 3 kg. The coefficient of friction between the block and the wall is 0.3. Find the friction acting on the block. (in N) {Take g = 10 m/s2

View SolutionIn the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.

View SolutionA block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionDetermine the acceleration of the 5kg block A . Neglect the mass of the pulley and cords . The block B has a mass of 10kg, The coefficient of kinetic friction between block B and the surface is μk=0.1 (take g=10m/s2)

View Solution
