A 10kg ball attached at the end of a rigid massless rod of lengh 1m rotates at constant speed in a horizontal circle of radius 0.5m and period of 1.58s , as shown in the figure. The force exerted by the rod on the ball is (g=10ms−2)

158N
128N
110N
98N
The correct Answer is:B
v=22πrT=(2π)(0.5)1.58
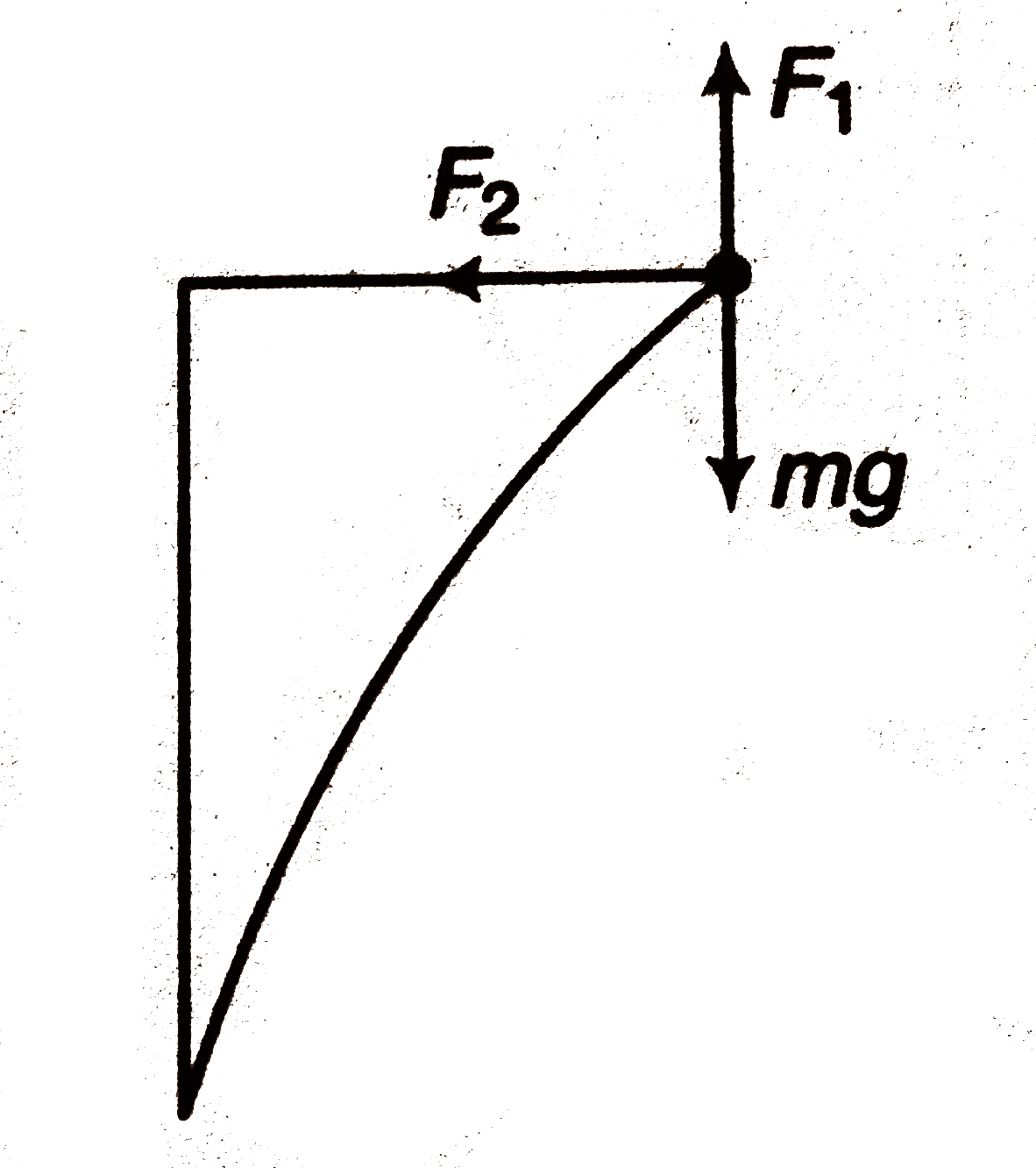
≈2m/s
F1=mg=100N
F2=mv2r=10×40.5=80N
:. Net force +by rod on ball
=√F21+F22=128N
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A particle is attached to an end of a rigid rod. The other end of the rod is hunged and the rod rotates always remaining horizontal. Its angular speed is increasing at contant rate. The mass of the particle is m . The force exerted by the rod on the particle is →F , then:
View SolutionA ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is

View SolutionA body of mass 1 kg is rotated in a horizontal circle of radius 1 m and moves with velocity 2ms−1 The work done in 10 revolutions is
View SolutionA ball of mass 0.6kg attached to a light inextensible string rotates in a vertical circle of radius 0.75m such that it has speed of 5ms−1 when the string is horizontal. Tension in the string when it is horizontal on other side is (g=10ms−2).
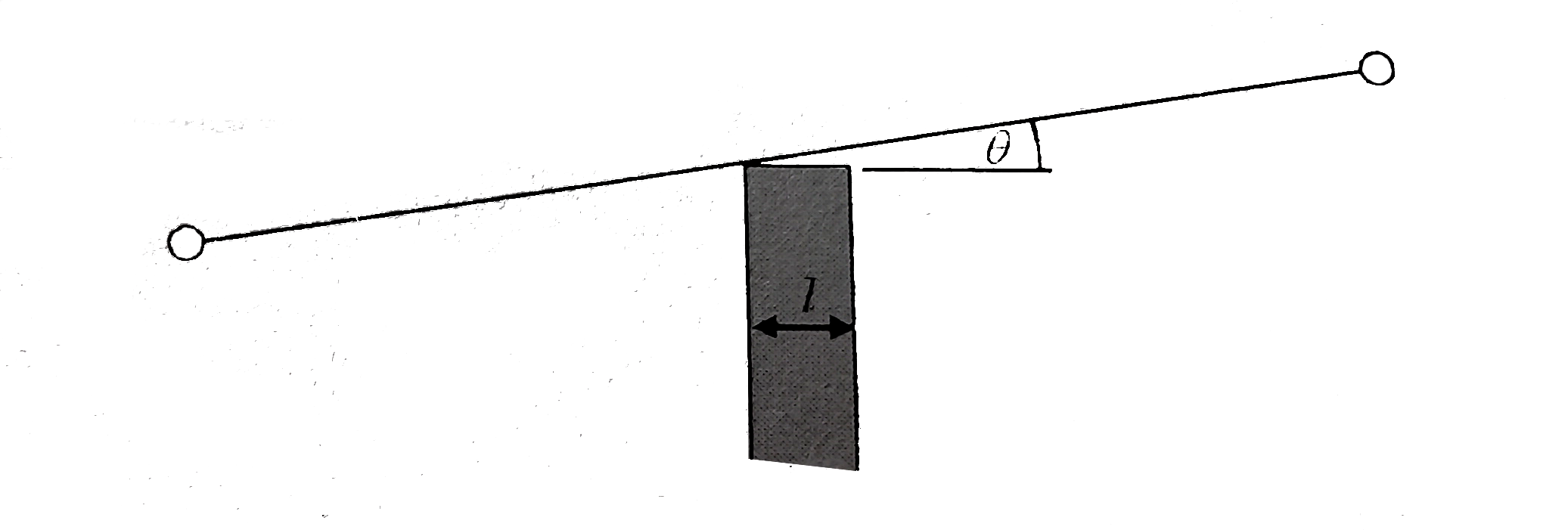
View SolutionTwo identical small balls each of mass m are rigidly affixed at the ends of light rigid rod of length 1.5m and the assmebly is placed symmetrically on an elevated protrusion of width l as shown in the figure.
The rod-ball assmebly is titled by a small angle theta in the vertical plane as shown in the figure and released. Estimate time-period (in seconds) of the oscillation of the rod-ball assembly assuming collisions of the rod with corners of the protrusion to be perfectly elastic and the rod does not slide on the corners. Assume θ=gl (numerically in radians), where g is the acceleration of free fall.
View SolutionA ball of mass 1 kg is released from position A inside a wedge with a hemispherical cut of radius 0.5 m as shown in figure. The force exerted by the wedge on ball, when the ball is in position B is (neglect friction everywhere) (Take g=10m/s2)

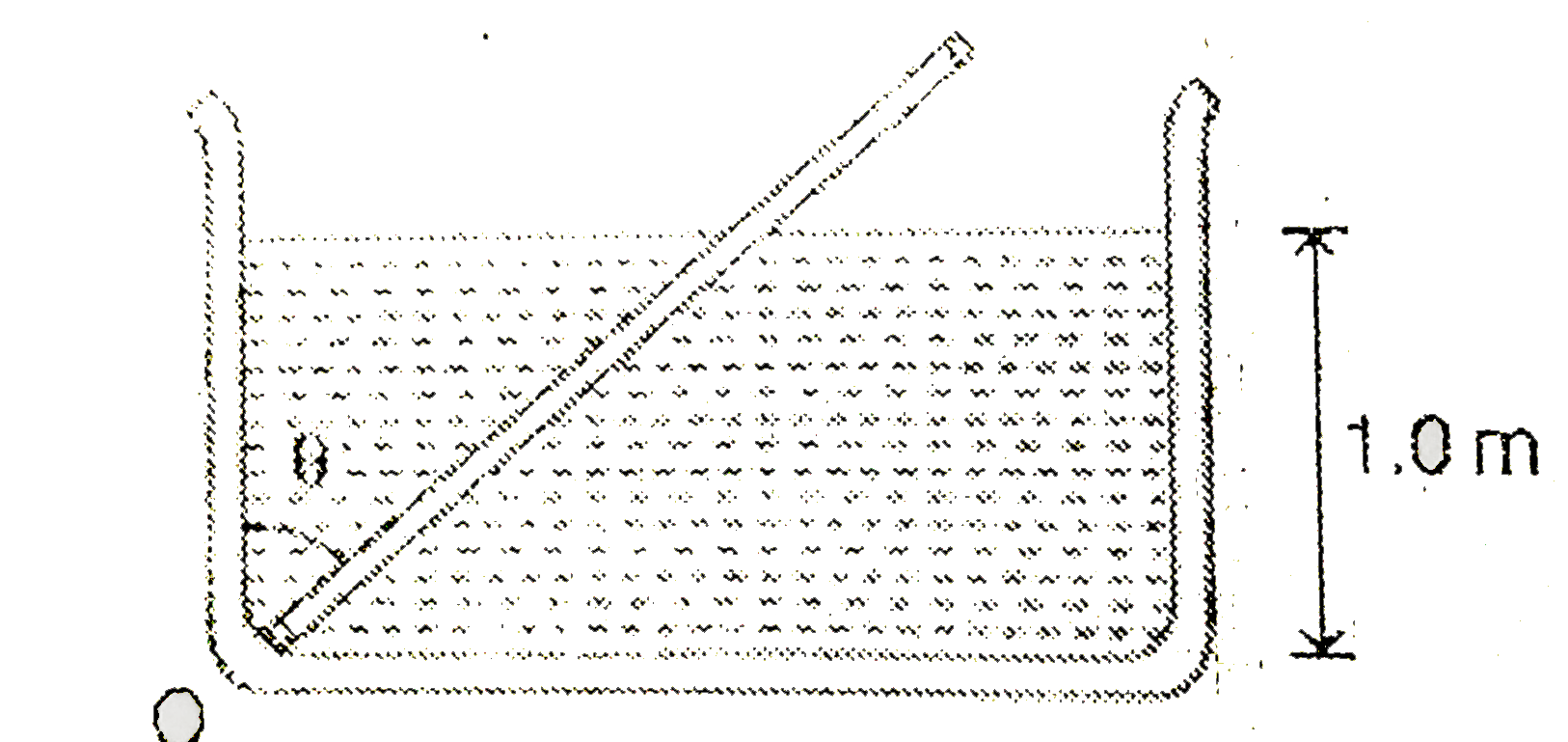
View SolutionA uniform rod of length 2.0 m specific gravity 0.5 and mass 2 kg is hinged at one end to the bottom of a tank of water (specific gravity = 10) filled upto a height o f 1.0 m as shown in figure. Taking the case θ=−0∘ the force exerted by the hings on the rod is (g=10m/s2)
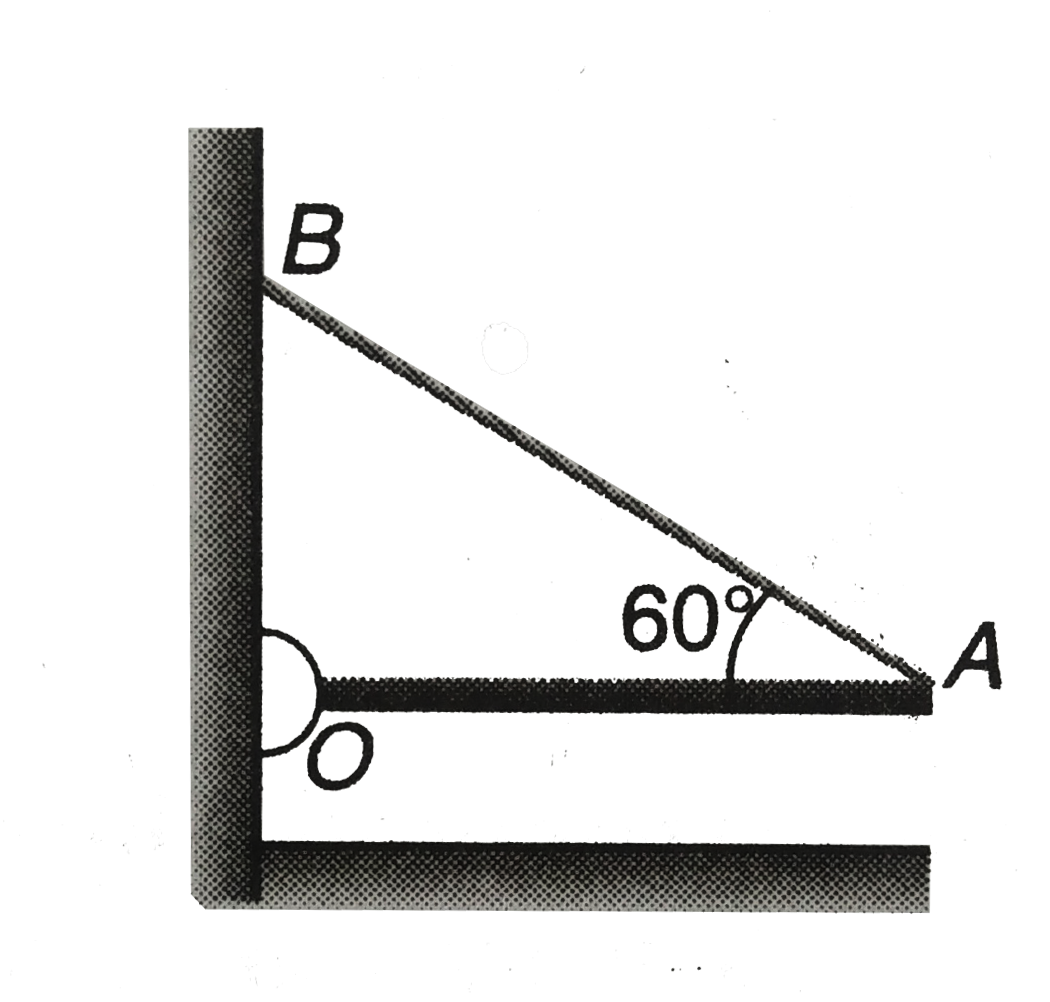
View SolutionA rod OA of mass 4kg is held in horizontal position by a massless string AB as shown in figure. Length of the rod is 2m. Find
(a) tension in the string
(b) net force exerted by hings on the rod. (g=10m/s2)
View SolutionA 1kg stone at the end of 1m long string is whirled in a vertical circle at a constant speed of 4m/s. The tension in the string is 6N, when the stone is at (g=10m/s2)
View SolutionA uniform rod of length 50 cm is released in the vertical plane from the position shown in the figure. The rod is hinged smoothly at O. The angular speed of rod when it becomes horizontal is ( take g=10ms−2 )
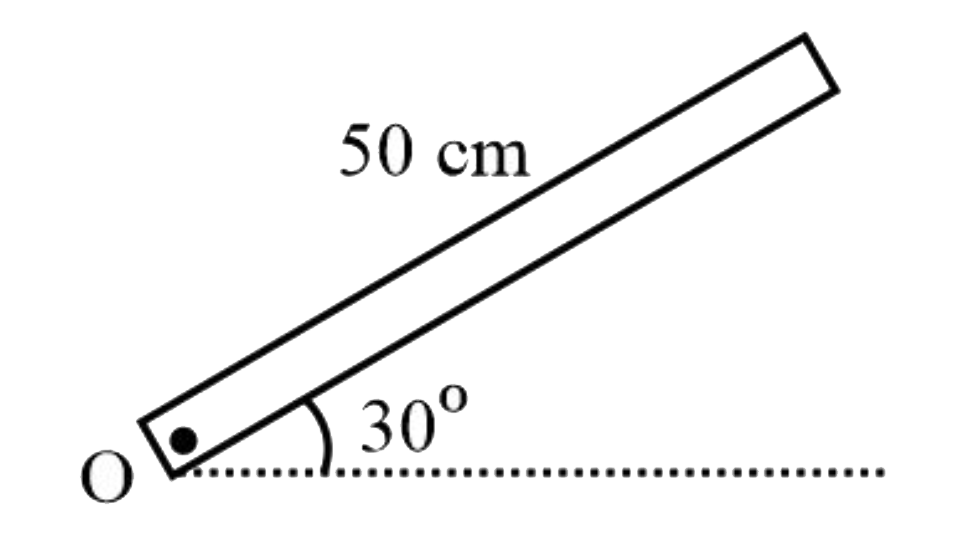
View Solution
