After a completely inelastic collision two objects of the same mass and same initial speed are found to move away together at half their initial speed. Find the angle between the initial velocities of the objects.
The correct Answer is:A, B
Let θ be the desired angle. Linear momentum of the system will remain conserved.
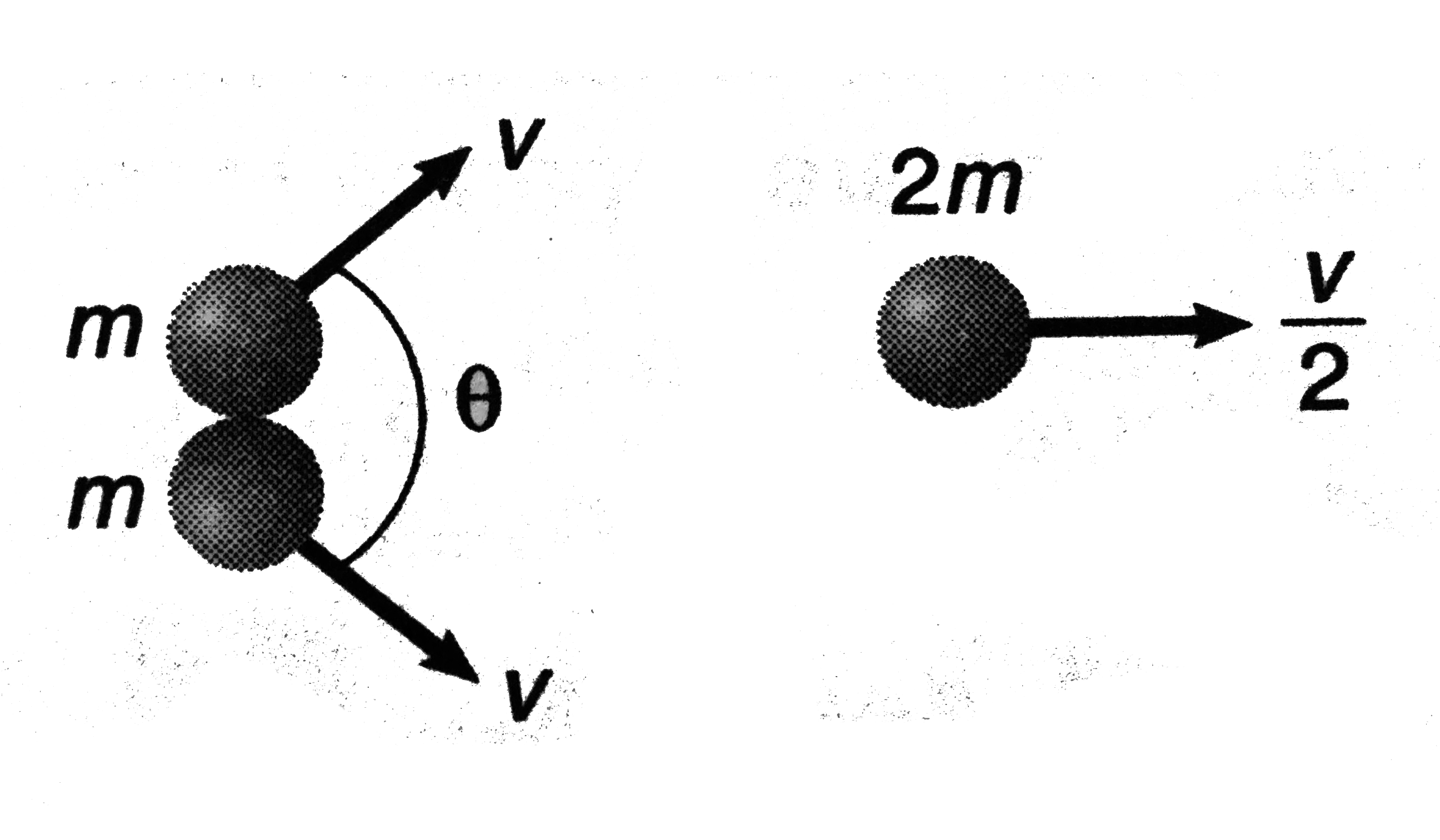
Hence, p2=p21+p22+2p2p2cosθ
or {2m(v2)}2=(mv)2+(mv)2+2(mv)(mv)cosθ
or 1=1+1+2cosθ or cosθ=−12
∴θ=120∘
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 11videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples13videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
After a totally inelastic collision, two objects of the same mass and same initial speeds are found to move together at half of their initial speeds. The angle between the initial velocities of the objects is
View SolutionAfter a totally inelastic collision, two objects of the same mass and same initial speeds are found to move together at half of their initial speeds. The angle between the initial velocities of the objects is
View SolutionAfter a totally inelastic collision, two objects of the same mass and same initial speeds are found to move together at half of their initial speeds. The angle between the initial velocities of the objects is
View SolutionAfter perfectly inelastic collision between two identical balls moving with same speed in different directions, the speed of the combined mass becomes half the initial speed. Find the angle between the two before collision.
View SolutionA particle of mass m is projected from the ground with an initial speed u0 at an angle α with the horizontal. At the highest point of its trajectory, it makes a completely inelastic collision with another identical particle, which was thrown vertically upward from the ground with the same initial speed u0. The angle that the composite system makes with the horizontal immediately after the collision is
View SolutionConsider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
View SolutionTwo stones are projected simultaneously from a tower a differenct angles of projection with same speed 'u'. The distance between two stones is increasing at constant rate 'u'. Then the angle between the initial velocity vectors of the two stones is :
View SolutionConsider the elastic collision f two bodies A and B of equal mass. Initially B is at rest and A moves with velocity v. After the collision -
View SolutionTwo particles of equal masses moving with same momentum collide perfectly inelastically. After the collision the combined mass moves with half of the speed of the individual masses. The angle between the initial momenta of individual particle is
View SolutionThe speed of a projectile at its maximum height is half of its initial speed. The angle of projection is .
View Solution

