In an inelastic collision (a) momentum of the system is always conserved (b) velocity of separation is less than the velocity of approach. (c) the coefficient of restitution can be zero. (d) All of the above
(a) momentum of the system is always conserved
(b) velocity of separation is less than the velocity of approach.
(c) the coefficient of restitution can be zero
(d) All of the above
The correct Answer is:D
To solve the question regarding inelastic collisions and determine which statements are correct, let's analyze each statement step by step.
Step 1: Understanding Inelastic Collisions
Inelastic collisions are defined as collisions where kinetic energy is not conserved, but momentum is conserved. This means that some kinetic energy is transformed into other forms of energy (like heat or sound) during the collision.
Step 2: Analyzing Statement (a)
Statement (a): "Momentum of the system is always conserved."
- In an inelastic collision, the total momentum before the collision equals the total momentum after the collision. Therefore, this statement is true.
Step 3: Analyzing Statement (b)
Statement (b): "Velocity of separation is less than the velocity of approach."
- The coefficient of restitution (e) is defined as the ratio of the relative velocity of separation to the relative velocity of approach. For inelastic collisions, this coefficient can be less than 1, and in some cases, it can be 0. Hence, the velocity of separation is indeed less than the velocity of approach. This statement is also true.
Step 4: Analyzing Statement (c)
Statement (c): "The coefficient of restitution can be zero."
- The coefficient of restitution can be zero in perfectly inelastic collisions, where the two colliding bodies stick together after the collision. Therefore, this statement is also true.
Step 5: Conclusion
Since all three statements (a), (b), and (c) are true, the correct answer is:
(d) All of the above.
Final Answer:
The correct option is (d) All of the above.
---
Inelastic collisions are defined as collisions where kinetic energy is not conserved, but momentum is conserved. This means that some kinetic energy is transformed into other forms of energy (like heat or sound) during the collision.
Statement (a): "Momentum of the system is always conserved."
- In an inelastic collision, the total momentum before the collision equals the total momentum after the collision. Therefore, this statement is true.
Statement (b): "Velocity of separation is less than the velocity of approach."
- The coefficient of restitution (e) is defined as the ratio of the relative velocity of separation to the relative velocity of approach. For inelastic collisions, this coefficient can be less than 1, and in some cases, it can be 0. Hence, the velocity of separation is indeed less than the velocity of approach. This statement is also true.
Statement (c): "The coefficient of restitution can be zero."
- The coefficient of restitution can be zero in perfectly inelastic collisions, where the two colliding bodies stick together after the collision. Therefore, this statement is also true.
Since all three statements (a), (b), and (c) are true, the correct answer is:
(d) All of the above.
The correct option is (d) All of the above.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective
32 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Assertion And Reason
15 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
STATEMENT-1 : In an elastic collision between two bodies, the relative velocity of separation equals relative velocity of approach.
and
STATEMENT-2 : In a elastic collision , the coefficient of restitution is 1.
View SolutionAssertion: For inelastic collision, 0≤e<1.
Reason: Hence, the magnitude of relative velocity of separation after collision is less than relative velocity of approach before collision.
View SolutionComprehension # 2
When two bodies collide normally they exert equal and opposite impulses on each other. Impulse = change in linear momentum. Coefficient of restitution between two bodies is given by :-
e=|Relative velocity of separation||Relative velocity of approach|=1, for elastic collision

Two bodies collide as shown in figure. During collision they exert impulse of magnitude J on each other.
For what value of J (in Ns ) the 2kg block will change its direction of velocity?
View SolutionComprehension # 2
When two bodies collide normally they exert equal and opposite impulses on each other. Impulse = change in linear momentum. Coefficient of restitution between two bodies is given by :- e=|Relative velocity of separation||Relative velocity of approach|=1, for elastic collision.
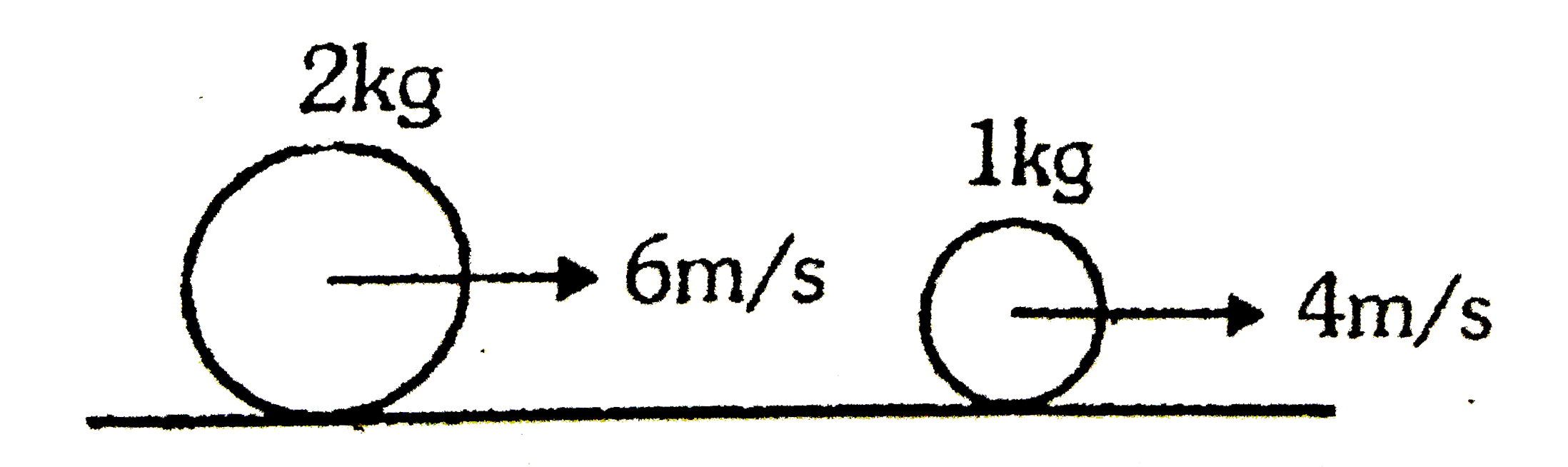
Two bodies collide as shown in figure. During collision they exert impulse of magnitude J on each other.
If the collision is elastic, the value of J is ............. Ns.
View SolutionA particle of mass m=1kg collides with the end with velocity v0=6ms−1 of a spinning rod of mass2m and length l=1m at the end of the rod. If the coefficient of restitution of collision e=(2/3), find the
a. velocity of the particle
b. angular velocity of the rod just after the impact.
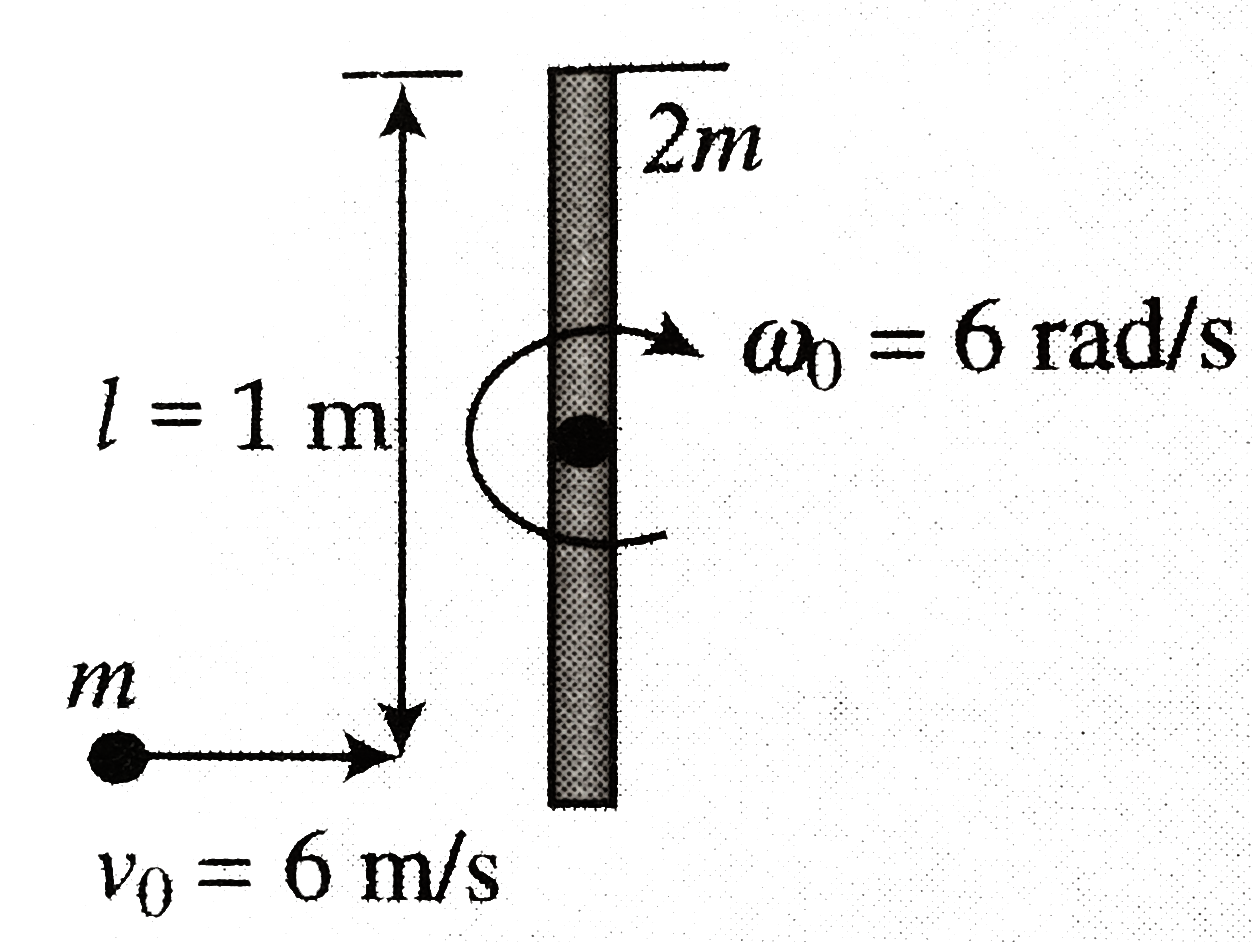
View SolutionA rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
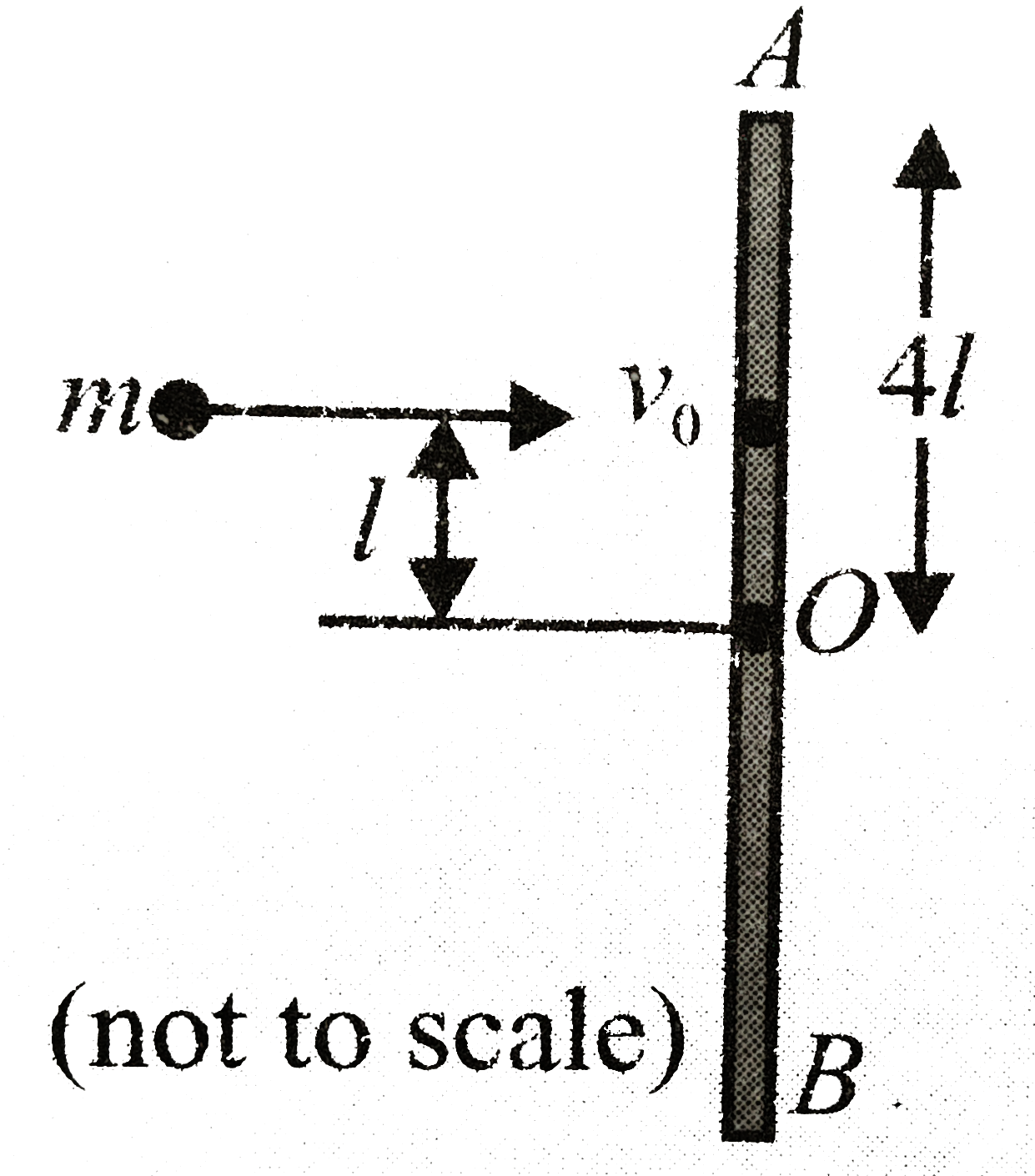
View SolutionAccording to the principle of conservation of linear momentum, if the external force acting on the system is zero, the linear momentum of the system will remain conserved. It means if the centre of mass of a system is initially at rest, it will remain, at rest in the absence of external force, that is, the displacement of centre of mass will be zero.
Two blocks of masses 'm'and '2m' are placed as shown in Fig. There is no friction anywhere. A spring of force constant k is attached to the bigger block. Mass 'm' is kept in touch with the spring but not attached to it. 'A' and 'B' are two supports attached to '2m'. Now m is moved towards left so that spring is compressed by distance 'x' and then the system is released from rest.

Find the relative velocity of the blocks after 'm' leaves contact with the spring.
View SolutionAnwer carefully, with reasons:
a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e. when they are in contact)?
Is the total linear momentum conserved during the short time of an elastic collision of two balls?
c) What are the answers to a) and b) for an inelastic collision?
d) If the potenital energy of two billiard balls depends only on the separation distance between their centers, is the collision elastic or inelastic? (note we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).
View SolutionA particle of mass 2kg moving with a velocity 5ˆim/s collides head-on with another particle of mass 3kg moving with a velocity −2ˆim/s. After the collision the first particle has speed of 1.6m/s in negative x-direction, Find
(a) velocity of the centre of mass after the collision,
(b) velocity of the second particle after the collision.
(c) coefficient of restitution.
View SolutionA particle of mass 2kg moving with a velocity 5ˆim/s collides head-on with another particle of mass 3kg moving with a velocity −2ˆim/s. After the collision the first particle has speed of 1.6m/s in negative x-direction, Find
(a) velocity of the centre of mass after the collision,
(b) velocity of the second particle after the collision.
(c) coefficient of restitution.
View Solution
