STATEMENT-1 : In an elastic collision between two bodies, the relative velocity of separation equals relative velocity of approach.
and
STATEMENT-2 : In a elastic collision , the coefficient of restitution is 1.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
Statement -1 is True, Statement-2 is True, Statement 2 is NOT a correct explanation for Statement-1
Statement-1 is True, Statement-2 is False
Statement-1 is False, Statement-2 is True
To solve the question, we need to analyze both statements regarding elastic collisions and the coefficient of restitution.
1. Understanding Elastic Collisions:
- In an elastic collision, both momentum and kinetic energy are conserved. This means that the total momentum and the total kinetic energy before and after the collision remain the same.
2. Relative Velocity of Approach and Separation:
- The relative velocity of approach is defined as the velocity of one body with respect to another before the collision.
- The relative velocity of separation is defined as the velocity of one body with respect to another after the collision.
- For two bodies colliding elastically, the relative velocity of separation equals the negative of the relative velocity of approach.
3. Coefficient of Restitution:
- The coefficient of restitution (denoted as e) is defined as the ratio of the relative velocity of separation to the relative velocity of approach.
- Mathematically, this can be expressed as:
\(
e = \frac{\text{Velocity of separation}}{\text{Velocity of approach}}
\)
- For elastic collisions, the value of e is equal to 1.
4. Analyzing Statement 1:
- Statement 1 claims that in an elastic collision, the relative velocity of separation equals the relative velocity of approach.
- Since we know that for elastic collisions, the relative velocity of separation is equal to the relative velocity of approach (with a sign change), this statement is true.
5. Analyzing Statement 2:
- Statement 2 states that in an elastic collision, the coefficient of restitution is 1.
- This is a fundamental property of elastic collisions, confirming that this statement is also true.
6. Conclusion:
- Both statements are true.
- Furthermore, Statement 2 provides the correct explanation for Statement 1 because it establishes the condition under which the relative velocities are equal.
Final Answer:
- Statement 1 is true.
- Statement 2 is true, and it is the correct explanation for Statement 1.
- In an elastic collision, both momentum and kinetic energy are conserved. This means that the total momentum and the total kinetic energy before and after the collision remain the same.
- The relative velocity of approach is defined as the velocity of one body with respect to another before the collision.
- The relative velocity of separation is defined as the velocity of one body with respect to another after the collision.
- For two bodies colliding elastically, the relative velocity of separation equals the negative of the relative velocity of approach.
- The coefficient of restitution (denoted as e) is defined as the ratio of the relative velocity of separation to the relative velocity of approach.
- Mathematically, this can be expressed as:
\(
e = \frac{\text{Velocity of separation}}{\text{Velocity of approach}}
\)
- For elastic collisions, the value of e is equal to 1.
- Statement 1 claims that in an elastic collision, the relative velocity of separation equals the relative velocity of approach.
- Since we know that for elastic collisions, the relative velocity of separation is equal to the relative velocity of approach (with a sign change), this statement is true.
- Statement 2 states that in an elastic collision, the coefficient of restitution is 1.
- This is a fundamental property of elastic collisions, confirming that this statement is also true.
- Both statements are true.
- Furthermore, Statement 2 provides the correct explanation for Statement 1 because it establishes the condition under which the relative velocities are equal.
- Statement 1 is true.
- Statement 2 is true, and it is the correct explanation for Statement 1.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - F) Matrix-Match Type Questions
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - G) Integar Type Questions
10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
20 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
In an elastic collision between two particles
View SolutionSTATEMENT-l : In an elastic collision between two bodies, the relative speed of the bodies after collision is equal to the relative speed before the collision.
STATEMENT-2 : In an elastic collision, the linear momentum of the system is conserved.
View Solution
Knowledge Check
In an elastic one dimensional collision between two particles the relative veloctiy of approach before collision is
Agreater than the relative velocity of separation after collisionBless than the relative velocity of separation after collisionCequal to the relative velocity of separation after collisionDless than the relative velocity of separation if the incoming particle is heavier than the target particle
In a head on elastic collision of two bodies of equal masses
View SolutionStatement I: In an elastic collision between two bodies, the relative speed of the bodies after collision is equal to the relative speed before the collision.
Statement II: In an elastic collision, the linear momentum of the system is conserved.
View SolutionIn an inelastic collision (a) momentum of the system is always conserved (b) velocity of separation is less than the velocity of approach. (c) the coefficient of restitution can be zero. (d) All of the above
View SolutionComprehension # 2
When two bodies collide normally they exert equal and opposite impulses on each other. Impulse = change in linear momentum. Coefficient of restitution between two bodies is given by :- e=|Relative velocity of separation||Relative velocity of approach|=1, for elastic collision.
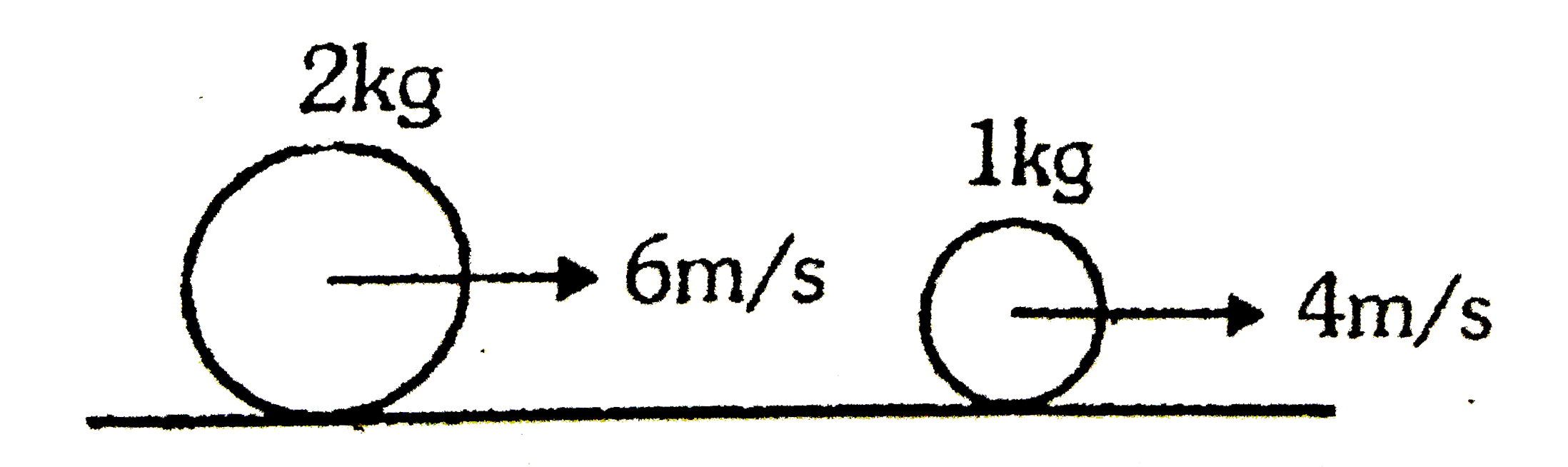
Two bodies collide as shown in figure. During collision they exert impulse of magnitude J on each other.
If the collision is elastic, the value of J is ............. Ns.
View SolutionComprehension # 2
When two bodies collide normally they exert equal and opposite impulses on each other. Impulse = change in linear momentum. Coefficient of restitution between two bodies is given by :-
e=|Relative velocity of separation||Relative velocity of approach|=1, for elastic collision

Two bodies collide as shown in figure. During collision they exert impulse of magnitude J on each other.
For what value of J (in Ns ) the 2kg block will change its direction of velocity?
View SolutionSTATEMENT-1 : In an elastic collision between two balls, the total kinetic energy of the two bodies does not remain conserved during the collision.
and
STATEMENT-2 : As the balls collide, they compress each other.
View SolutionAssertion: For inelastic collision, 0≤e<1.
Reason: Hence, the magnitude of relative velocity of separation after collision is less than relative velocity of approach before collision.
View Solution
