A small body of mass 'm' is placed at the top of a smooth sphere of radius 'R' placed on a horizontal surface as shown, Now the sphere is given a constant horizontal acceleration $a_{0} = g$ . The velocity of the body relative to the sphere at the moment when it loses contact with the sphere is

A

$\sqrt{\frac{g R}{3}}$

B

$\sqrt{\frac{2 g R}{3}}$

C

$\sqrt{\frac{5 g R}{3}}$

D

$\sqrt{\frac{7 g R}{3}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let v is the velocity of the body relative to the sphere when it loses contact with the sphere.
$m g cos θ - N - m a_{0} sin θ \frac{m v^{2}}{R}$
To lose contact with the sphere, $N = 0$
$m g cos θ - m a_{0} sin θ = \frac{m v^{2}}{R}$
Also, $m g R (1 - cos θ) + m a_{0} R sin h η = \frac{1}{2} m v^{2}$
$m g = \frac{3 m v^{2}}{2 R}$
$∴ v = \sqrt{\frac{2 g R}{3}}$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

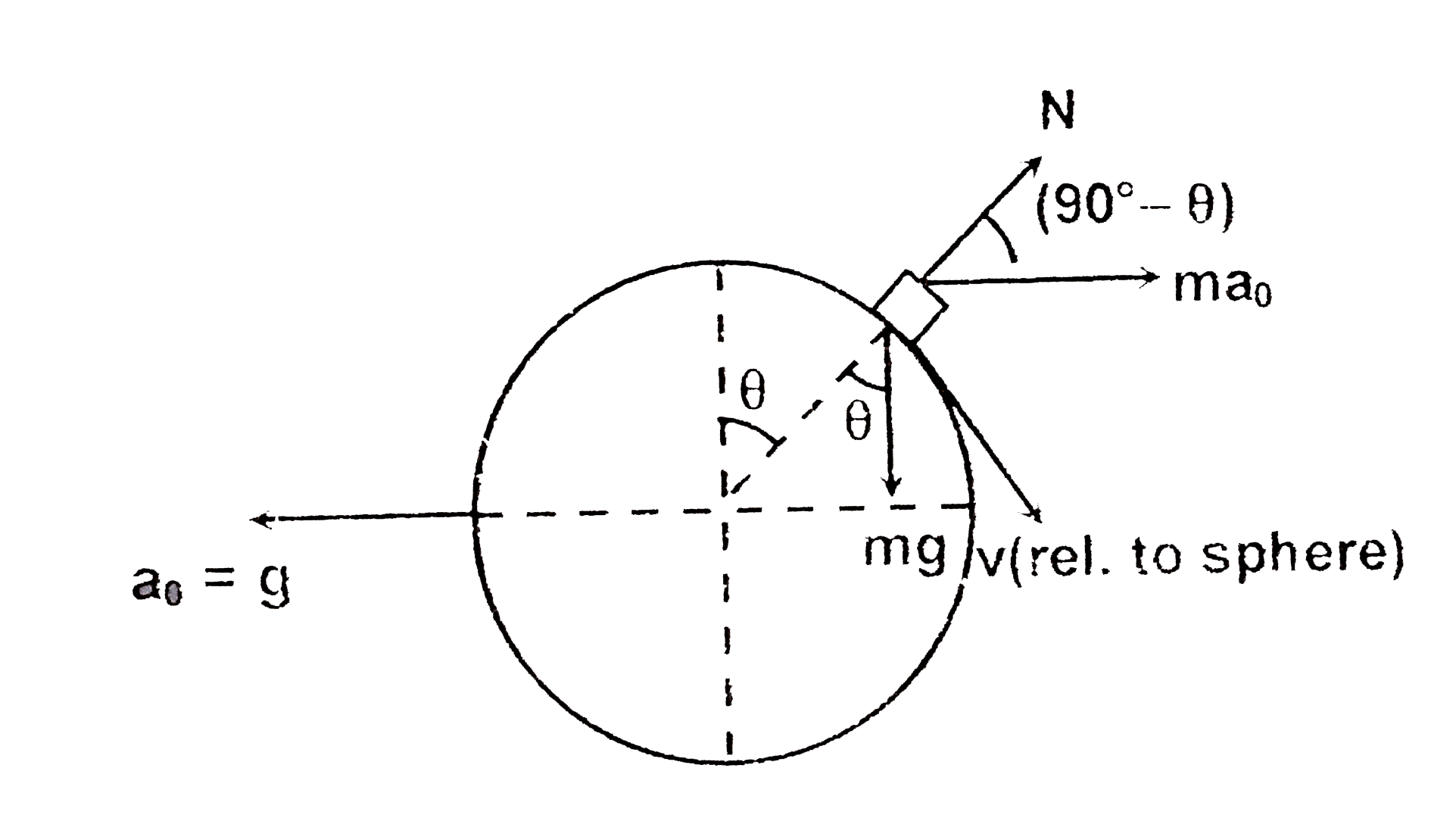
Similar Questions

Recommended Questions

Home
Ask Doubt
Profile