
Rod AB has length L. velocity of end A of the rod has velocity υ0 at the given instant.
(a). Which type of motion the rod has?
(b). Find velocity of end B at the given instant.
(C). Find the angular velocity of the rod.

(a). The rod has rotational plus translational motion.
(b). Let velocity of end B is VB is the direction shown in figure.
Components of VA and VB along AB and perpendicular to AB are also shown in the same figure.
Rod is a rigid body. so, distance AB should remain constant or the components along AB should be same.
(c). 
Perpendicular to AB, components will be
vr=v02+√3vB2
substituting vB=√3v0 we get vr=2v0
Now angular velocity of the rod is ω=vrAB
or ω=2voL
Rotation of the rod is anticlockwise. Therefore, from right hand rule ω is perpendicular to paper outwards or in ⊙ direction.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples25videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
The velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is
 View Solution
View SolutionA rod AB is placed on smooth inclined plane as shown in the figure. At the instant which is shown in the figure, the angular velocity of the rod is
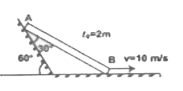 View Solution
View SolutionThe instaneous velocity of point B of the given rod of length 0.5 is 3m/s in the represented direction. The angualr velocity of the rod for minimum velocity of end A is
 View Solution
View SolutionIn the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be
 View Solution
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionTwo points of a rod move with velocity 3v and v perpendicular to the rod and in the same direction. Separated by a distance r. Then the angular velocity of the rod is :
View SolutionA rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
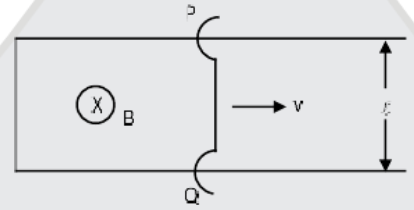 View Solution
View SolutionA rod AB of mass M and length 8l lies on a smooth horizontal surface. A particle, of mass m and velocity v0 strike's the rod perpendicular to its length, as shown in Fig. As a result of the collision, the centre of mass of the rod attains a speed of v0/8 and the particle rebounds back with a speed of v0/4. Find the following: a. The ratio M/m. b. The angular velocity of the rod about O. c. The coefficient of restitution 'e' for the collision. d. The velocities of the ends 'A' and 'B' of the rod, namely, vA and vB respectively.
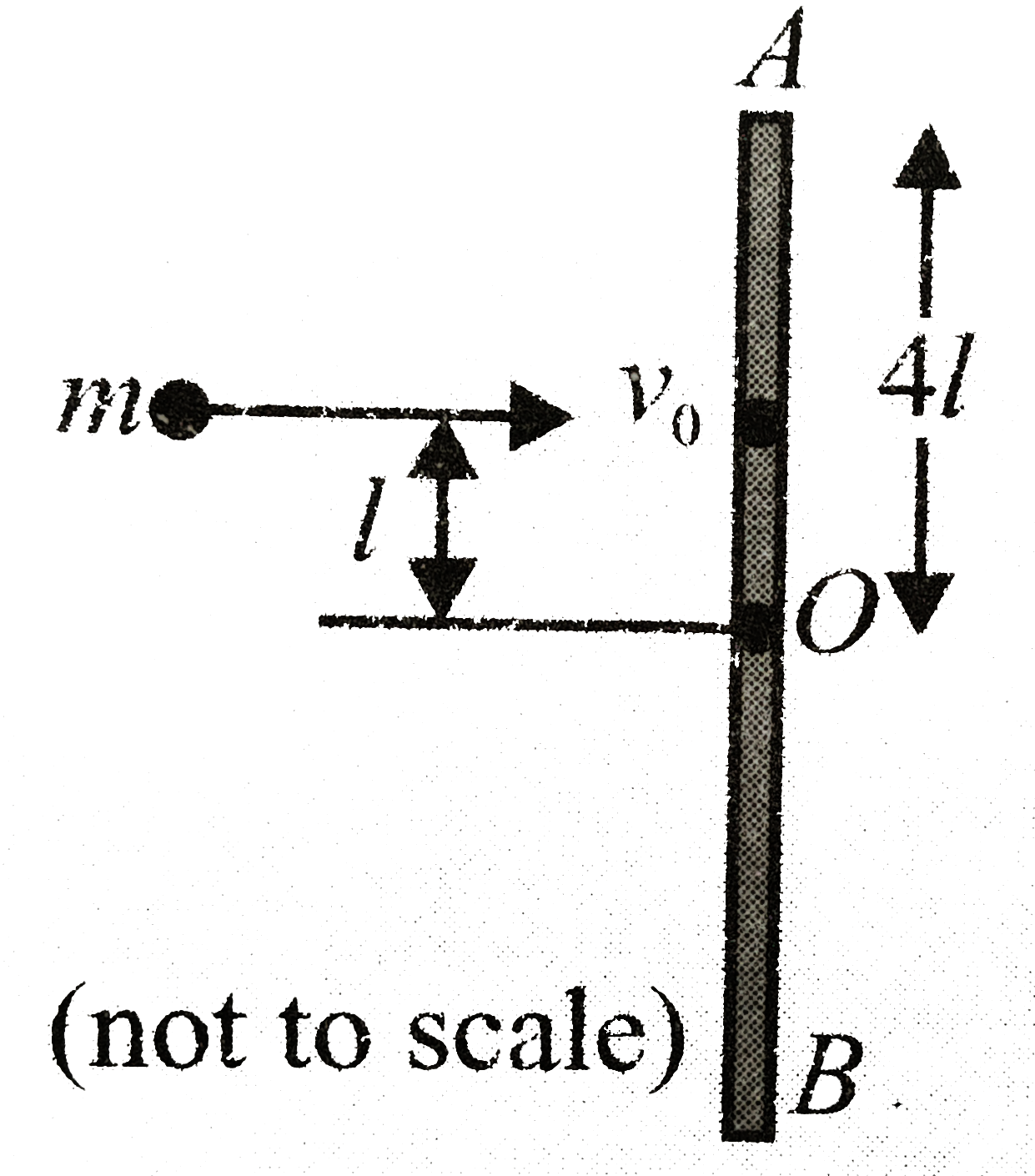 View Solution
View SolutionA uniform rod PQ of mass m and length t rotates with an angular velocity a while its center moves with linear velocity v=2ω⋅f3 on a smooth horizontal surface If the end Q of the rod is suddenly gets stuck at the moment as shown in the figure then angular velocity of the rod will be
View SolutionThe end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity v0 as shown. The length of the rod is l. At the instant when θ=37∘
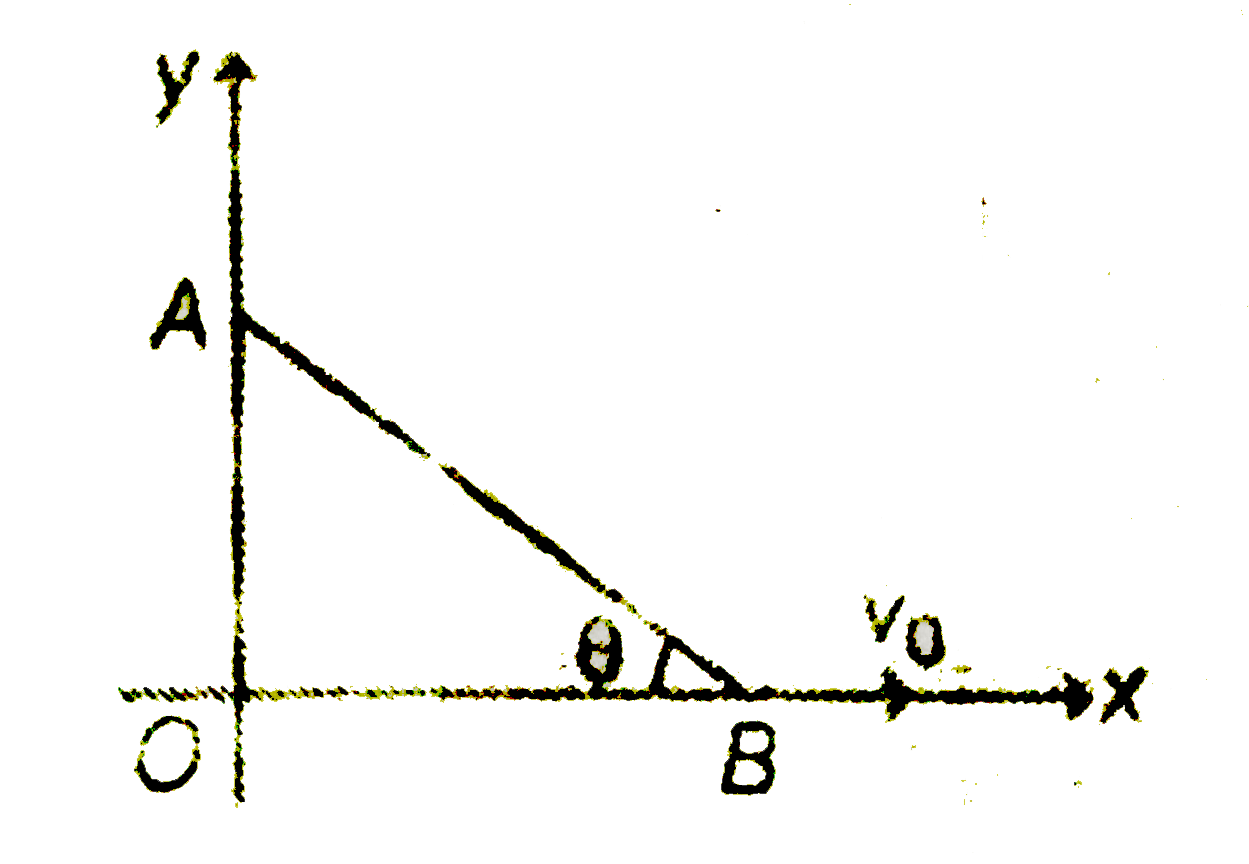
(A)velocity of end A is 43v0 downwards
(B)angular velocity of rod is 53v0l
(C)angular velocity of rod is constant
(D)velocity of end A is constantView Solution

