A man pushes a cylinder of mass m1 with the help of a plank of mass m2 as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
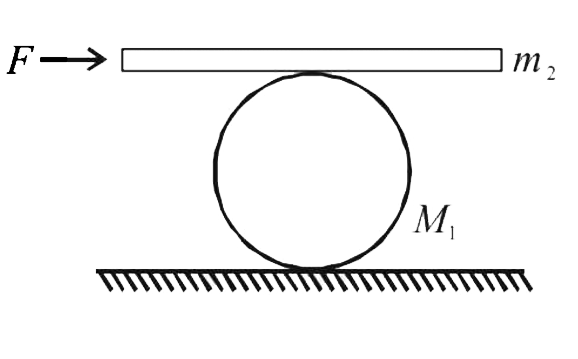
(b) the magnitudes and direction of frictional force at contact points.

We can choose any arbitrary direction of frictional forces at different contacts.
In the final answer, the negative value will show for opposite direction
let f1= friction between plank and cylinder
f2= friction between cylinder and ground
a1= acceleration of plank
a2= acceleration of centre of mass of cylinder
and α= angular acceleration of cylinder about is COM.

Decreation of f1 and f2 are as shown here.
Since, there is not slipping anywhere
∴a1=2a2 ..(i)
(acceleration of plank = acceleration fo top point of cylinder)
a1=F−f1m2 ...(ii)
a2=f1+f2m1
α(f1−f2)RI
(I= moment of inertia of cylinder about COM)

∴α=(f1−f2)R12m1R2
α=(2f1−f2m1R ..(iv)
a2=Rα(2f1−f2m1 ....(v)
(acceleration of bottommost point of cylinder =0)
(a). solving eqs (i), (ii), (iii) and (V) we get
a1=8F3m1+8m2
and a2=4F3m1+8m2
(b). f1=m1F3m1+8m2
Since all quantities are positive, they are correctly shown in figures.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 21videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions

A cylinder is sandwiched between two planks. Two constant horizontal forces F and 2F are applied on the planks as shown. Determine the acceleration of the centre of mass of cylinder and the top plank. If there is no slipping at the top and bottom of cylinder.View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.When a horizontal force F is applied at centre of sphere, acceleration of the plank is

View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank isView SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.
 View Solution
View SolutionConsider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in the figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point to contact.

(a) what are the directions of the fricition forces acting at A and B on the plank and the cylinder ?
(b) Calculate the acceleration of the cylinder.
(c) Find the value of frictional force at A & B.View SolutionA plank of mass M is placed on a rough horizontal surface and a contant horizontal force F is applied on it . A man of mass m runs on the plank find the range of acceleration of the man that the plank does not move on the surface is μ .Assume that the does not slip on the plank
 View Solution
View SolutionA man of mass m moves on a plank of mass M with a constant velocity u with respect to the plank, as shown in figure.
a.If the plank rests on smooth horizontal surface, determine the velocity of the plank. .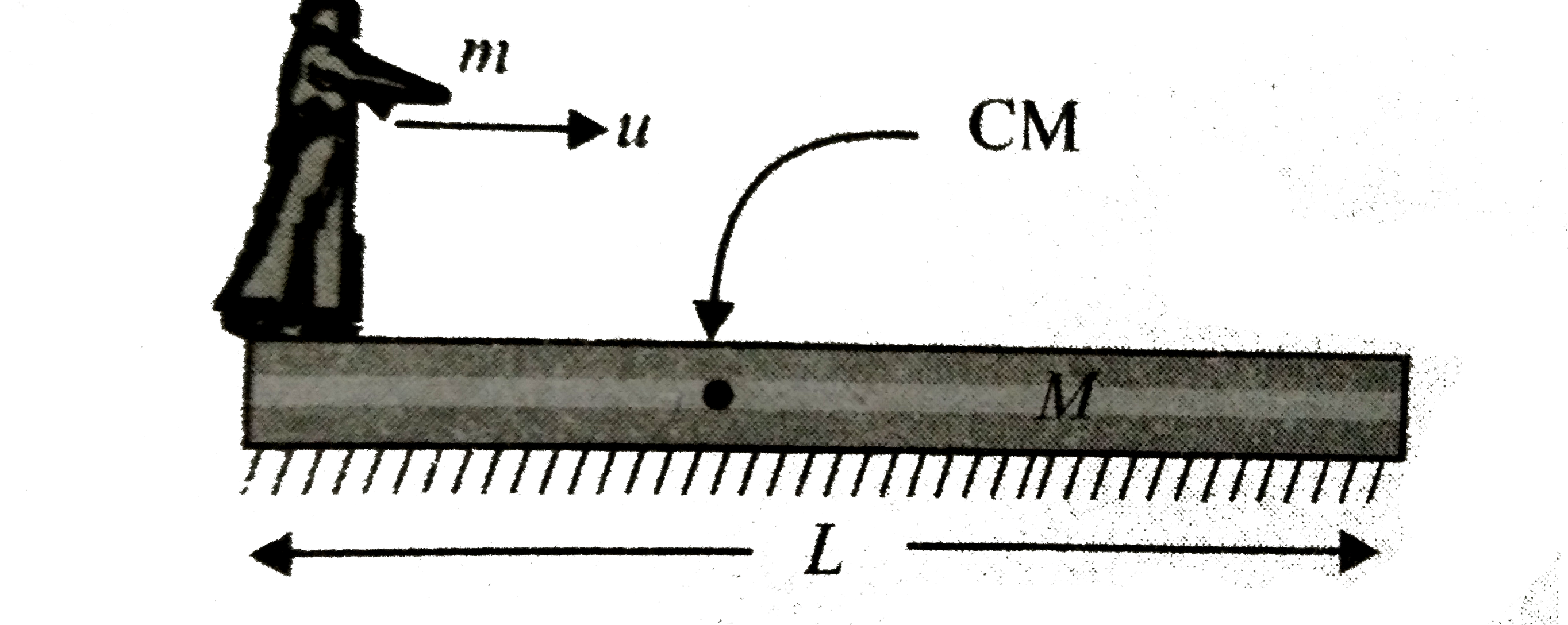 View Solution
View SolutionA man of mass m is standing at one end of of a plank of mass M. The length of the plank is L and it rests on a frictionless horizontal ground. The man walks to the other end of the plank. Find displacement of the plank and man relative to the ground.
 View Solution
View SolutionA small block B of mass m2 is placed on another block A of mass m1 A constant horizontal force F is applied to the block A. All the surfaces are assumed to be frictionless. Find the acceleration of center of mass of the system
View Solution
A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isView Solution

