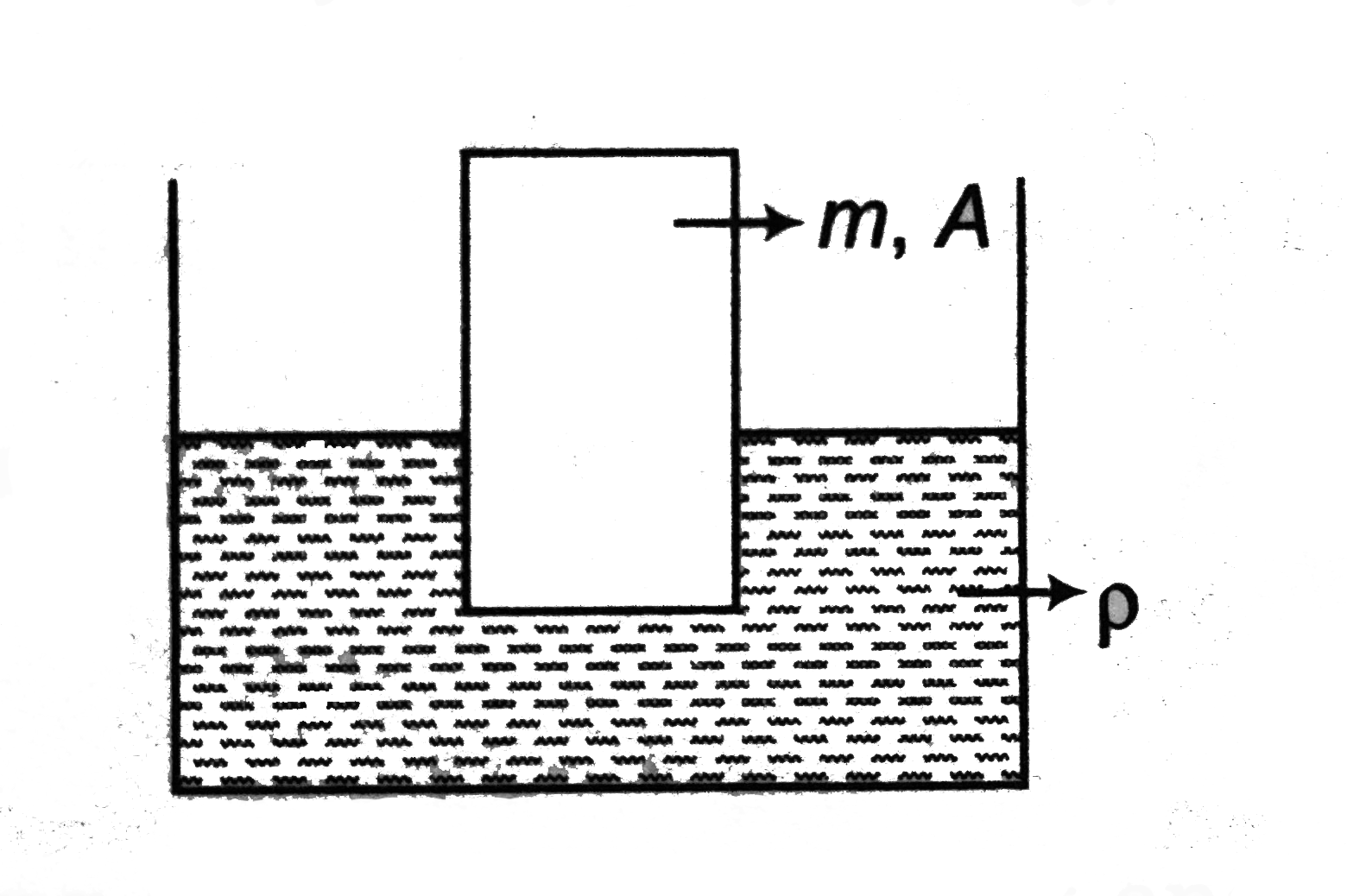
A plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
The correct Answer is:A, B
Two forces are action on the plank: weight and upthrust. Weight is a constant force. So, forget it. Upthrust (if partially immersed ) is a variable force. When displaced downwards by a distance x, then
Net restoring forceF≠t=−[change or increase in variable force upthrust]
= - [(extra immersed volume) (density of liquid) (g)]
=−[(Ax)(ρ)(g)]
This force is of type F=−kx
So, motion is simple harmonic, where k=ρAg
∴T=2π√mk or T=2π√mρAg.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Miscellaneous Examples
8 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 12
1 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these oscillations.

View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View Solution
Knowledge Check
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝1√mBT∝√ρCT∝1√ADT∝1ρ
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View SolutionA cylindrical block of wood of mass m and area cross-section A is floating in water (density = ρ) when its axis vertical. When pressed a little and the released the block starts oscillating. The period oscillations is
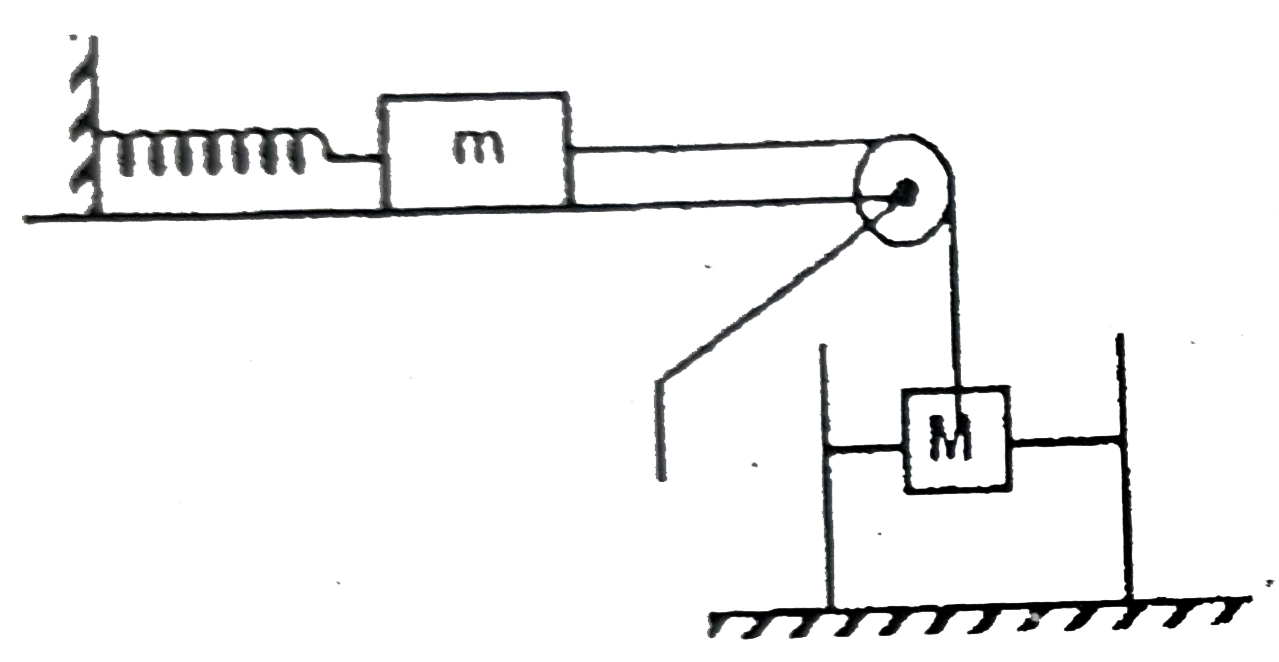
View SolutionFor the arrangement shown, a cylinder of mass m with cross-sectional area A, initially in equilibrium poisition, is displaced slightly inside the liquid of density p. Prove that the motion is simple harmonic and also find its time-period.
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is givan a small vertical displacement from equilibrium, it undergoes oscillation with a time period T, then select the wrong alternative.
View SolutionA block of rectangular size of mass m and area of cross section A, float in a liquid of density ρ.If we give a small vertical displacement from equilibrium, It undergoes SHM with time period T, then
View SolutionA plank of area of cross-section A is half immersed in liquid 1 of density ρ and half in liquid 2 of density 2ρ. What is period of osciallation of the plank if it is slightly depressed downwards?

View SolutionIs oscillation of a mass suspended by a spring simple harmonic ? give expression for its time period also.
View Solution
