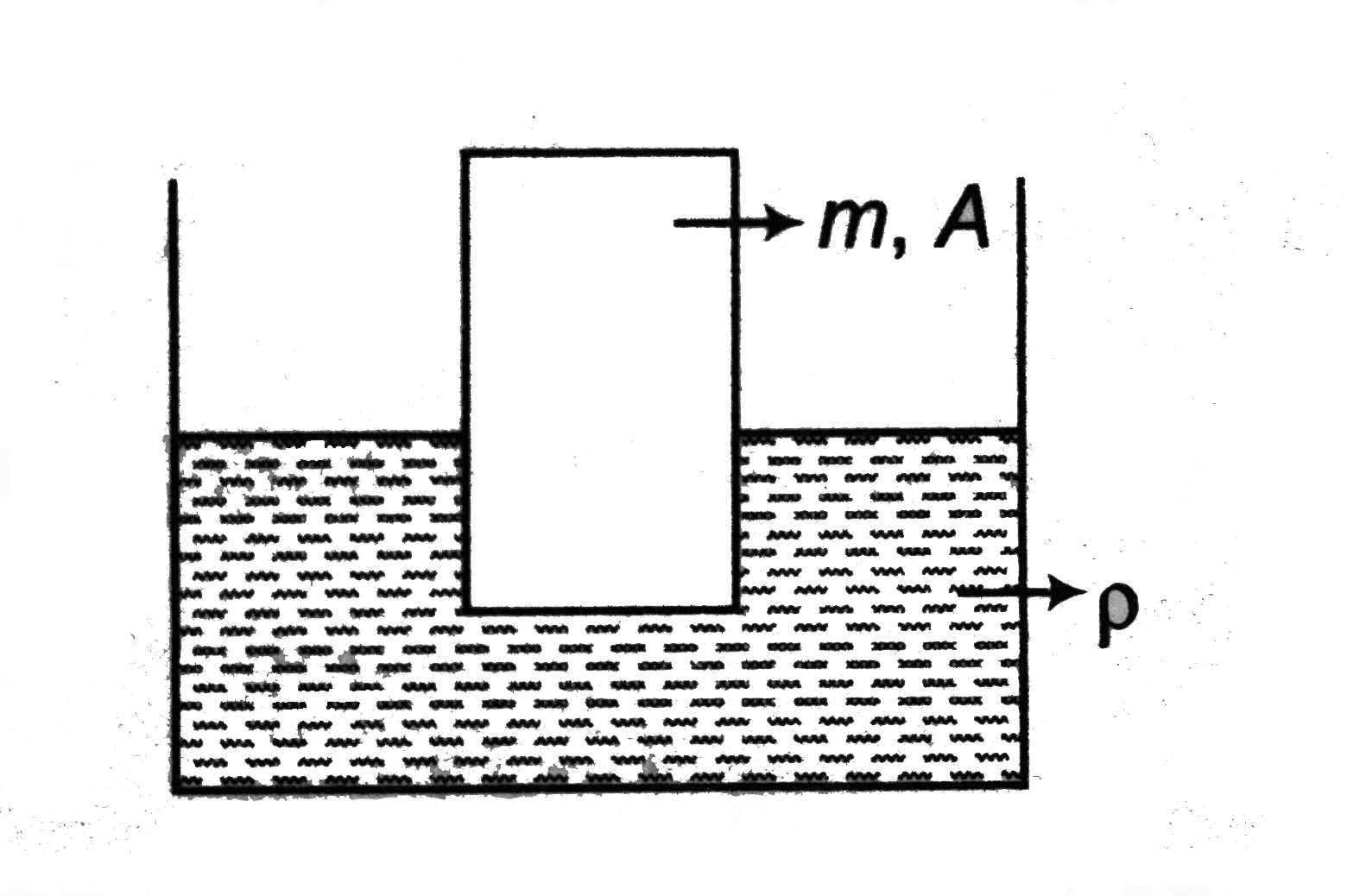
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is givan a small vertical displacement from equilibrium, it undergoes oscillation with a time period T, then select the wrong alternative.
T2αm
T2αg
T2α1/A
T2α1ρ
The correct Answer is:B
To solve the problem step by step, we will analyze the given information about the rectangular block floating in a liquid and derive the time period of oscillation.
Step 1: Understand the equilibrium condition
When the block is floating in the liquid, the buoyant force acting on it is equal to its weight. According to Archimedes' principle, the buoyant force Fb is given by:
Fb=ρ⋅V⋅g
where ρ is the density of the liquid, V is the volume of the liquid displaced, and g is the acceleration due to gravity.
Step 2: Relate volume to area and length
The volume V of the block can be expressed in terms of its cross-sectional area A and the submerged length l:
V=A⋅l
Thus, the buoyant force can be rewritten as:
Fb=ρ⋅(A⋅l)⋅g
Step 3: Set up the equilibrium equation
At equilibrium, the weight of the block mg is balanced by the buoyant force:
mg=ρ⋅(A⋅l)⋅g
From this, we can simplify and solve for l:
l=mgρAg=mρA
Step 4: Determine the time period of oscillation
For small vertical displacements, the time period T of oscillation can be derived from the formula:
T=2π√lg
Substituting the expression for l:
T=2π√mρAg
Step 5: Analyze the relationships
From the derived formula for T:
- T2 is directly proportional to m (mass of the block).
- T2 is inversely proportional to A (area of cross-section).
- T2 is inversely proportional to ρ (density of the liquid).
- T2 is inversely proportional to g (acceleration due to gravity).
Step 6: Identify the wrong alternative
Based on the relationships derived:
1. T2 is directly proportional to m - True
2. T2 is directly proportional to g - False (it is inversely proportional)
3. T2 is inversely proportional to A - True
4. T2 is inversely proportional to ρ - True
Thus, the wrong alternative is option 2.
When the block is floating in the liquid, the buoyant force acting on it is equal to its weight. According to Archimedes' principle, the buoyant force Fb is given by:
Fb=ρ⋅V⋅g
where ρ is the density of the liquid, V is the volume of the liquid displaced, and g is the acceleration due to gravity.
The volume V of the block can be expressed in terms of its cross-sectional area A and the submerged length l:
V=A⋅l
Thus, the buoyant force can be rewritten as:
Fb=ρ⋅(A⋅l)⋅g
At equilibrium, the weight of the block mg is balanced by the buoyant force:
mg=ρ⋅(A⋅l)⋅g
From this, we can simplify and solve for l:
l=mgρAg=mρA
For small vertical displacements, the time period T of oscillation can be derived from the formula:
T=2π√lg
Substituting the expression for l:
T=2π√mρAg
From the derived formula for T:
- T2 is directly proportional to m (mass of the block).
- T2 is inversely proportional to A (area of cross-section).
- T2 is inversely proportional to ρ (density of the liquid).
- T2 is inversely proportional to g (acceleration due to gravity).
Based on the relationships derived:
1. T2 is directly proportional to m - True
2. T2 is directly proportional to g - False (it is inversely proportional)
3. T2 is inversely proportional to A - True
4. T2 is inversely proportional to ρ - True
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:JEE Advanced
Explore 34 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:More than one option is correct
Explore 50 Videos
- SIMPLE HARMONIC MOTIONBook:DC PANDEY ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Exercise 14.4
Explore 4 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBook:DC PANDEY ENGLISHChapter:SEMICONDUCTORS AND ELECTRONIC DEVICESExercise:More than One Option is Correct
Explore 3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBook:DC PANDEY ENGLISHChapter:SOLVD PAPERS 2017 NEET, AIIMS & JIPMERExercise:Solved paper 2018(JIPMER)
Explore 38 Videos
Similar Questions
A block of rectangular size of mass m and area of cross section A, float in a liquid of density ρ.If we give a small vertical displacement from equilibrium, It undergoes SHM with time period T, then
View SolutionA plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these oscillations.

View SolutionA cylindrical block of wood of mass m and area cross-section A is floating in water (density = ρ) when its axis vertical. When pressed a little and the released the block starts oscillating. The period oscillations is
View SolutionA plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
View SolutionA plank of area of cross-section A is half immersed in liquid 1 of density ρ and half in liquid 2 of density 2ρ. What is period of osciallation of the plank if it is slightly depressed downwards?

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
A thin-walled tube of mass m and radius R has a rod of mass m and vry small cross section soldered on its inner surface. The side-view of the arrangement is as shown in the following figure. The entire arrangement is placed on a rough horizontal surface. The system is given a small angular displacement from its equilibrium position, as a result, the system performs oscillations. The time period of resulting oscillations if the tube rolls without slipping is
View SolutionA small ring of mass m1 is connected by a string of length l to a small heavy bob of mass m2. The ring os free to move (slide) along a fixed smooth horizontal wire. The bob is given a small displacement from its equilibrium position at right angles to string. Find period of small oscillations.
_E01_106_Q01.png)
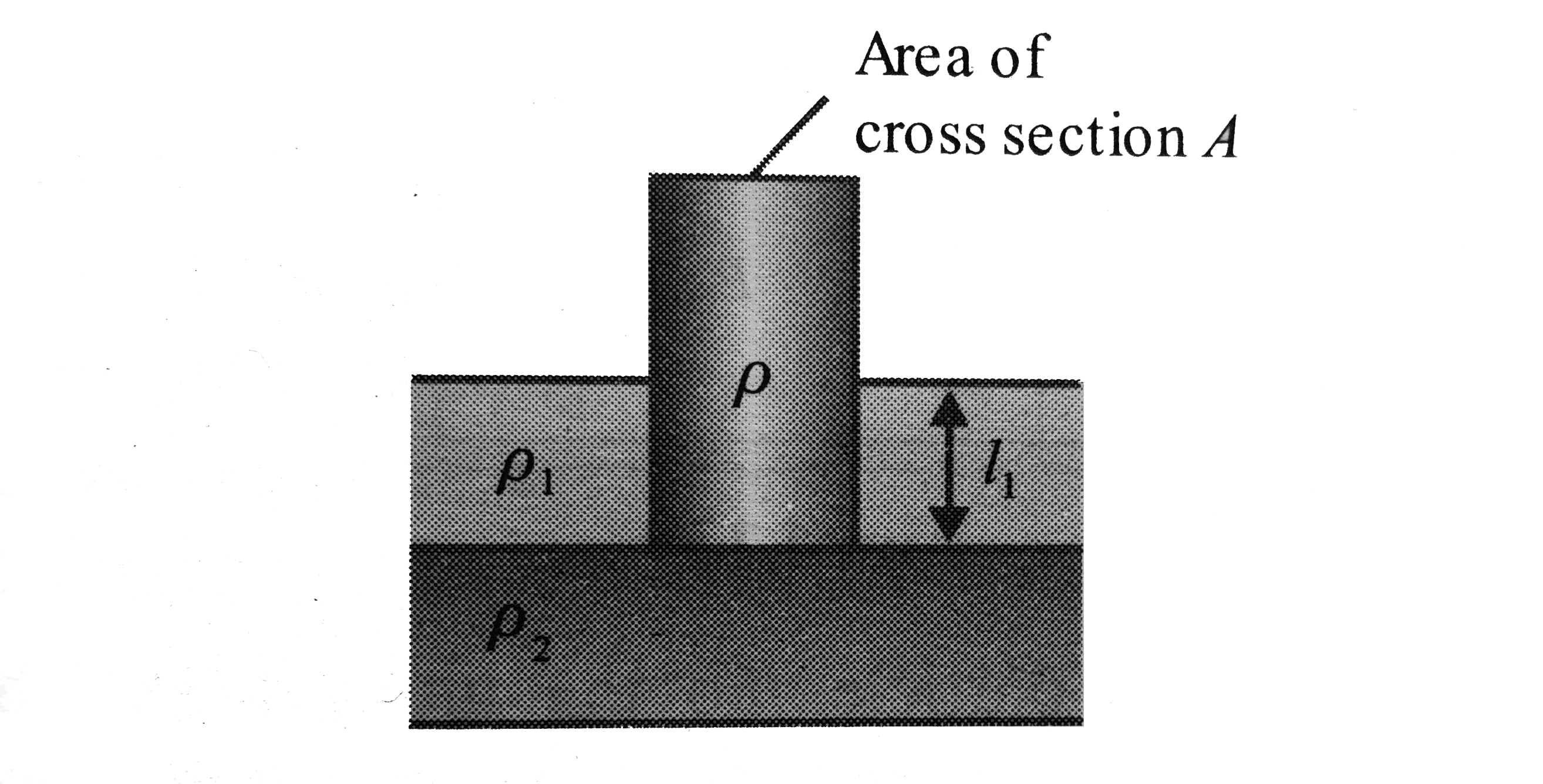
View SolutionA vertical pole of length l , density ρ , area of cross section A floats in two immiscible liquids of densities ρ1and ρ2. In equuilibrium possition the bottom end is at the interface of the liquids. When the cylinder is displaced vertically, find the time period of oscillation.
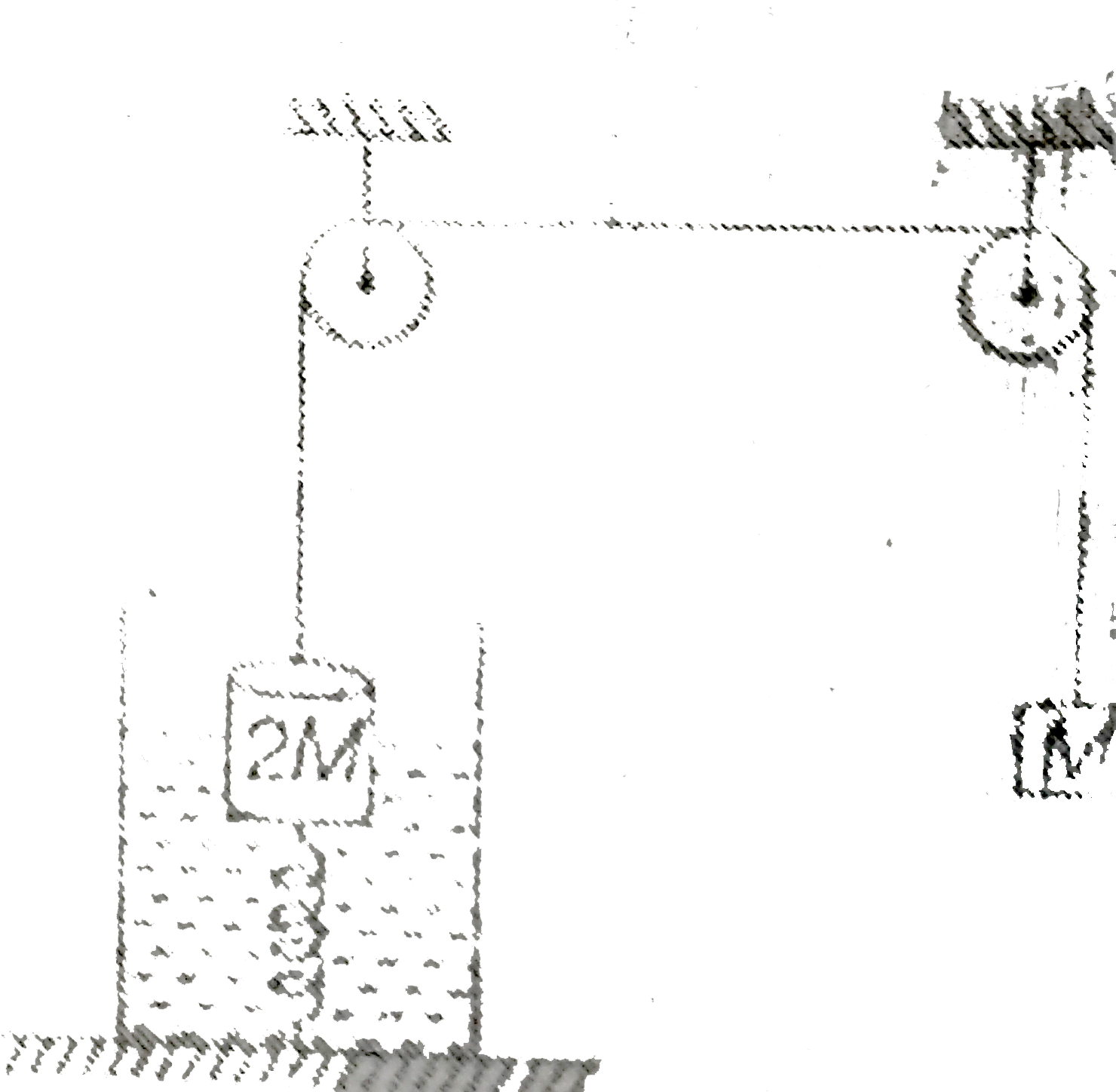
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
Under equilibrium conditions
View Solution
