A cylindrical block of wood of mass m and area cross-section A is floating in water (density = ρ) when its axis vertical. When pressed a little and the released the block starts oscillating. The period oscillations is
(2π√mρbg
2π√mgρA
2π√ρAgm
2π√ρAmg)
The correct Answer is:A
To find the period of oscillation of a cylindrical block of wood floating in water, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
When the block is floating, it experiences two main forces:
- The weight of the block (W = mg, acting downwards)
- The buoyant force (F_b, acting upwards)
At equilibrium, the buoyant force equals the weight of the block:
Fb=W
Fb=ρwater⋅Vsubmerged⋅g
Where Vsubmerged=A⋅h (A is the area of cross-section and h is the height submerged).
Step 2: Write the Equilibrium Condition
At equilibrium, we can express:
ρwater⋅A⋅h⋅g=mg
This gives us the relationship between the submerged height and the mass of the block.
Step 3: Consider the Displacement
When the block is pressed down slightly and then released, it will oscillate. Let x be the additional displacement from the equilibrium position. The new submerged height becomes h+x.
Step 4: Calculate the New Buoyant Force
The new buoyant force when the block is displaced by x is:
F′b=ρwater⋅A⋅(h+x)⋅g
F′b=ρwater⋅A⋅h⋅g+ρwater⋅A⋅x⋅g
Step 5: Find the Net Force
The net force F acting on the block when displaced is:
F=W−F′b
Substituting the expressions we have:
F=mg−(ρwater⋅A⋅h⋅g+ρwater⋅A⋅x⋅g)
Using the equilibrium condition Fb=mg, we can simplify:
F=−ρwater⋅A⋅g⋅x
Step 6: Relate to Simple Harmonic Motion
This net force can be expressed in the form of Hooke's Law:
F=−kx
Where k=ρwater⋅A⋅g.
Step 7: Find the Time Period
The time period T of oscillation for a mass-spring system is given by:
T=2π√mk
Substituting for k:
T=2π√mρwater⋅A⋅g
Final Answer
The period of oscillation of the cylindrical block of wood floating in water is:
T=2π√mρwater⋅A⋅g
---
When the block is floating, it experiences two main forces:
- The weight of the block (W = mg, acting downwards)
- The buoyant force (F_b, acting upwards)
Fb=W
Fb=ρwater⋅Vsubmerged⋅g
Where Vsubmerged=A⋅h (A is the area of cross-section and h is the height submerged).
At equilibrium, we can express:
ρwater⋅A⋅h⋅g=mg
This gives us the relationship between the submerged height and the mass of the block.
When the block is pressed down slightly and then released, it will oscillate. Let x be the additional displacement from the equilibrium position. The new submerged height becomes h+x.
The new buoyant force when the block is displaced by x is:
F′b=ρwater⋅A⋅(h+x)⋅g
F′b=ρwater⋅A⋅h⋅g+ρwater⋅A⋅x⋅g
The net force F acting on the block when displaced is:
F=W−F′b
Substituting the expressions we have:
F=mg−(ρwater⋅A⋅h⋅g+ρwater⋅A⋅x⋅g)
Using the equilibrium condition Fb=mg, we can simplify:
F=−ρwater⋅A⋅g⋅x
This net force can be expressed in the form of Hooke's Law:
F=−kx
Where k=ρwater⋅A⋅g.
The time period T of oscillation for a mass-spring system is given by:
T=2π√mk
Substituting for k:
T=2π√mρwater⋅A⋅g
The period of oscillation of the cylindrical block of wood floating in water is:
T=2π√mρwater⋅A⋅g
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Advanced
34 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise 14.4
4 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A cylindrical block of wood of mass M is floating n water with its axis vertica. It is depressed a little and then released. Show that the motion of the block is simple harmonic and find its frequency.
View SolutionA plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these oscillations.

View Solution
Knowledge Check
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
AT∝1√mBT∝√ρCT∝1√ADT∝1ρ
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View SolutionA plank of mass 'm' and area of cross - section A is floating in a non - viscous liquid of desity ρ. When displaced slightly from the mean position, it starts oscillating. Prove that oscillations are simple harmonic and find its time period.
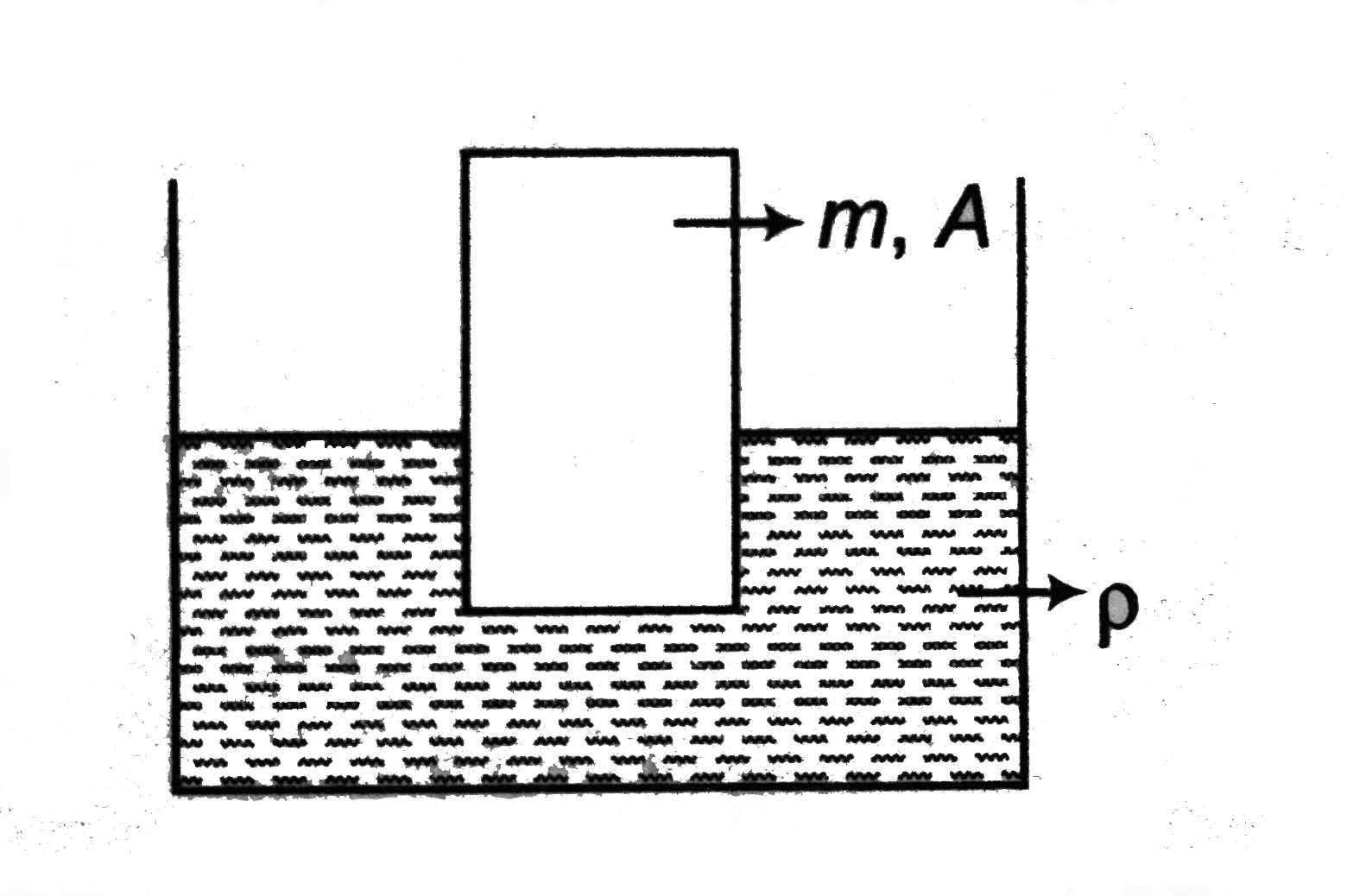
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is givan a small vertical displacement from equilibrium, it undergoes oscillation with a time period T, then select the wrong alternative.
View SolutionA wire of length l, area of cross-section A and Young,s modulus of elasticity Y is suspended form the roof of a building. A block of mass m is attached at lower end of the wire. If the block is displaced from its mean position and released then the block starts oscillating. Time period of these oscillations will be

View SolutionA cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that lon would execute SHM with a time period. T=2π√mApg where, m is mass of the body and p is density of the liquid.
View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hρρ1g
View Solution
