Choose the correct option:
Water is filled in a cylindrical container to a height of . The ratio of the cross-sectional area of the orifice and the beaker is . The square of the speed of the liquid coming out from the orifice is .

(a)
(b)
(c)
(d)
The correct Answer is:A
Applying continuity equation at 1 and 2, we have
...(i)
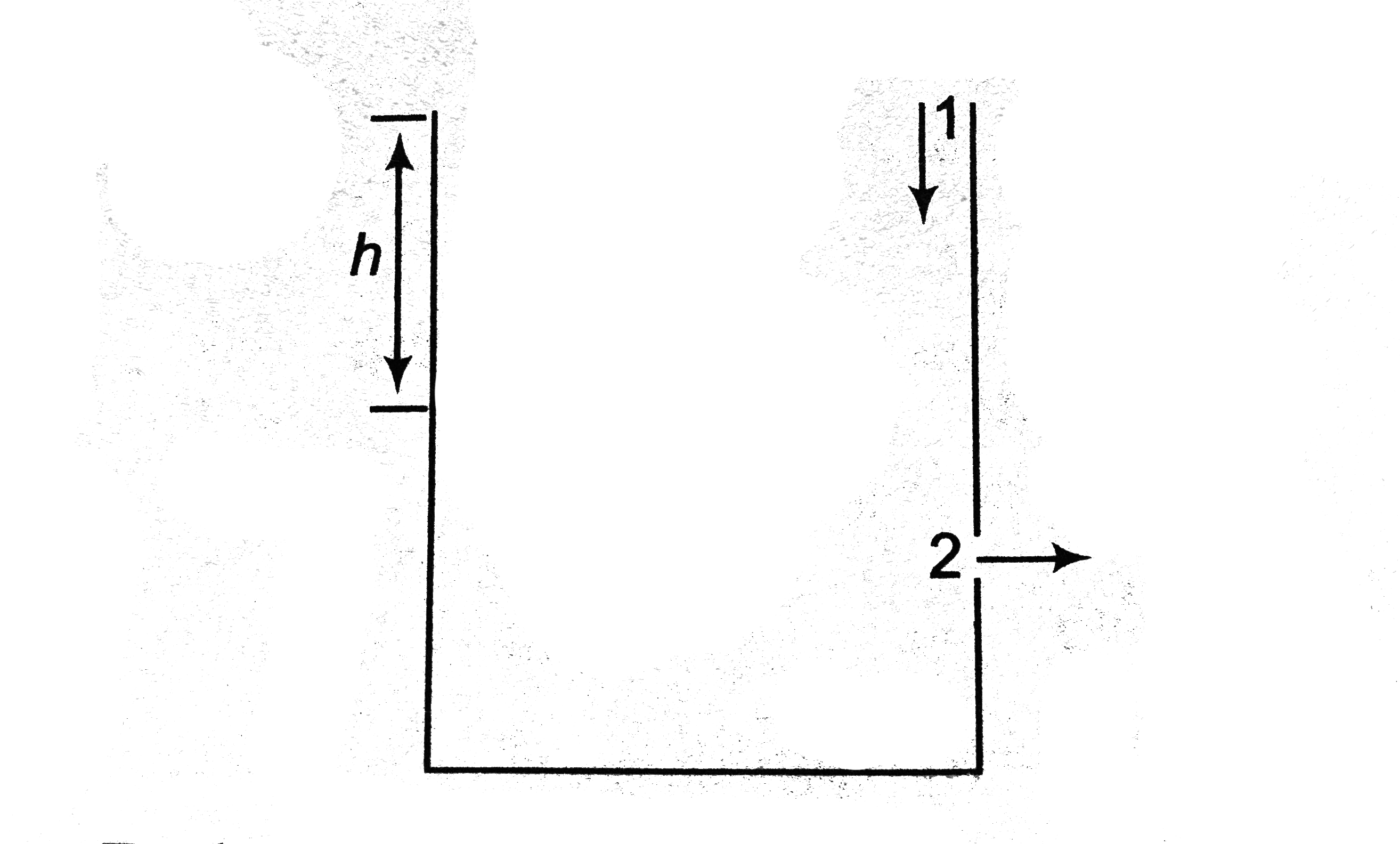
Further applying Bernoulli's equation at these two points, we have
...(ii)
Solving Eqs. (i) and (ii), we have
Substituting the values, we have
.
Topper's Solved these Questions
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Exercise16.6
Explore 4 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Exercise16.7
Explore 4 Videos
- FLUID MECHANICSBook:DC PANDEY ENGLISHChapter:FLUID MECHANICSExercise:Exercise16.4
Explore 4 Videos
- EXPERIMENTSBook:DC PANDEY ENGLISHChapter:EXPERIMENTSExercise:Subjective
Explore 15 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
Similar Questions
A liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionWater is filled in a container upto height 3m. A small hole of area 'a' is punched in the wall of the container at a height 52.5 cm from the bottom. The cross sectional area of the container is A. If a/A=0.1 then v2 is (where v is the velocity of water coming out of the hole)
View Solution
Knowledge Check
A cylindrical vessel of height 500mm has an orifice (small hole) at its bottom. The orifice is initially closed and water is filled in it up to height H. Now the top is completely sealed with a cap and the orifice at the bottom is opened. Some water comes out from the orifice and the water level in the vessel becomes steady with height of water column being 200mm. Find the fall in height(in mm) of water level due to opening of the orifice.
[Take atmospheric pressure =1.0×105N/m2, density of water=1000kg//m^3andg=10m//s^2. Neglect any effect of surface tension.]A6B4C2D8
A cylindrical vessel is filled with water upto a height of 1m. The cross-sectional area of the orifice at the bottom is (1/400) that of the vessel.
(a) What is the time required to empty the tank through the orifice at the bottom?
(b) What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of 1m from orifice?
View SolutionA horizontal pipeline carries water in a streamline flow. At a point along the tube where the cross sectional area is 10−2(m2), the water velcity is 2m/s and the pressure is 8000Pa. The pressure of water at another point where cross sectional area is 0.5×(10)−2(m2) is
View SolutionA tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
After long time, when the height of water inside the tank again becomes equal to H2, the solid cylinder is taken out. then the velocity of liquid flowing out of the orifice (just after removing the cylinder) will be
View SolutionA tank of square cross section (2m×2m) is filled with water up to a height of 2.5m. Find the thrust experienced by the vertical and botom of the tank (g=10m/s2).
View SolutionA tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
The speed of water flowing out of the orifice after the cylinder is kept inside it is
View SolutionA tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
The speed of water flowing out of the orifice after the cylinder is kept inside it is
View SolutionThe level of water in a tank is 5 m high. A hole of area of cross section 1 cm2 is made at the bottom of the tank. The rate of leakage of water for the hole in m3s−1 is (g=10ms−2)
View Solution