A block of ice of total area A and thicknes 0.5m is floating in water. In order to just support a man of nass 100kg, the area A should be (the specific gravity of ice is 0.9)
2.2m2
1.0m2
0.02m2
None of these
The correct Answer is:D
To solve the problem of determining the area A of the block of ice required to support a man of mass 100kg, we can follow these steps:
Step 1: Understand the Forces Acting on the Ice
When the ice block is floating, the weight of the man and the weight of the ice block must equal the buoyant force (upthrust) exerted by the water.
Step 2: Write the Equation for Equilibrium
The equilibrium condition can be expressed as:
Weight of the man+Weight of the ice=Buoyant force
Mathematically, this can be written as:
m1g+m2g=Vρwaterg
where:
- m1=100kg (mass of the man)
- m2 is the mass of the ice
- V is the volume of the displaced water (which is equal to the volume of the ice block submerged)
- ρwater=1000kg/m3 (density of water)
- g is the acceleration due to gravity (which will cancel out)
Step 3: Calculate the Mass of the Ice Block
The mass of the ice block can be calculated using its volume and density. The specific gravity of ice is given as 0.9, which means:
ρice=0.9×ρwater=0.9×1000kg/m3=900kg/m3
The volume V of the ice block can be expressed in terms of its area A and thickness t:
V=A×t
Given that the thickness t=0.5m, we can express the mass of the ice block as:
m2=Vρice=(A×0.5)×900
Step 4: Substitute and Rearrange the Equation
Substituting m2 into the equilibrium equation:
100kg⋅g+(A×0.5×900)⋅g=(A×0.5)×1000⋅g
Cancelling g from all terms:
100+450A=500A
Step 5: Solve for Area A
Rearranging the equation gives:
100=500A−450A
100=50A
A=10050=2m2
Conclusion
The area A required to just support the man is 2m2.
When the ice block is floating, the weight of the man and the weight of the ice block must equal the buoyant force (upthrust) exerted by the water.
The equilibrium condition can be expressed as:
Weight of the man+Weight of the ice=Buoyant force
Mathematically, this can be written as:
m1g+m2g=Vρwaterg
where:
- m1=100kg (mass of the man)
- m2 is the mass of the ice
- V is the volume of the displaced water (which is equal to the volume of the ice block submerged)
- ρwater=1000kg/m3 (density of water)
- g is the acceleration due to gravity (which will cancel out)
The mass of the ice block can be calculated using its volume and density. The specific gravity of ice is given as 0.9, which means:
ρice=0.9×ρwater=0.9×1000kg/m3=900kg/m3
The volume V of the ice block can be expressed in terms of its area A and thickness t:
V=A×t
Given that the thickness t=0.5m, we can express the mass of the ice block as:
m2=Vρice=(A×0.5)×900
Substituting m2 into the equilibrium equation:
100kg⋅g+(A×0.5×900)⋅g=(A×0.5)×1000⋅g
Cancelling g from all terms:
100+450A=500A
Rearranging the equation gives:
100=500A−450A
100=50A
A=10050=2m2
The area A required to just support the man is 2m2.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Level 1 Subjective
36 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Subjective Question
2 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Assertion and Reason
1 Video
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
An ice-cube of edge is 10 cm floating in water. Time period of small vertical oscillations of the cube is: (Specific gravity of ice is 0.9)
View SolutionA cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water? specific gravity of ice=0.9.
View SolutionA cubical block of ice floating in water has to suport metal piece weighing 0.5 kg. What can be the minimum edge of the block so that it does not sink in water/ specific gravity of ice=0.9.
View SolutionA solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
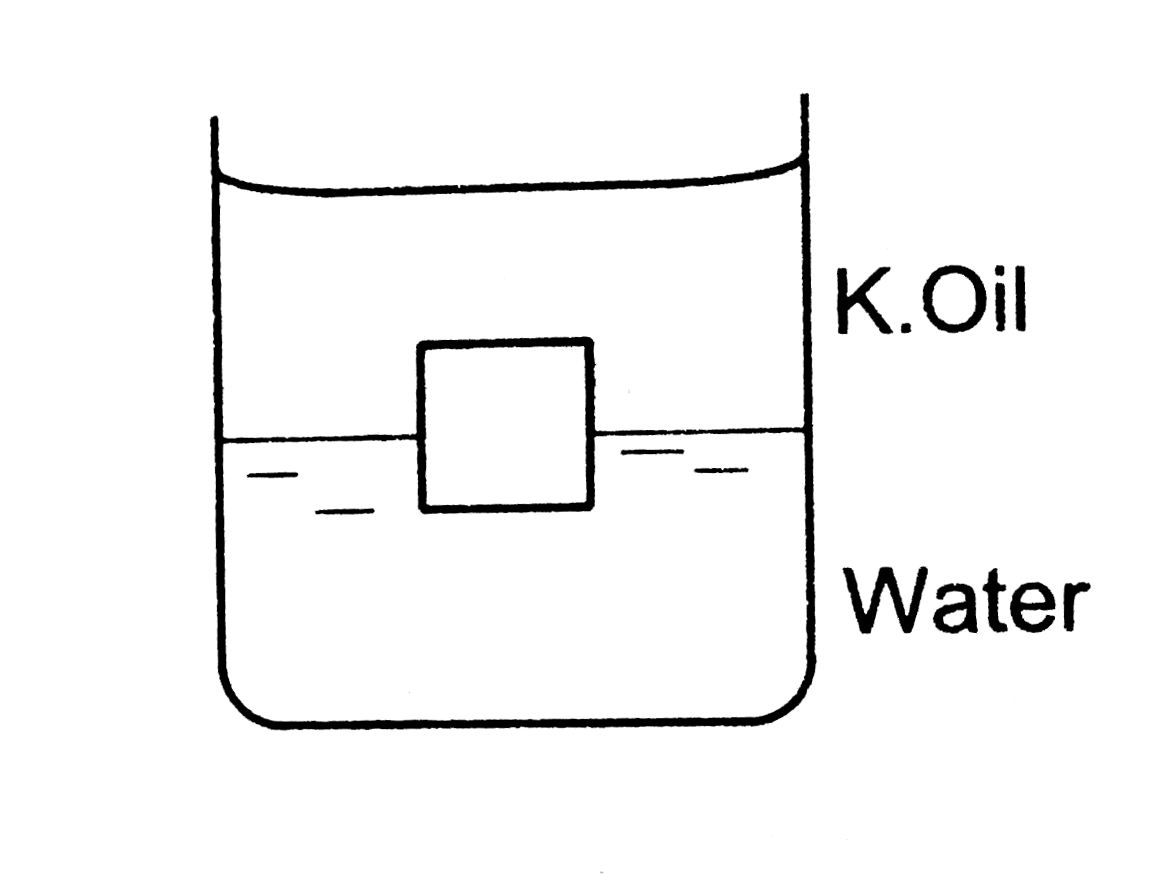
View SolutionA cube of ice floats partly in water and partly in K.oil figure. Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 and that of ice is 0.9.
View SolutionThe ratio of masses of a cubical block of wood and a chunk of concrete is 3/5 so that the combination just floats with entire volume submerged under water. If the specific gravity of wood is 0.5 then specific gravity of concrete will be
View SolutionA metal piece weighing 15g is heated to 100∘C and then immersed in a mixture of ice and water at the thermal equilibrium. The volume of the mixture is found to be reduced by 0.15cm3 with the temperature of mixture remaining constant. Find the specific heat of the metal. Given specific gravity of ice =0.92, specific gravity of water at 0∘C=1.0, latent heat of fusion of ice =80cal−g−1.
View SolutionA slab of stone of area of 0.36m2 and thickness 0.1m is exposed on the lower surface to steam at 100∘C. A block of ice at 0∘C rests on the upper surface of the slab. In one hour 4.8kg of ice is melted. The thermal conductivity of slab is
(Given latent heat of fusion of ice =3.63×105Jkg−1)
View SolutionA metal ball of specific gravity 4.5 and specific heat 0.1cal/gm−∘C is placed on a large slab of ice at 0∘C. Half of the ball sinks in the ice. The initial temperature of the ball is:- (Latent heat capacity of ice =80cal/g, specific gravity of ice =0.9)
View SolutionA block of ice with a lead shot embedded in it is floating on water contained in a vessel. The temperature of the system is maintained at 0∘C as the ice melts. When the ice melts completely the level of water in the vessel rises.
View Solution
