A hot body placed in air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being k times the temperature difference from the surrounding. Starting from t=0 , find the time in which the body will lose half the maximum heat it can lose.
The correct Answer is:B
To solve the problem of finding the time in which a hot body loses half the maximum heat it can lose according to Newton's law of cooling, we can follow these steps:
Step 1: Understand Newton's Law of Cooling
According to Newton's law of cooling, the rate of change of temperature of a body is proportional to the difference between its temperature and the ambient temperature. Mathematically, this can be expressed as:
dTdt=−k(T−T0)
where:
- T is the temperature of the body at time t,
- T0 is the ambient temperature,
- k is a positive constant.
Step 2: Set Up the Initial Conditions
Let T1 be the initial temperature of the body at t=0. Therefore, we have:
- At t=0, T=T1.
Step 3: Integrate the Equation
We can separate variables and integrate:
∫TT1dTT−T0=−k∫t0dt
This gives us:
ln|T−T0|∣∣∣TT1=−kt
Step 4: Solve the Integration
After integrating, we can express this as:
ln|T−T0|−ln|T1−T0|=−kt
This simplifies to:
ln(T−T0T1−T0)=−kt
Step 5: Exponentiate to Remove the Logarithm
Exponentiating both sides gives:
T−T0T1−T0=e−kt
Rearranging this, we find:
T=T0+(T1−T0)e−kt
Step 6: Determine the Maximum Heat Loss
The maximum heat loss Q that the body can lose is given by:
Q=mc(T1−T0)
To find the time when the body loses half of this maximum heat, we need to find when the temperature decreases by half of the maximum temperature difference:
ΔT=Q2=mc(T1−T0)2
Step 7: Set Up the Equation for Half Heat Loss
The temperature at which half the maximum heat is lost can be expressed as:
T=T0+(T1−T0)2
Step 8: Substitute and Solve for Time
Substituting this value of T into our equation from Step 5:
T0+(T1−T0)2−T0T1−T0=e−kt
This simplifies to:
(T1−T0)/2T1−T0=e−kt
Thus:
12=e−kt
Taking the natural logarithm of both sides gives:
ln(12)=−kt
Step 9: Solve for Time t
Rearranging this gives:
t=−ln(1/2)k=ln(2)k
Final Answer
The time in which the body will lose half the maximum heat it can lose is:
t=ln(2)k
According to Newton's law of cooling, the rate of change of temperature of a body is proportional to the difference between its temperature and the ambient temperature. Mathematically, this can be expressed as:
- T is the temperature of the body at time t,
- T0 is the ambient temperature,
- k is a positive constant.
Let T1 be the initial temperature of the body at t=0. Therefore, we have:
- At t=0, T=T1.
We can separate variables and integrate:
After integrating, we can express this as:
Exponentiating both sides gives:
The maximum heat loss Q that the body can lose is given by:
The temperature at which half the maximum heat is lost can be expressed as:
Substituting this value of T into our equation from Step 5:
Rearranging this gives:
The time in which the body will lose half the maximum heat it can lose is:
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 More Than One Correct
5 Videos
- BASIC MATHEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
Derive Newton's law of cooling to show that the rate of loss of heat from the body is proportional to the temperature difference between the body and its surroundings.
View SolutionAccording to Newton’s law of cooling, the rate of cooling of a body is proportional to (Δθ)n , where Δθis the difference of the temperature of the body and the surrounding, and n is equal to :
View Solution
Knowledge Check
A hot liquid is kept in a bog room. Accoding to Newton's law of cooling rate of cooling liquid (represented as y) is plotted against its temperature T. Which of the following curves may represent the plot?
A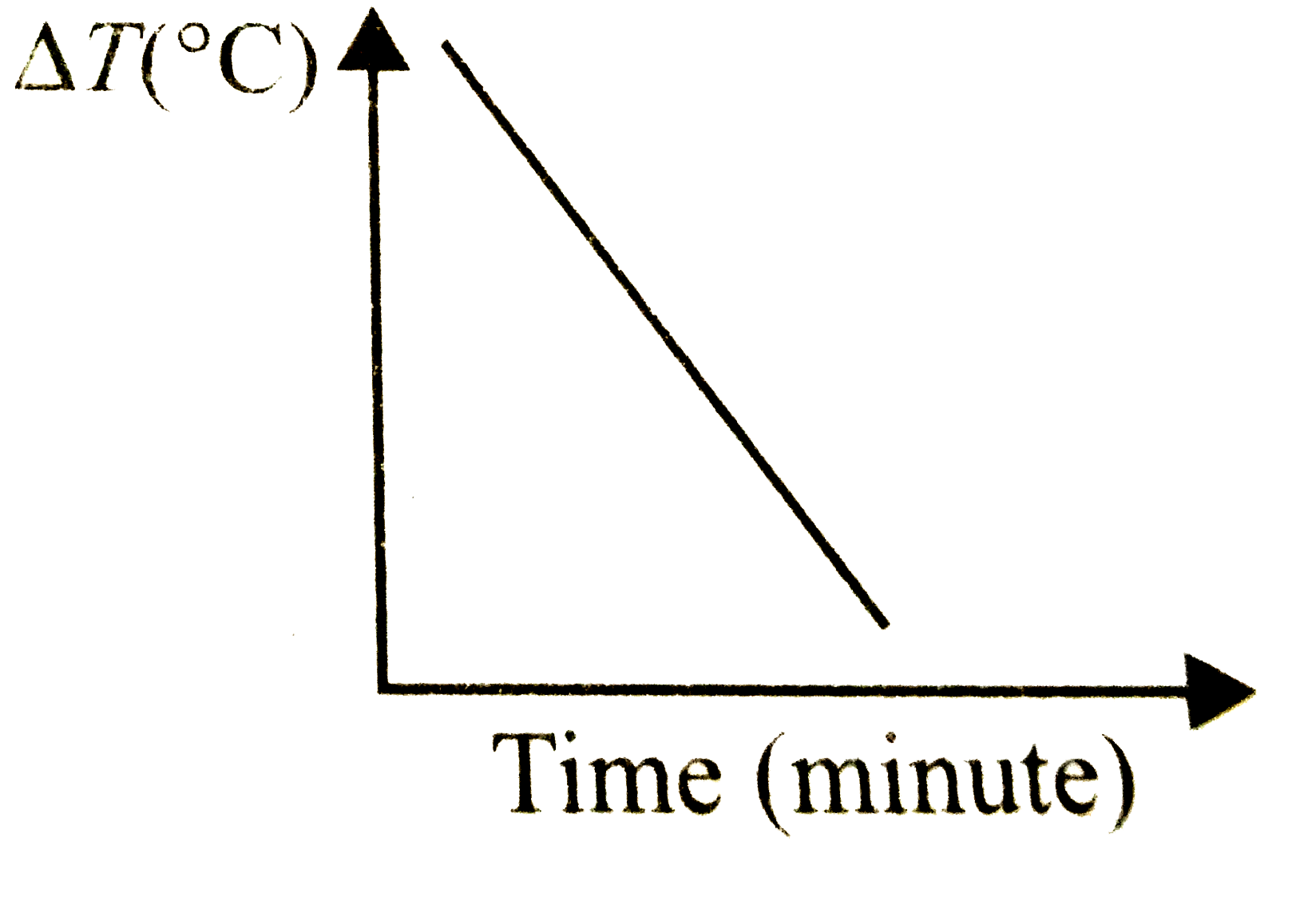 B
B C
C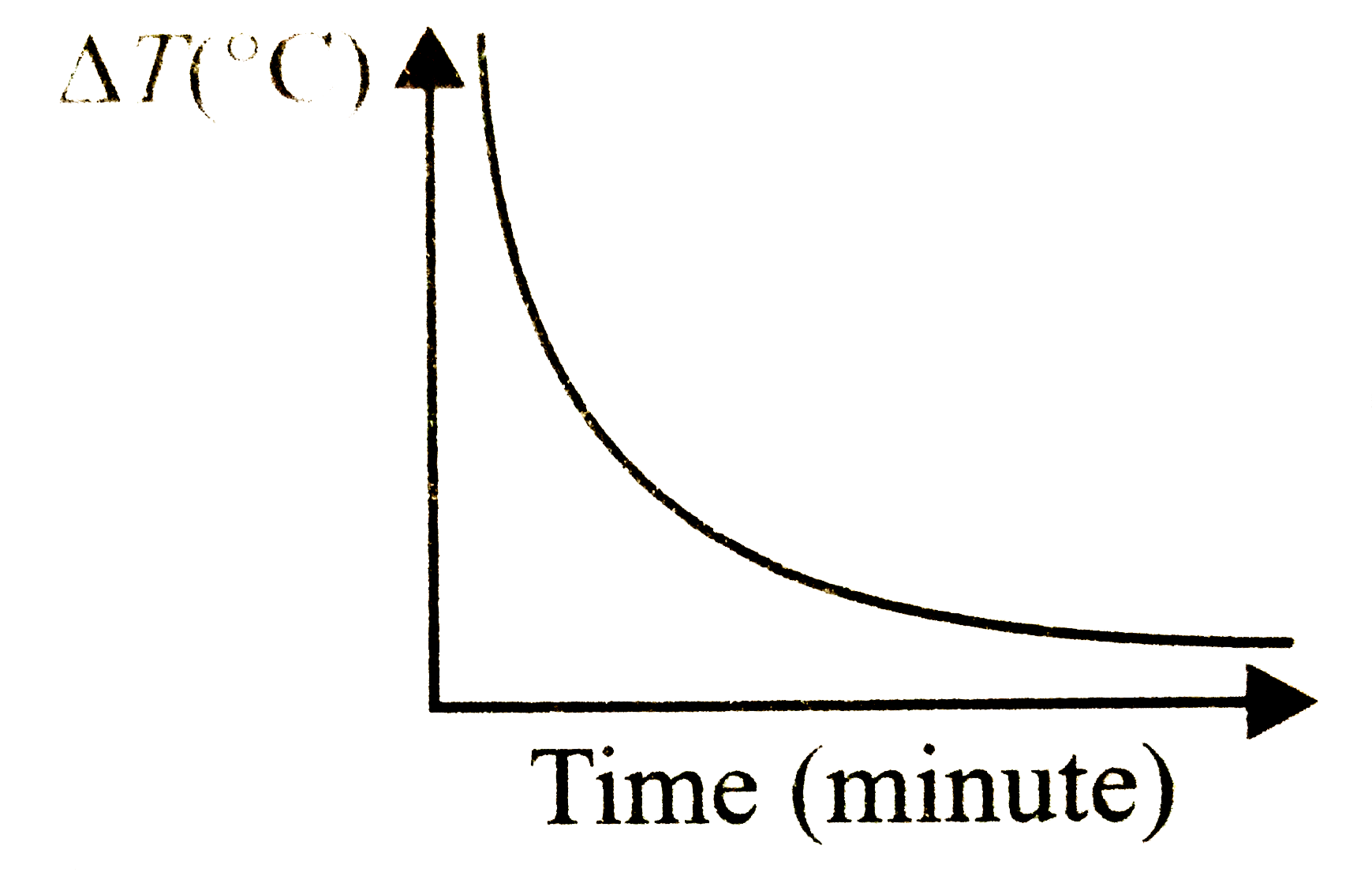 D
D
Assertion: According to Newton's law of cooling, the rate of loss of heat, −dQ/dt of the body is directly proportional to the difference of temperature.
Reason :This law holds for all type of temperature differences.Alaw of thermometryBNewton's law of coolingClaw of calorimetryDzeroth law
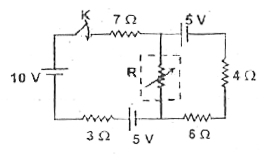
In the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
View SolutionA hot liquid is kept in a big room. According to Newton's law of cooling rate of cooling liquid (represented as y) is plotted against its temperature T. Which of the following curves may represent the plot?
View SolutionA hot body placed in a surrounding of temperature θ0 obeys Newton's law of cooling dθdt=−k(θ−θ0) . Its temperature at t=0 is θ1 the specific heat capacity of the body is s and its mass is m. Find
(a) the maximum heat that the body can lose and
(b) the time starting from t=0 in which it will lose 90% of this maximum heat.
View SolutionIf the system were lossing heat according to Newton's cooling law the temperature of the mixture would change with time according to (while heater was on) .
View SolutionA liquid in a beaker has temperature θ(t) at time t and θ0 is temperature of surroundings, then according to Newton's law of cooling the correct graph between loge(θ−θ0) and t is :
View SolutionA body at a temperature of 500F is placed outdoors where the temperature is 1000F . If the rate of change of the temperature of a body is proportional to the temperature difference between the body and its surrounding medium. If after 5 min the temperature of the body is 600F , find (a) how long it will take the body to reach a temperature of 750 F and (b) the temperature of the body after 20 min.
View Solution
