Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
√r1r2
r1+r2
r1−r2
r1+r22
The correct Answer is:C
To solve the problem, we need to analyze the circuit with two cells connected in series, each having the same electromotive force (emf) and different internal resistances. We will derive the value of the external resistance R based on the given conditions.
1. Understanding the Circuit:
- We have two cells connected in series with the same emf E.
- The internal resistances of the cells are r1 and r2 respectively, where r1>r2.
- The external resistance is denoted as R.
2. Condition Given:
- It is stated that the potential difference across the first cell (with internal resistance r1) is zero when the circuit is closed. This means that the entire voltage drop across this cell is equal to its internal resistance drop.
3. Applying Kirchhoff's Law:
- According to Kirchhoff's loop rule, the sum of potential differences in a closed loop must equal zero. For our circuit, we can express this as:
E−I⋅r1−I⋅r2−I⋅R=0
- Rearranging gives:
E=I⋅(r1+r2+R)
4. Finding the Current:
- Since the potential difference across the first cell is zero, we can write:
E−I⋅r1=0⟹I=Er1
5. Substituting Current in the Equation:
- Now substitute I back into the equation derived from Kirchhoff's law:
E=Er1⋅(r1+r2+R)
6. Simplifying the Equation:
- Dividing both sides by E (assuming E≠0):
1=(r1+r2+R)r1
- Rearranging gives:
r1=r1+r2+R
7. Solving for R:
- Rearranging the equation further:
R=r1−r2
Final Answer:
The value of the external resistance R is:
R=r1−r2
- We have two cells connected in series with the same emf E.
- The internal resistances of the cells are r1 and r2 respectively, where r1>r2.
- The external resistance is denoted as R.
- It is stated that the potential difference across the first cell (with internal resistance r1) is zero when the circuit is closed. This means that the entire voltage drop across this cell is equal to its internal resistance drop.
- According to Kirchhoff's loop rule, the sum of potential differences in a closed loop must equal zero. For our circuit, we can express this as:
E−I⋅r1−I⋅r2−I⋅R=0
- Rearranging gives:
E=I⋅(r1+r2+R)
- Since the potential difference across the first cell is zero, we can write:
E−I⋅r1=0⟹I=Er1
- Now substitute I back into the equation derived from Kirchhoff's law:
E=Er1⋅(r1+r2+R)
- Dividing both sides by E (assuming E≠0):
1=(r1+r2+R)r1
- Rearranging gives:
r1=r1+r2+R
- Rearranging the equation further:
R=r1−r2
The value of the external resistance R is:
R=r1−r2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Two sources of equal emf are connected to an external resistance R. The internal resistance of the two sources areR1andR2(R1>R1). If the potential difference across the source having internal resistance R2 is zero, then
View SolutionTwo cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
View Solution
Knowledge Check
A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A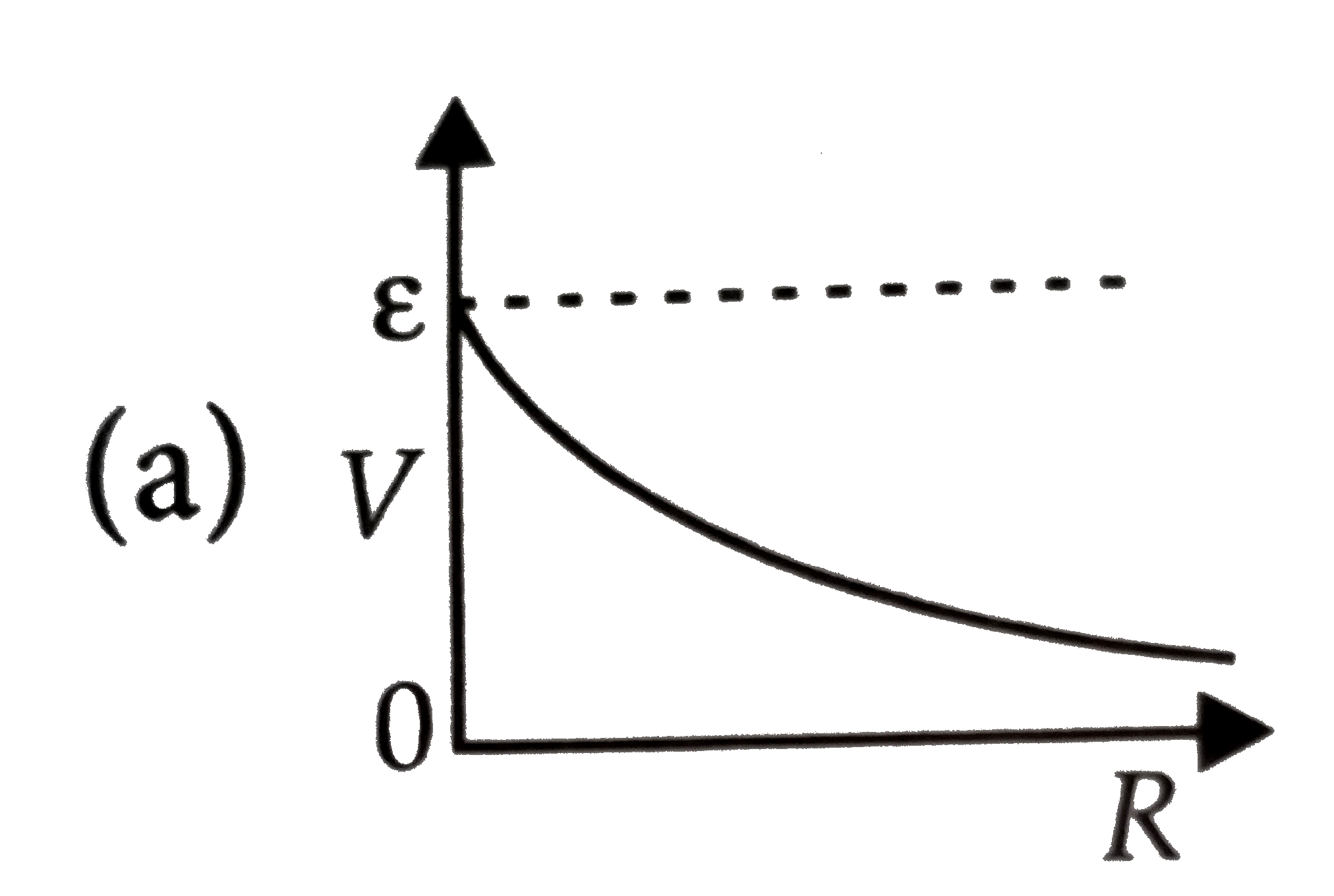 B
B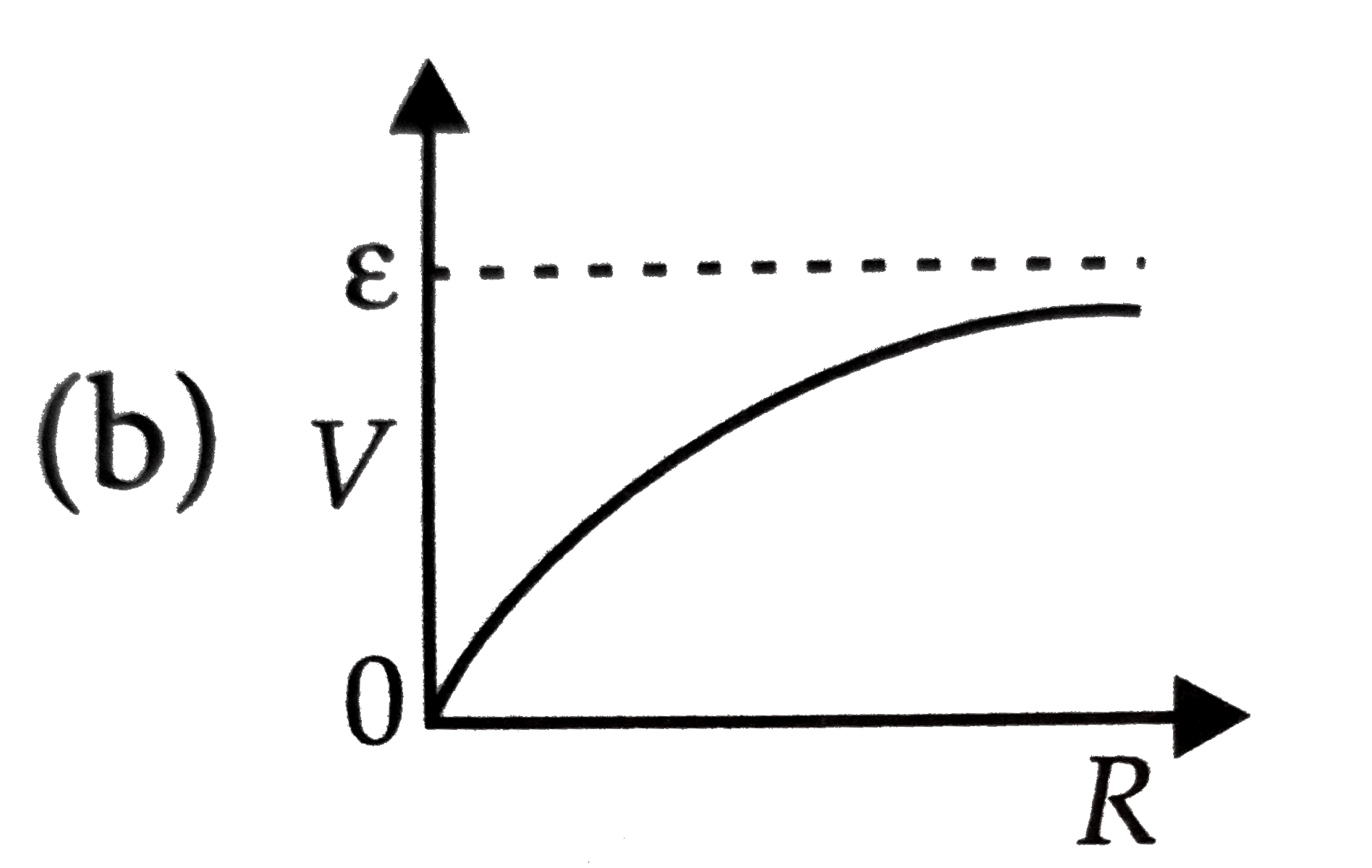 C
C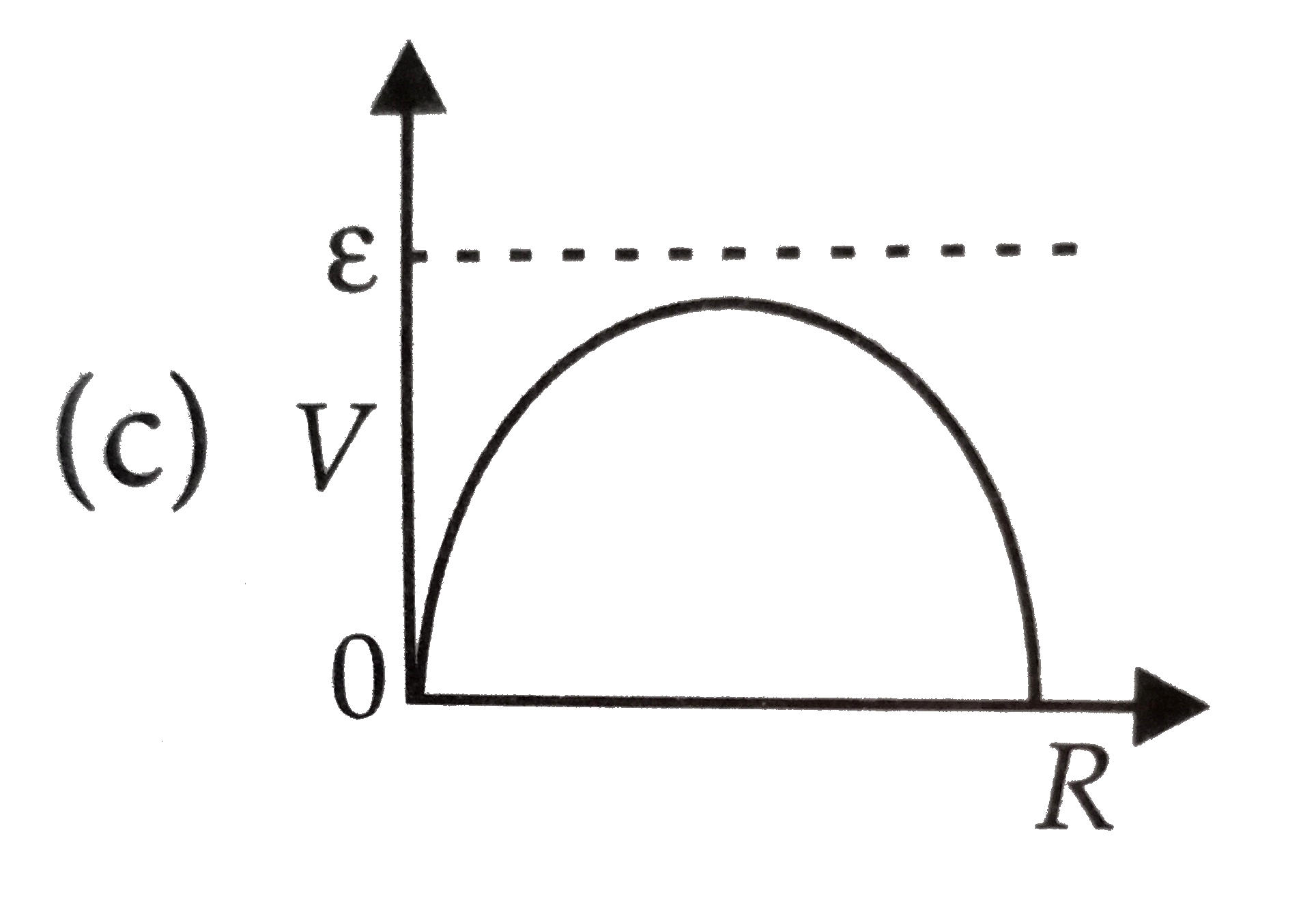 D
D
Two cells of emf E each and internal resistance r1 and r2 are connected in series across a load resistance R. If potential difference across the first cell is zero, then find the relation between R,r1 and r2
View SolutionTwo sources of equal emf are connected in series and having different internal resistance r1 and r2(r2>r1). Find the external resistance R at which the potential difference across the terminals of one of the sources becomes equal to zero.
View SolutionAccording to this diagram , the potential difference across the terminals is ( internal resistance of cell =r)
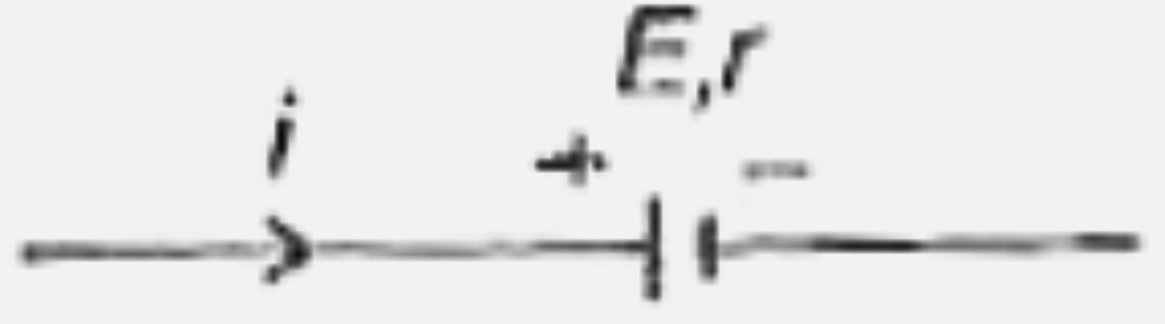
View SolutionTwo cells of the same e.mf. e but different internal resistances r1andr2 are connected in series with an external resistance 'R'. The potential drop across the first cell is found to be zero. The external resistance Ris

View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance R. By mistake one of the cells is connected in reverse. Then, the current in the external circuit is
View SolutionIn the given circuit the cells have zero internal resistance. The currents (in Amperes) passing through resistance R1andR2 respectively, are :
View SolutionA cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View Solution
