If E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
The correct Answer is:C
To solve the problem, we need to find the potential difference (V) across the external resistance (R) in a circuit that includes a cell with an electromotive force (E) and an internal resistance (r).
1. Understanding the Circuit:
- We have a cell with an EMF (E) and an internal resistance (r).
- The external resistance is denoted as (R).
- The circuit can be represented as a series circuit where the internal resistance (r) and the external resistance (R) are connected in series.
2. Applying Ohm's Law:
- The total resistance (R_total) in the circuit is the sum of internal resistance and external resistance:
Rtotal=r+R
3. Calculating Current (I):
- According to Ohm's Law, the current (I) flowing through the circuit can be calculated using the formula:
I=ERtotal=Er+R
4. Finding the Potential Difference (V) across External Resistance (R):
- The potential difference (V) across the external resistance (R) can be calculated using Ohm's law:
V=I⋅R
- Substituting the expression for current (I) we found earlier:
V=(Er+R)⋅R
- Therefore, we can express the potential difference across the external resistance (R) as:
V=E⋅Rr+R
Final Answer:
The potential difference across the external resistance (R) is given by:
V=E⋅Rr+R
---
- We have a cell with an EMF (E) and an internal resistance (r).
- The external resistance is denoted as (R).
- The circuit can be represented as a series circuit where the internal resistance (r) and the external resistance (R) are connected in series.
- The total resistance (R_total) in the circuit is the sum of internal resistance and external resistance:
Rtotal=r+R
- According to Ohm's Law, the current (I) flowing through the circuit can be calculated using the formula:
I=ERtotal=Er+R
- The potential difference (V) across the external resistance (R) can be calculated using Ohm's law:
V=I⋅R
- Substituting the expression for current (I) we found earlier:
V=(Er+R)⋅R
- Therefore, we can express the potential difference across the external resistance (R) as:
V=E⋅Rr+R
The potential difference across the external resistance (R) is given by:
V=E⋅Rr+R
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
A cell of e.m.f E and internal resitance r ,is connected to an external resistance R. the variation of potential difference V across the resistance R as function of R as shown in the figure, is the best represented by curve
_PHY_E01_011_Q01.png)
View Solution2A cell having an emf ε and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
View Solution
Knowledge Check
A cell having an emf E and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by
A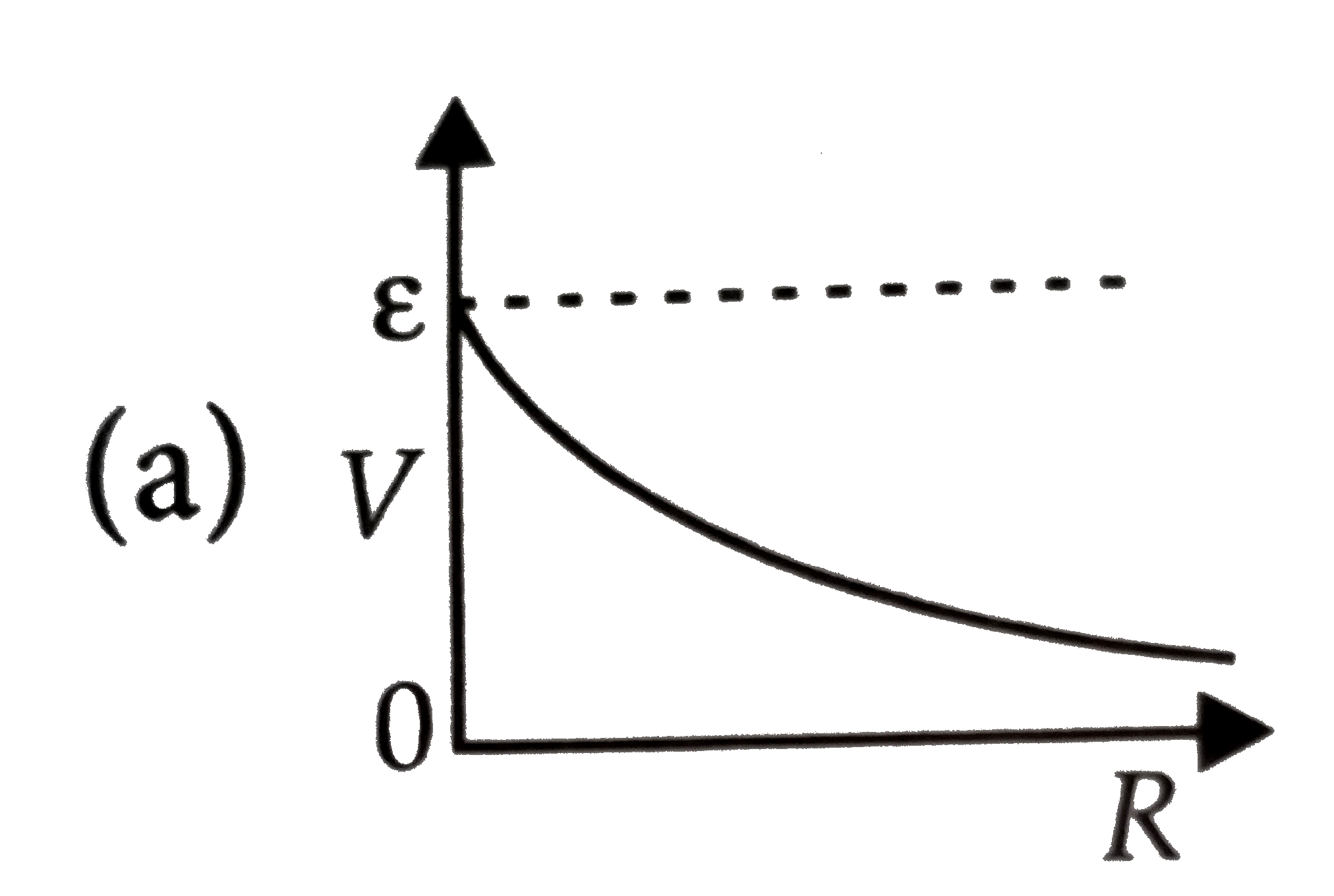 B
B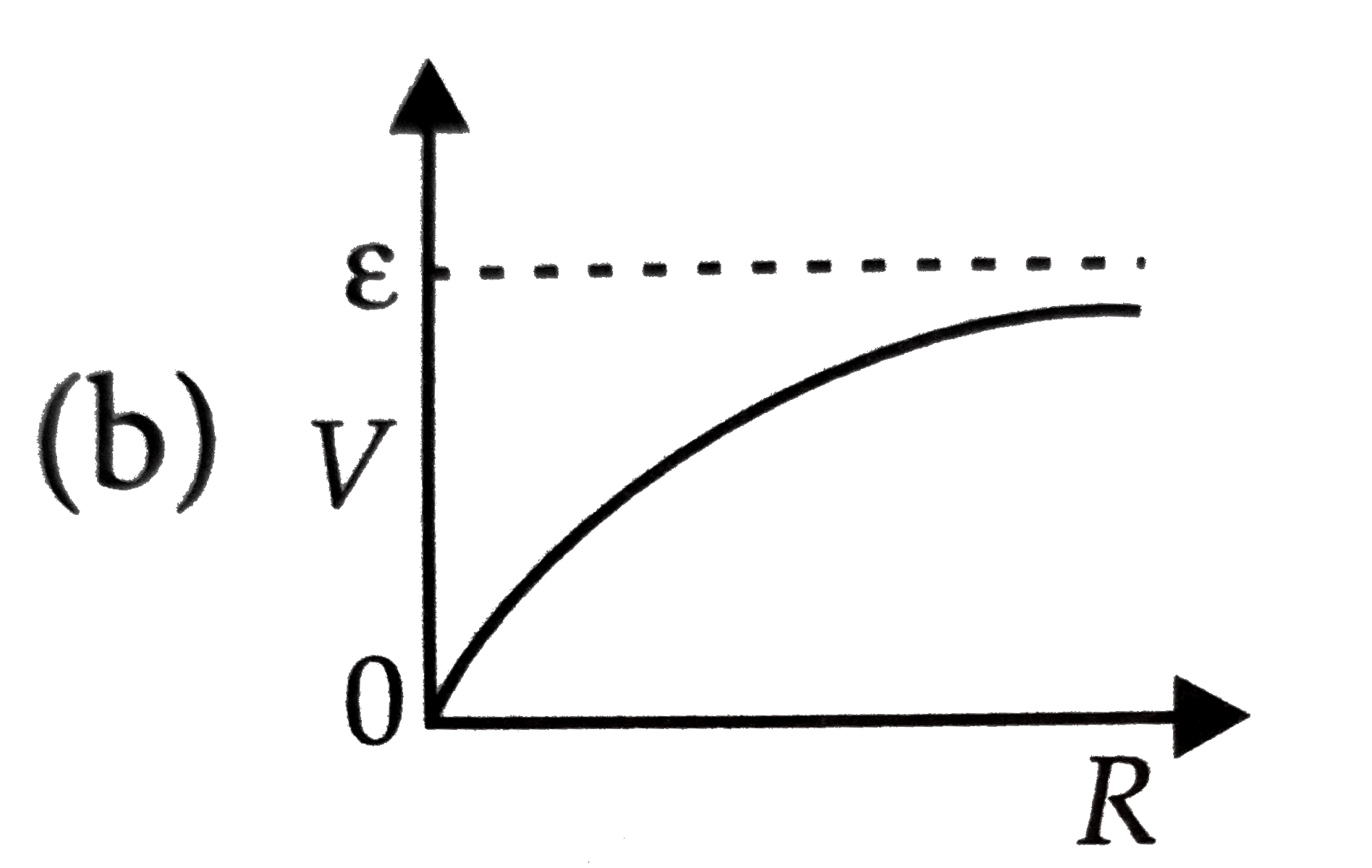 C
C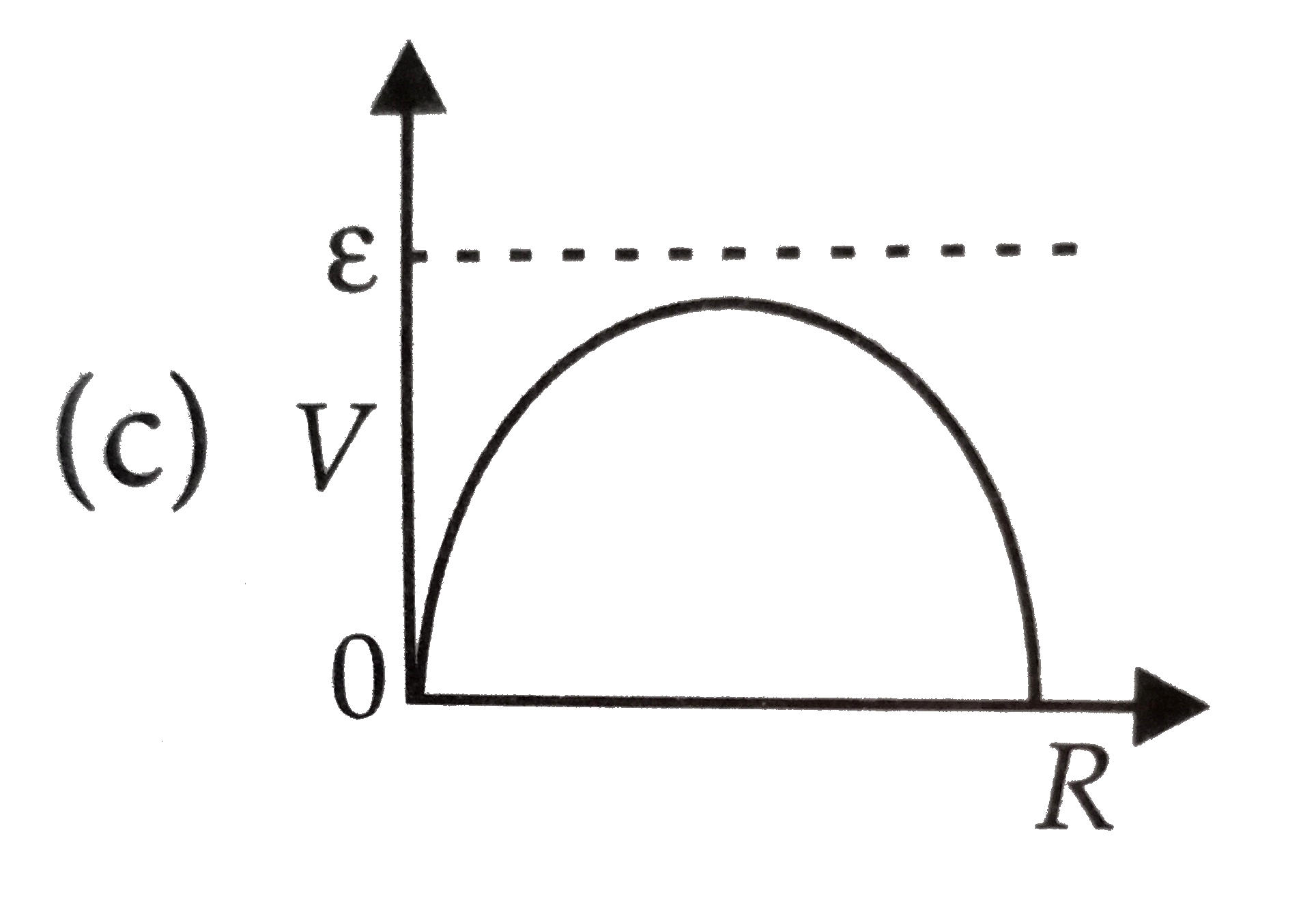 D
D
A capacitor is conneted to a cell emf E having some internal resistance r. The potential difference across the
View SolutionTwo sources of equal emf are connected in series and having different internal resistance r1 and r2(r2>r1). Find the external resistance R at which the potential difference across the terminals of one of the sources becomes equal to zero.
View SolutionA resistor R is connected to a cell of emf e and internal resistance r. Potential difference across the resistor R is found to be V. State the relation between e, V, R and r.
View SolutionA cell which has an emf 1.5 V is connectedin series with an external resistance of 10Ω. If the potential difference across the cell is 1.25 V, then the internal resistance of the cell is (inΩ)
View SolutionA voltmeter of resistance 994Ω is connected across a cell of emf 1 V and internal resistance 6Ω. Find the potential difference across the voltmeter, that across the terminals of the cell and percantage error in the reading of the voltmeter.
View SolutionA cell of e.m. E and internal resistance r is connected across a resistancer. The potential difference between the terminals of the cell must be
View SolutionThe emf of a cell is ε and its internal resistance is r. its termnals are cannected to a resistance R. The potential difference between the terminals is 1.6V for R = 4 Omega, and 1.8 V for R = 9 Omega. Then,
View Solution
