The current in a circuit with an external resistance of 3.75Ωis2.5A. When a resistance of 1Ω is introduced into the circuit, the current becomes 0.4A. The emf of the power source is
1V
2V
3V
4V
The correct Answer is:B
To find the EMF of the power source in the given circuit, we can follow these steps:
Step 1: Write down the initial conditions and equations
We are given:
- External resistance R=3.75Ω
- Current I1=2.5A
Using Ohm's law, we can express the EMF E in terms of the internal resistance r:
I1=ER+r
Substituting the known values:
2.5=E3.75+r(Equation 1)
Step 2: Write down the conditions after adding a resistance
When a resistance of 1Ω is added:
- New total resistance R′=3.75+1=4.75Ω
- New current I2=0.4A
Using Ohm's law again:
I2=ER′+r⟹0.4=E4.75+r(Equation 2)
Step 3: Solve Equation 1 for E
From Equation 1:
E=2.5(3.75+r)
Expanding this gives:
E=9.375+2.5r(Equation 3)
Step 4: Solve Equation 2 for E
From Equation 2:
E=0.4(4.75+r)
Expanding this gives:
E=1.9+0.4r(Equation 4)
Step 5: Set Equations 3 and 4 equal to each other
Since both equations represent E, we can set them equal:
9.375+2.5r=1.9+0.4r
Step 6: Solve for r
Rearranging gives:
9.375−1.9=0.4r−2.5r
7.475=−2.1r
r=−7.4752.1≈−3.55Ω
Step 7: Substitute r back into either equation to find E
Using Equation 3:
E=9.375+2.5(−3.55)
Calculating this gives:
E=9.375−8.875=0.5V
Final Answer
The EMF of the power source is approximately:
E≈0.5V
We are given:
- External resistance R=3.75Ω
- Current I1=2.5A
I1=ER+r
Substituting the known values:
2.5=E3.75+r(Equation 1)
When a resistance of 1Ω is added:
- New total resistance R′=3.75+1=4.75Ω
- New current I2=0.4A
I2=ER′+r⟹0.4=E4.75+r(Equation 2)
From Equation 1:
E=2.5(3.75+r)
Expanding this gives:
E=9.375+2.5r(Equation 3)
From Equation 2:
E=0.4(4.75+r)
Expanding this gives:
E=1.9+0.4r(Equation 4)
Since both equations represent E, we can set them equal:
9.375+2.5r=1.9+0.4r
Rearranging gives:
9.375−1.9=0.4r−2.5r
7.475=−2.1r
r=−7.4752.1≈−3.55Ω
Using Equation 3:
E=9.375+2.5(−3.55)
Calculating this gives:
E=9.375−8.875=0.5V
The EMF of the power source is approximately:
E≈0.5V
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - OBJECTIVE_TYPE
1 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 Subjective
53 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 1 Assertion And Reason
11 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
the current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View SolutionIn the circuit shown, the current in 3Ω resistance is

View SolutionThe figure shows a source (a battery) with an emf E of 12 V with an internal resistance r of 2Ω and an external resistance of 4Ω is added to complete the circuit. What are the voltmeter and ammeter readings
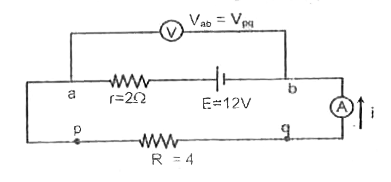
View SolutionThe current in a simple series cirucit is 5A. When an additional resistance of 2Ω is introduced, the current is reduced to 4A. Calculate the resistance of the original circuit. Assume that the applied potential difference is the same in both the cases.
View SolutionThe circuit shown in the figure contains two diodes each with a forward resistance of 50Ω and with infinite backward resistance. If the batter of 6 V is connected in the circuit, then the current through the 100Ω resistance is
View SolutionFind the current in each resistor of the circuit shown in fig
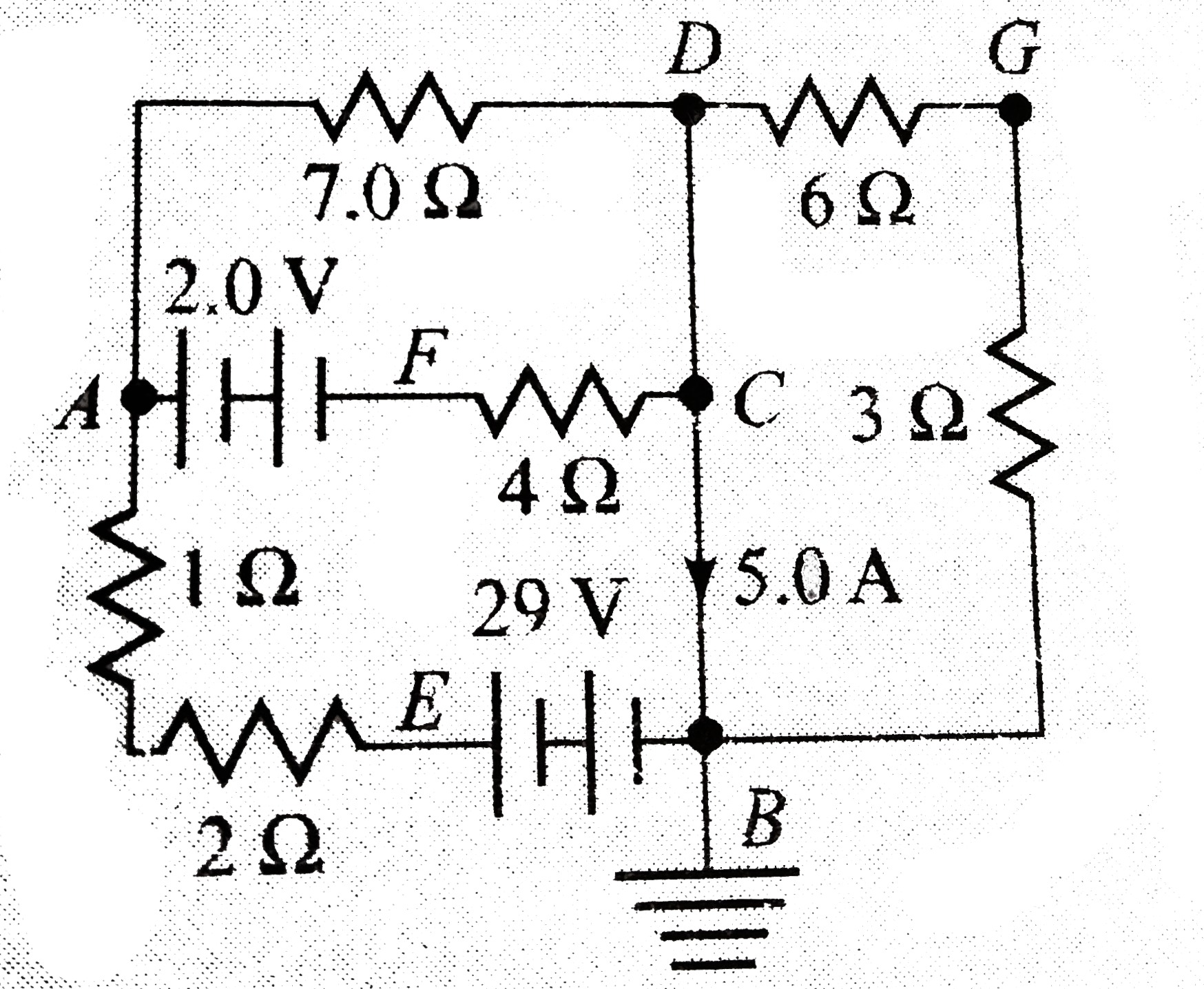
a. Current thorugh resistance of 6Ωis………..
b. Current thorugh resistance of 3Ωis………..
c. Current thorugh resistance of 2Ωis………..
d. Current thorugh resistance of 5Ωis………..
View SolutionIn a series LCR circuit, the total reactance is 4Ω and resistance is 3Ω . Its power factor is
View SolutionCurrent in 3Ω resistance is

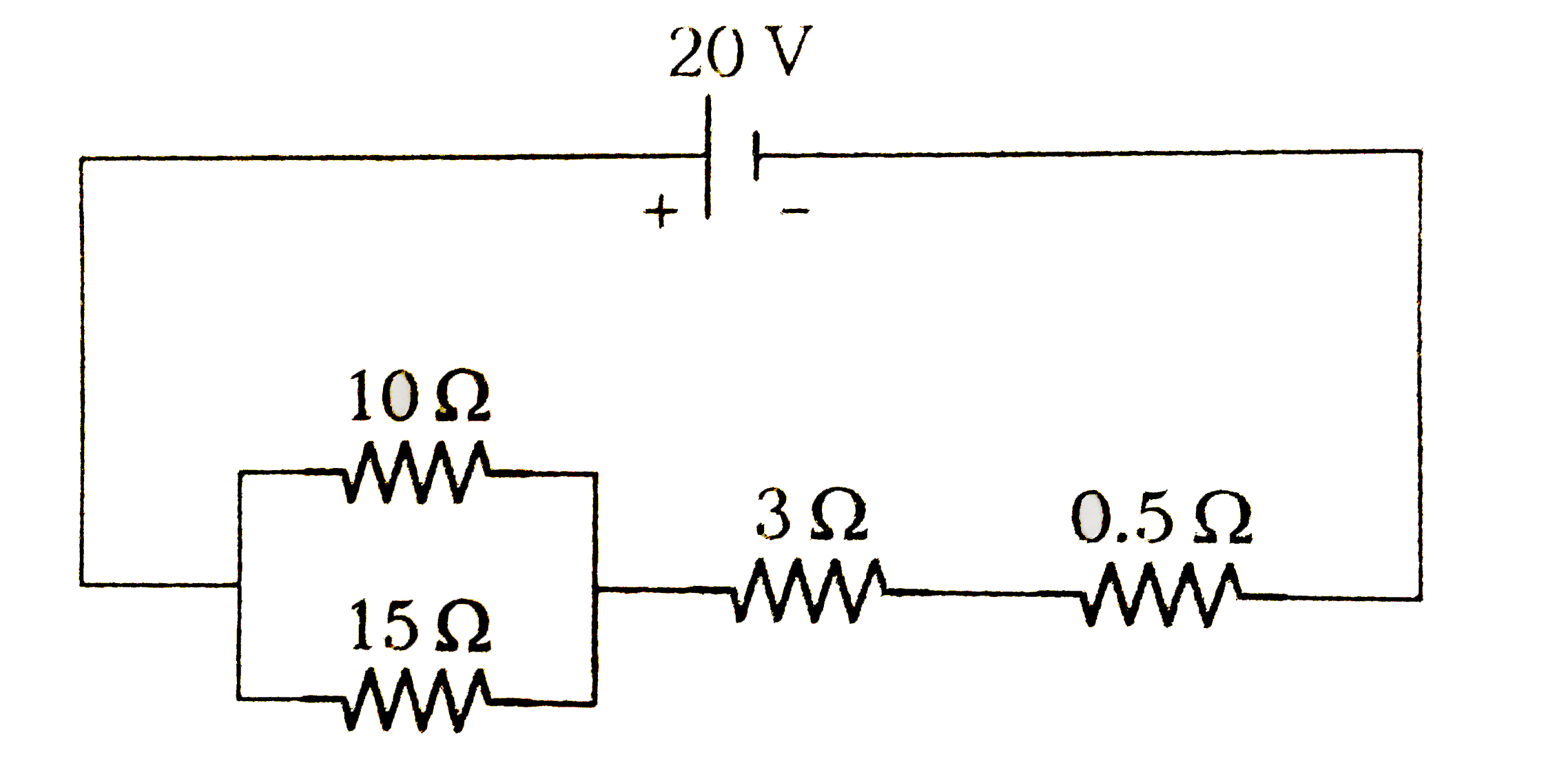
View SolutionIn the circuit, the current flowing through 10Ω resistance is
View Solution
