An ammeter with resistance RA is connected in series with a resistor R, a battery of emf c and internal resistance r. The current measured by the ammeter is IA. Find the current through the circuit if the ammeter is removed so that the battery and the resistor form a complete circuit. Express your answer in terms of IA,r,RA and R. Show that more "ideal" the ammeter, the smaller the difference between this current and the current IA. ltbr> (b) If R=3.80Ω,ε=7.50V and r=0.45Ω, find the maximum value of the ammeter resistance RA so that IA is within 99% of the current in the circuit when the ammeter is absent. (c) Explain why your answer in part (b) represents a maximum value.
The correct Answer is:A, B, D
To solve the problem step by step, we will break it down into parts as per the question.
Part (a): Finding the current through the circuit when the ammeter is removed
1. Understanding the Circuit with the Ammeter:
When the ammeter (with resistance RA) is connected in series with the resistor R and the battery (with EMF ϵ and internal resistance r), the total resistance in the circuit is R+RA+r.
The current measured by the ammeter, IA, can be expressed as:
IA=ϵR+RA+r
2. Finding the EMF:
Rearranging the equation for ϵ:
ϵ=IA×(R+RA+r)(1)
3. Removing the Ammeter:
When the ammeter is removed, the circuit now consists only of the battery and the resistor R. The current in this case, denoted as I′A, can be expressed as:
I′A=ϵR+r
4. Substituting for EMF:
Substitute the expression for ϵ from equation (1) into the equation for I′A:
I′A=IA×(R+RA+r)R+r
5. Simplifying the Expression:
This can be simplified as:
I′A=IA×R+RA+rR+r
6. Final Expression:
Thus, the current through the circuit when the ammeter is removed can be expressed as:
I′A=IA×(1+RAR+r)
Part (b): Finding the maximum value of the ammeter resistance RA
1. Condition for 99% of Current:
We need to find RA such that IA is within 99% of I′A:
IA=0.99I′A
2. Substituting for I′A:
Substitute the expression for I′A:
IA=0.99×IA×(1+RAR+r)
3. Rearranging the Equation:
Dividing both sides by IA (assuming IA≠0):
1=0.99(1+RAR+r)
10.99=1+RAR+r
10.99−1=RAR+r
4. Calculating RA:
RA=(R+r)(10.99−1)
5. Substituting Values:
Given R=3.80Ω, ϵ=7.50V, and r=0.45Ω:
R+r=3.80+0.45=4.25Ω
RA=4.25(10.99−1)≈4.25×(1.0101−1)≈4.25×0.0101≈0.0429Ω
Part (c): Explanation of Maximum Value
The value of RA calculated represents a maximum value because if RA were to increase beyond this point, the current IA would drop below 99% of I′A. This is due to the fact that as RA increases, the total resistance in the circuit increases, thereby reducing the current IA measured by the ammeter. Hence, the condition IA=0.99I′A would no longer hold.
When the ammeter (with resistance RA) is connected in series with the resistor R and the battery (with EMF ϵ and internal resistance r), the total resistance in the circuit is R+RA+r.
The current measured by the ammeter, IA, can be expressed as:
IA=ϵR+RA+r
Rearranging the equation for ϵ:
ϵ=IA×(R+RA+r)(1)
When the ammeter is removed, the circuit now consists only of the battery and the resistor R. The current in this case, denoted as I′A, can be expressed as:
I′A=ϵR+r
Substitute the expression for ϵ from equation (1) into the equation for I′A:
I′A=IA×(R+RA+r)R+r
This can be simplified as:
I′A=IA×R+RA+rR+r
Thus, the current through the circuit when the ammeter is removed can be expressed as:
I′A=IA×(1+RAR+r)
We need to find RA such that IA is within 99% of I′A:
IA=0.99I′A
Substitute the expression for I′A:
IA=0.99×IA×(1+RAR+r)
Dividing both sides by IA (assuming IA≠0):
1=0.99(1+RAR+r)
10.99=1+RAR+r
10.99−1=RAR+r
RA=(R+r)(10.99−1)
Given R=3.80Ω, ϵ=7.50V, and r=0.45Ω:
R+r=3.80+0.45=4.25Ω
RA=4.25(10.99−1)≈4.25×(1.0101−1)≈4.25×0.0101≈0.0429Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Level 2 Single Correct
Explore 26 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Level 2 More Than One Correct
Explore 10 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:OBJECTIVE_TYPE
Explore 1 Video
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrances gallery
Explore 25 Videos
Similar Questions
Find the current measured by the ammeter in the circuit shown in figure

View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of 10Ω through an ammeter of resistance 2Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View Solution
Knowledge Check
A battery of emf 15 V and internal resistance of 4Ω is connected to a resistor. If the current in the circuit is 2A and the circuit is closed. Resistance of the resistor and terminal voltage of the battery will be
A2.5Ω,6VB3.5Ω,6VC2.5Ω,7VD3.5Ω,7V
In the circuit shown below, E is a battery of emf 6 V and internal resistance 1Ω. Find the reading of the ammeter A. if it has negligible resistance :
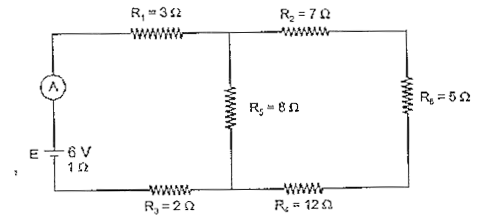
View SolutionA set of 'n' equal resistor, of value of 'R' each are connected in series to a battery of emf 'E' and internal resistance 'R'. The current drawn is I. Now, the 'n' resistors are connected in parallel to the same battery. Then the current drawn from battery becomes 10.1. The value of 'n' is
View SolutionAn ammeter and a voltmeter are connected in series to an ideal battery of emf E. If the ammeter reads I and voltmeter reading V, then
View SolutionA resistor R is conneted to a parallel combination of two identical batteries each with emf E and an internal resistance r. The potential drop across the resistance R is.
View Solution(A) : An ammeter is connected in series in the circuit.
(R) : An ammeter is a high resistance galvanometer.
View SolutionFirst a set of n equal resistors of R each are connected in series to a battery of emf E and internal resistance R. A current I is observed to flow. Then, the n resistors are connected in parallel to the same battery. It is observed that the current is increased 10 times. What is 'n'?
View SolutionAn ammeter and a voltmeter of resistance R connected in seires to an electric cell of negligible internal resistance. Their readings are A and V respecitvely. If another resistance R is connected in parallel with the voltmeter
View Solution