A resistor R is conneted to a parallel combination of two identical batteries each with emf E and an internal resistance r. The potential drop across the resistance R is.
2ER2R+r
ER2R+r
ER2R+r
2ERR+2r
The correct Answer is:A
To solve the problem, we need to find the potential drop across the resistor R when it is connected to a parallel combination of two identical batteries, each with an EMF E and an internal resistance r.
1. Identify the Circuit Configuration:
We have two identical batteries connected in parallel, each with an EMF E and an internal resistance r. The external resistor R is connected across this parallel combination.
2. Calculate the Equivalent EMF:
In a parallel circuit, the EMF remains the same as that of one battery. Therefore, the equivalent EMF Eeq of the two batteries is:
Eeq=E
3. Calculate the Equivalent Internal Resistance:
The internal resistances of the two batteries in parallel can be calculated using the formula for resistances in parallel:
1req=1r+1r=2r
Thus, the equivalent internal resistance req is:
req=r2
4. Simplify the Circuit:
Now, we can simplify the circuit to a single battery with EMF E and an internal resistance r2 connected to the external resistor R.
5. Calculate the Total Resistance:
The total resistance in the circuit is the sum of the equivalent internal resistance and the external resistance:
Rtotal=R+req=R+r2
6. Calculate the Total Current:
Using Ohm's law, the total current I flowing through the circuit can be calculated as:
I=ER+r2
7. Calculate the Potential Drop Across the Resistor R:
The potential drop VR across the resistor R can be calculated using Ohm's law:
VR=I⋅R=(ER+r2)⋅R
8. Final Expression for the Potential Drop:
Substituting the expression for I gives:
VR=E⋅RR+r2
Final Answer:
The potential drop across the resistance R is:
VR=E⋅RR+r2
We have two identical batteries connected in parallel, each with an EMF E and an internal resistance r. The external resistor R is connected across this parallel combination.
In a parallel circuit, the EMF remains the same as that of one battery. Therefore, the equivalent EMF Eeq of the two batteries is:
Eeq=E
The internal resistances of the two batteries in parallel can be calculated using the formula for resistances in parallel:
1req=1r+1r=2r
Thus, the equivalent internal resistance req is:
req=r2
Now, we can simplify the circuit to a single battery with EMF E and an internal resistance r2 connected to the external resistor R.
The total resistance in the circuit is the sum of the equivalent internal resistance and the external resistance:
Rtotal=R+req=R+r2
Using Ohm's law, the total current I flowing through the circuit can be calculated as:
I=ER+r2
The potential drop VR across the resistor R can be calculated using Ohm's law:
VR=I⋅R=(ER+r2)⋅R
Substituting the expression for I gives:
VR=E⋅RR+r2
The potential drop across the resistance R is:
VR=E⋅RR+r2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-2)
16 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-3)
22 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-3)
2 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Videos
Similar Questions
A capacitor is conneted to a cell emf E having some internal resistance r. The potential difference across the
View SolutionFind the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure

View Solution
Knowledge Check
Three resistances 2Ω,4Ω,5Ω are combined in series and this combination is connected to a battery of 12 V emf and negligible internal resistance. The potential drop across these resistances are
A(5,45,4.36,2.18)VB(2,18,5.45,4.36)VC(4.36,2.18,5.45)VD(2.18,4.36,5.45)V
(a) Three resistors 1Ω,2Ω and 3Ω are combined in series. What is the total resistance of the combination ?
(b) If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
View SolutionFind the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure

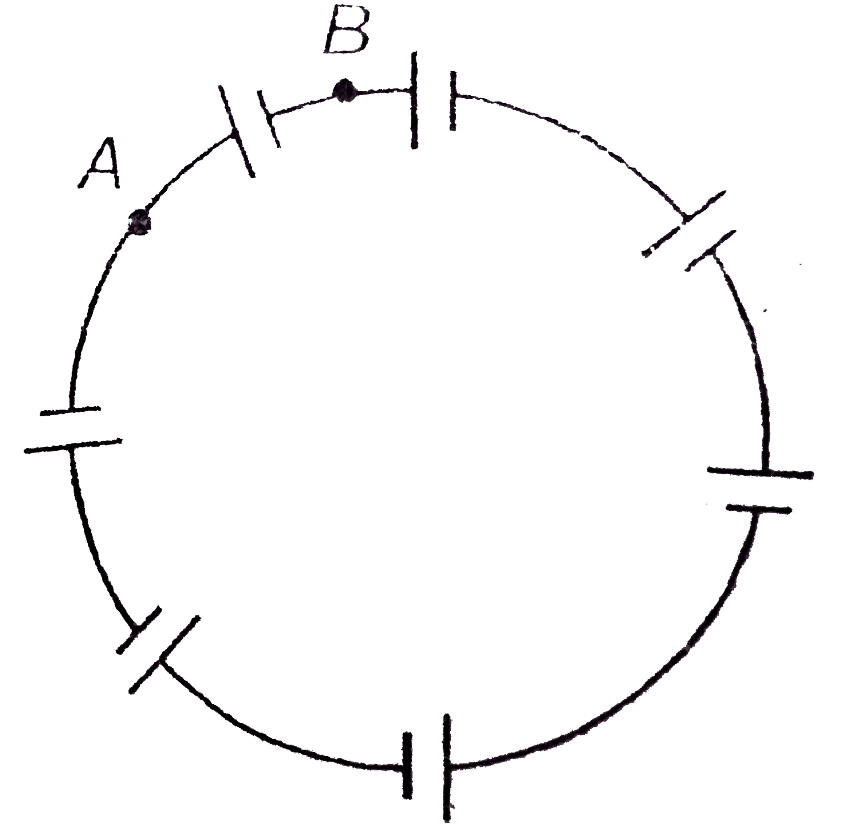
View SolutionSeven identical cells each of e.m.f. E and internal resistance r are connected as shown . The potential difference between A and B is
View SolutionA resistor R is connected to a cell of emf e and internal resistance r. Potential difference across the resistor R is found to be V. State the relation between e, V, R and r.
View SolutionThe series combination of two batteries, both of the same emf 20 V, but different internal resistance of 10 Ω and 2 Ω , is connected to the parallel combination of two resistors 10 ohm and RΩ . The voltage difference across the battery of internal resistance 10Ω is zero, the value of R(∈Ω) is _________.
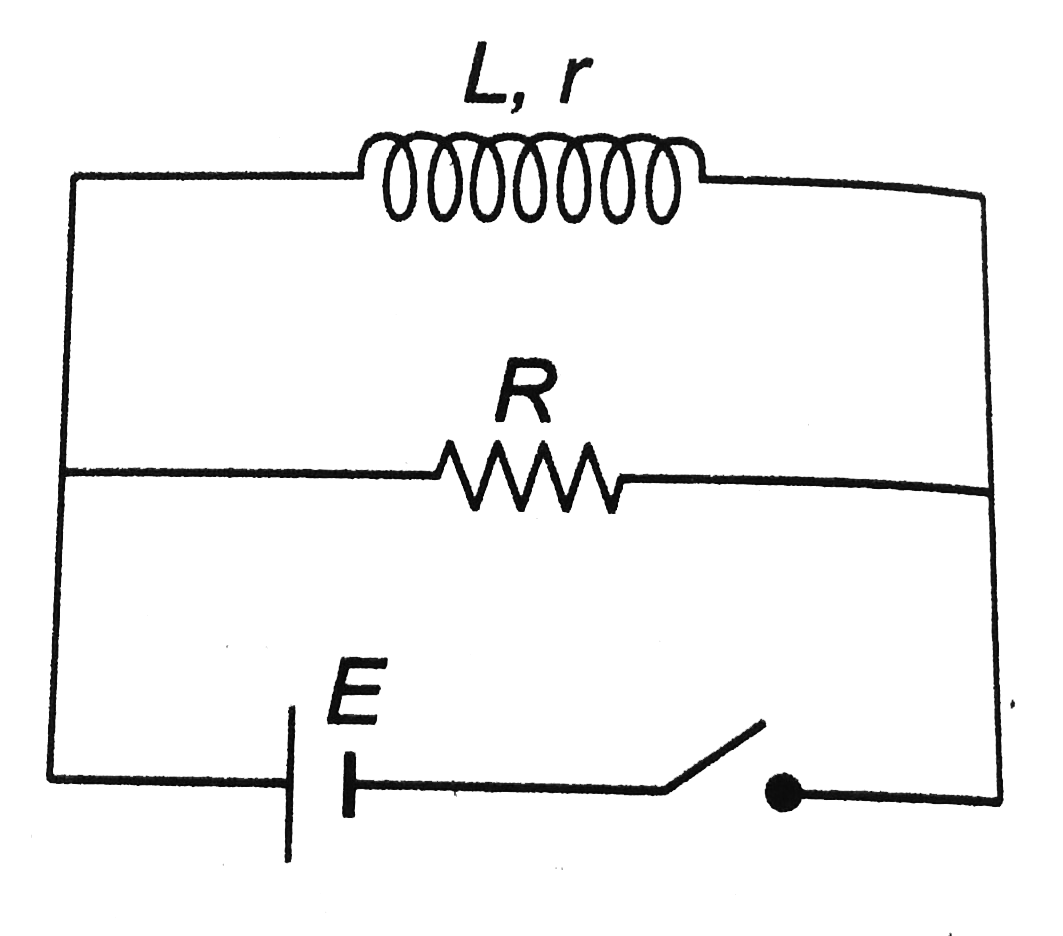
View SolutionA solenoid of inductance L with resistance r is connected in parallel to a resistance R. A battery of emf E and of negligible internal resistance is connected across the parallel combination as shown in the figure. At time t=0, switch S is opened, calculate
(a) current through the solenoid after the switch is opened.
(b) amount of heat generated in the solenoid.
View SolutionA capacitor of capacitance 1μF is connected in parallel with a resistance 10Ω and the combination is connected across the terminals of a battery of EMF 50 V and internal resistance 1Ω. The potential difference across the capacitor at steady state is (in Volt)
View Solution
