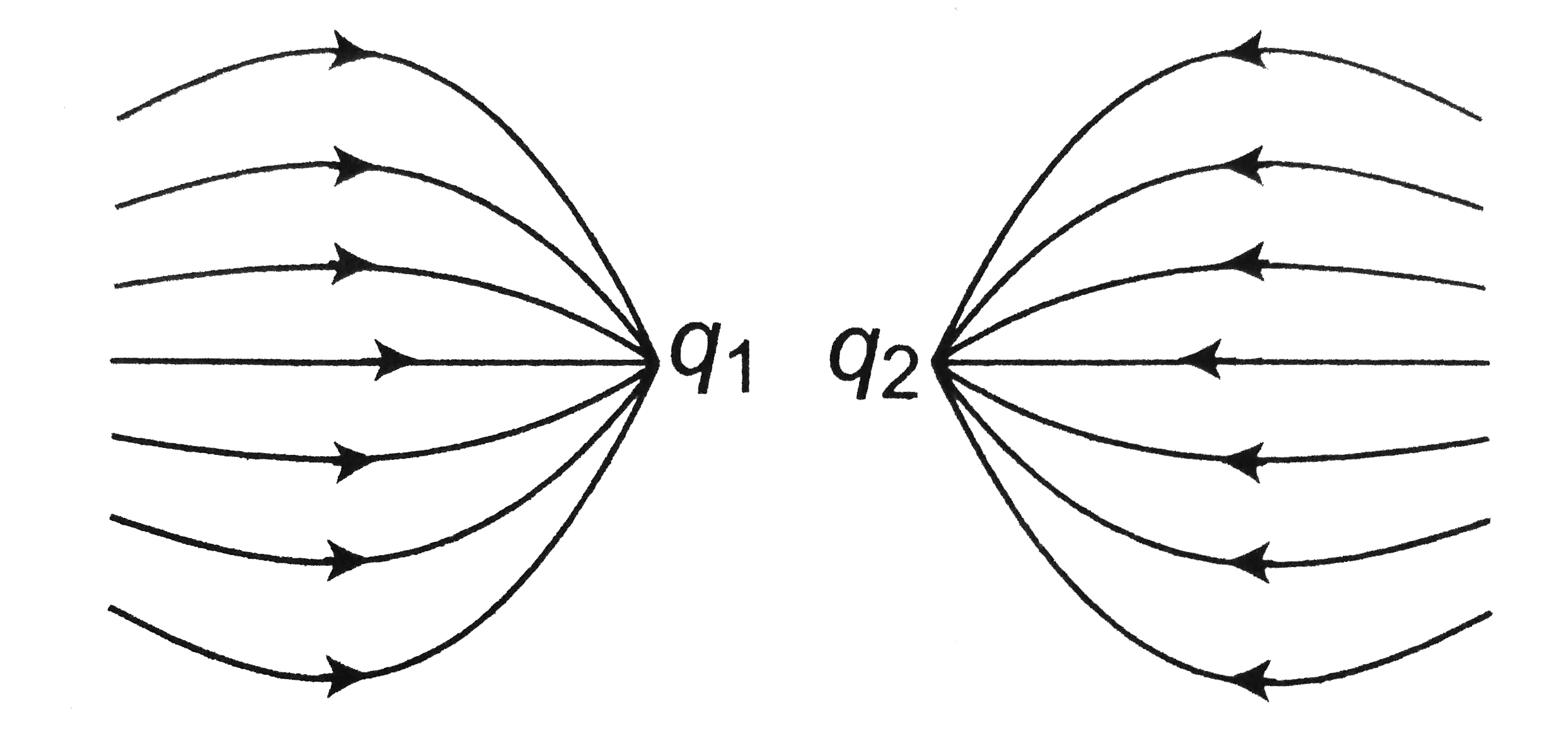
Draw electric lines of forces due to an electic dipole.
To draw the electric lines of force due to an electric dipole, follow these steps:
Step 1: Understand the Concept of an Electric Dipole
An electric dipole consists of two equal and opposite charges, +q and -q, separated by a small distance d. The dipole moment (p) is given by the product of the charge and the distance between the charges:
p=q⋅d
Step 2: Draw the Charges
Begin by sketching two points representing the charges. Place the positive charge (+q) on the left and the negative charge (-q) on the right. Label the distance between them as d.
Step 3: Draw Electric Field Lines from Each Charge
- From the Positive Charge (+q): Draw lines radiating outward from the positive charge. These lines represent the electric field lines that emerge from the positive charge. The lines should be drawn straight and should spread out as they move away from the charge.
- Towards the Negative Charge (-q): Draw lines that terminate at the negative charge. These lines represent the electric field lines that are attracted to the negative charge.
Step 4: Indicate the Behavior of the Field Lines
- Closer to the Charges: Near the charges, the electric field lines should be drawn closely spaced, indicating a stronger electric field.
- Farther from the Charges: As you move away from the dipole, the lines should be spaced further apart, indicating a weaker electric field.
Step 5: Draw Lines in the Space Between the Charges
In the region between the two charges, draw lines that start from the positive charge and curve towards the negative charge. This shows the interaction between the two charges and how the field lines behave in the vicinity of the dipole.
Step 6: Draw Additional Lines
To complete the diagram, draw additional field lines that start from the positive charge and extend towards infinity, as well as lines that extend from infinity towards the negative charge. This indicates that the electric field exists in the entire space around the dipole.
Step 7: Label the Diagram
Finally, label the positive charge (+q), the negative charge (-q), and the distance d between them. You may also label the electric field lines to indicate their direction (from positive to negative).
Final Diagram
Your final diagram should show a clear representation of the electric field lines due to an electric dipole, illustrating how they emerge from the positive charge and terminate at the negative charge, with additional lines indicating the field extending to infinity.
---
An electric dipole consists of two equal and opposite charges, +q and -q, separated by a small distance d. The dipole moment (p) is given by the product of the charge and the distance between the charges:
p=q⋅d
Begin by sketching two points representing the charges. Place the positive charge (+q) on the left and the negative charge (-q) on the right. Label the distance between them as d.
- From the Positive Charge (+q): Draw lines radiating outward from the positive charge. These lines represent the electric field lines that emerge from the positive charge. The lines should be drawn straight and should spread out as they move away from the charge.
- Towards the Negative Charge (-q): Draw lines that terminate at the negative charge. These lines represent the electric field lines that are attracted to the negative charge.
- Closer to the Charges: Near the charges, the electric field lines should be drawn closely spaced, indicating a stronger electric field.
- Farther from the Charges: As you move away from the dipole, the lines should be spaced further apart, indicating a weaker electric field.
In the region between the two charges, draw lines that start from the positive charge and curve towards the negative charge. This shows the interaction between the two charges and how the field lines behave in the vicinity of the dipole.
To complete the diagram, draw additional field lines that start from the positive charge and extend towards infinity, as well as lines that extend from infinity towards the negative charge. This indicates that the electric field exists in the entire space around the dipole.
Finally, label the positive charge (+q), the negative charge (-q), and the distance d between them. You may also label the electric field lines to indicate their direction (from positive to negative).
Your final diagram should show a clear representation of the electric field lines due to an electric dipole, illustrating how they emerge from the positive charge and terminate at the negative charge, with additional lines indicating the field extending to infinity.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 64videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 83videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery37videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
Similar Questions
Electric Dipole
View SolutionThe electric field at a point due to an electric dipole, on an axis inclined at an angle θ(<90∘) to the dipole axis, is perpendicular to the dipole axis, if the angle θ is
View SolutionWhat is the angle between the directions of electric field due to an electric dipole and its dipole moment at any :
(i) Axial p oint . (ii) Equatorial point .View SolutionTwo lines of force due to a bar magnet
View Solution(a) Define electric dipole moment. Is it a scalar or a vector ? Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
(b) Draw the equipotential surfaces due to an electric dipole. Locate the points where the potential due to the dipole is zero.View SolutionFigure shows electric lines of forces due to charges Q1 and Q2 Henice
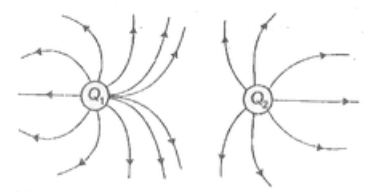
 View Solution
View Solution(A) : No two electric lines of force can intersect each other
(R ): Tangent at any point of electric line of force gives the direction of electric field.View Solution(A ): A charged particle free to move in an electric field always move along an electric line of force.
(R ): The electric line of force diverge from a positive charge and converge at a negative charge.View SolutionThe electrostatic potnetial due to an electric dipole at an equatorial point is
View SolutionFigure shows the electric field lines around an electric dipole. Which of the arrows best represents the electric field at point P ?
 View Solution
View Solution

