An infinite sheet of charge has surface charge density σ . The separation between two equipotential surfaces, whose potential differ by V is:
σV2∈0
2∈0Vσ
∈0Vσ
2σ∈0V
The correct Answer is:B
To solve the problem of finding the separation between two equipotential surfaces with a potential difference V due to an infinite sheet of charge with surface charge density σ, we can follow these steps:
1. Understand the Electric Field due to an Infinite Sheet of Charge:
The electric field E produced by an infinite sheet of charge with surface charge density σ is given by the formula:
E=σ2ϵ0
This electric field is uniform and acts perpendicular to the sheet.
2. Relate Electric Field to Potential Difference:
The relationship between electric field E, potential difference V, and separation D between two equipotential surfaces is given by:
V=E⋅D
Rearranging this equation gives us:
D=VE
3. Substitute the Expression for Electric Field:
Substitute the expression for E into the equation for D:
D=Vσ2ϵ0=V⋅2ϵ0σ
4. Final Expression for Separation:
Thus, the separation D between the two equipotential surfaces is:
D=2ϵ0Vσ
Conclusion:
The separation between the two equipotential surfaces whose potential differs by V is given by:
D=2ϵ0Vσ
The electric field E produced by an infinite sheet of charge with surface charge density σ is given by the formula:
E=σ2ϵ0
This electric field is uniform and acts perpendicular to the sheet.
The relationship between electric field E, potential difference V, and separation D between two equipotential surfaces is given by:
V=E⋅D
Rearranging this equation gives us:
D=VE
Substitute the expression for E into the equation for D:
D=Vσ2ϵ0=V⋅2ϵ0σ
Thus, the separation D between the two equipotential surfaces is:
D=2ϵ0Vσ
The separation between the two equipotential surfaces whose potential differs by V is given by:
D=2ϵ0Vσ
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 260videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN65videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 0 (LONG ANSWER TYPE )8videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE52videos
ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
Similar Questions
An infinite sheet of charge has a surfaces charge density of 10−7Cm2. The separation between two equipotential surfce whose potentials differ by 5V is
View SolutionAn infinite nonconducting sheet of charge has a surface charge density of 107C/m2. The separation between two equipotential surfaces near the whose potential differ by 5V is
View Solution
Knowledge Check
- Question 1 - Select One
An infinite cylinder of radius ro, carrying linear charge density λ. The equation of the equipotential surface for the cylinder is
Ar=r0eπε0[V(r)+V(r0)]λBr=r0e2πε0[V(r)−V(r0)]λ2Cr=r0e−2πε0[V(r)=V(r0)]λDr=r0e−2πε0[V(r)−V(r0)]λ
An infinite conducting sheet has surface charge density σ. The distance between two points is r. The potential difference (VA−VB) between these point is
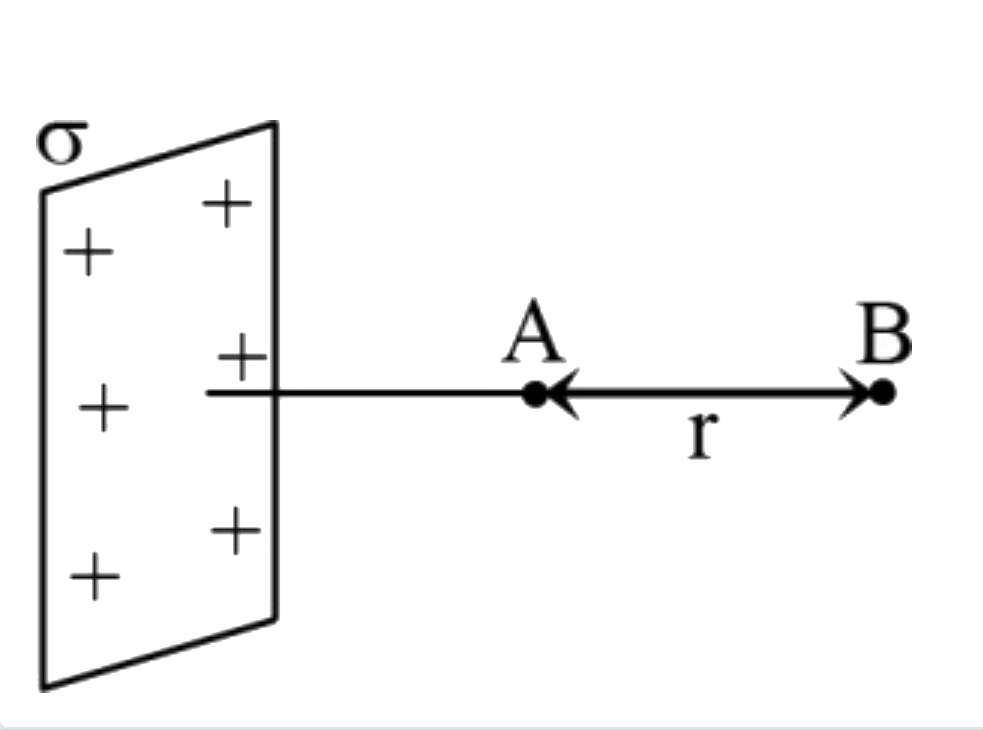 View Solution
View SolutionNature of equipotential surface for a point charge is
View SolutionElectric field intensity at a point due to an infinite sheet of charge having surface charge density σ is E.If sheet were conducting electric intensity would be
View SolutionA non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
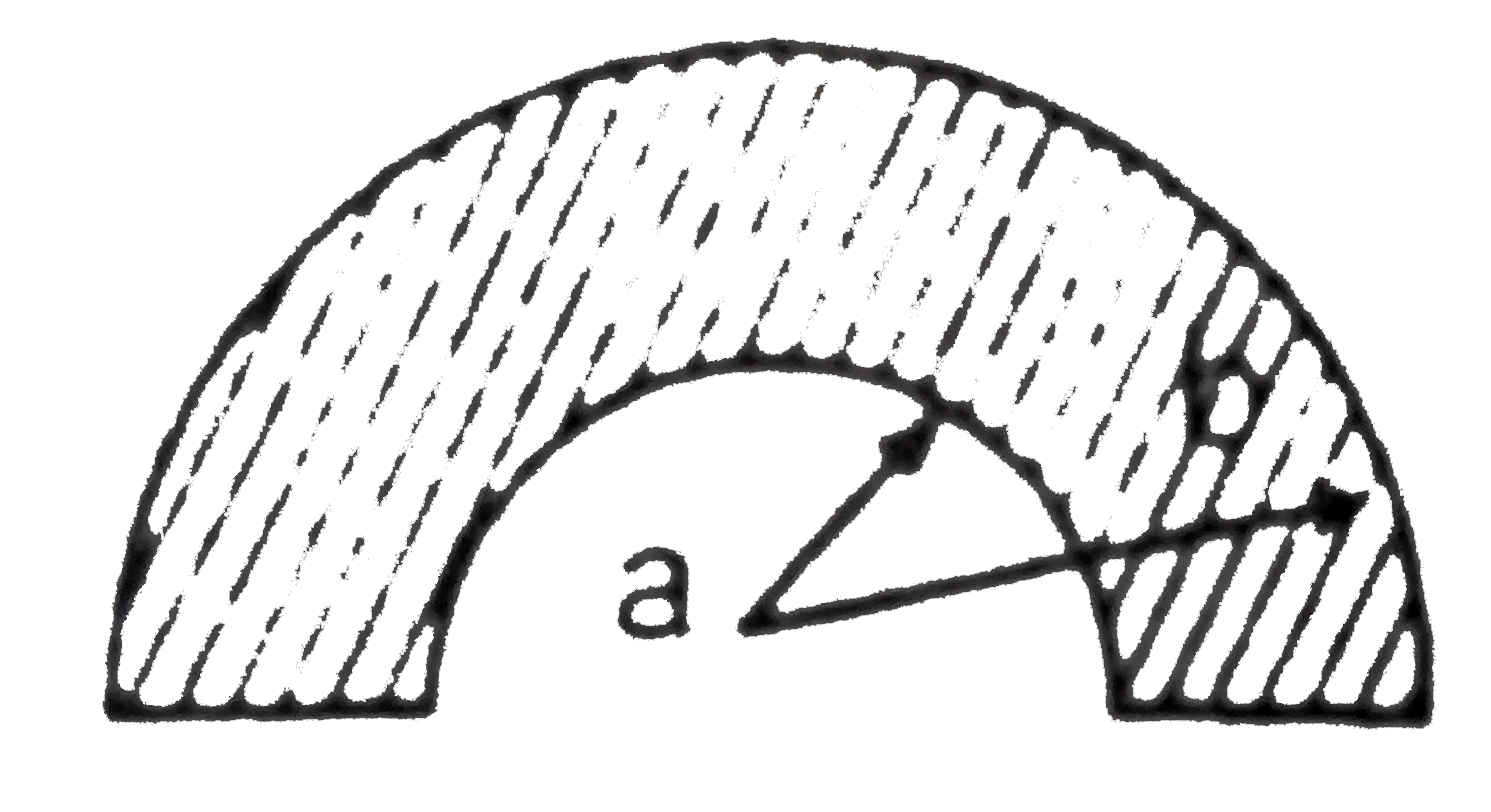 View Solution
View SolutionA spherical charged conductor has surface charge density σ.The intensity of electric field and potential on its surface are E and V .Now radius of sphere is halved keeping the charge density as constant .The new electric field on the surface and potential at the centre of the sphere are
View SolutionAn infinite thin non - conducting sheet has uniform surface charge density σ. Find the potential difference VA−VB between points A and B as shown in the figure. The line AB makes an angle of 37∘ with the normal to the sheet. (sin37∘=35)
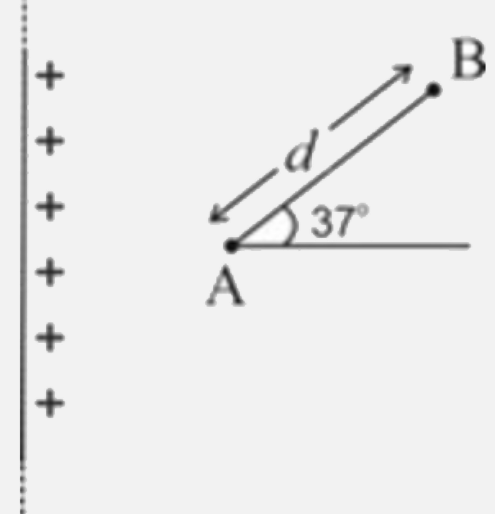 View Solution
View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surface of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surface is .
 View Solution
View Solution

