Electric field intensity at a point due to an infinite sheet of charge having surface charge density σ is E.If sheet were conducting electric intensity would be
2E
E
E2
none of these
The correct Answer is:B
To solve the problem of finding the electric field intensity at a point due to an infinite conducting sheet of charge, we can follow these steps:
Step 1: Understand the Electric Field due to an Infinite Sheet of Charge
For an infinite sheet of charge with surface charge density σ, the electric field intensity E at a point near the sheet is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
Step 2: Consider the Conducting Sheet
When the sheet is a conductor, the charges will redistribute themselves on the surface of the conductor. For an infinite conducting sheet, the charge will be distributed uniformly on both sides of the sheet.
Step 3: Apply Gauss's Law
To find the electric field due to the conducting sheet, we can use Gauss's Law. The electric field due to each side of the conducting sheet is:
Eone side=σ2ϵ0
Since the conducting sheet has charges on both sides, the total electric field Etotal at a point outside the conducting sheet will be:
Etotal=Eone side+Eone side=σ2ϵ0+σ2ϵ0=σϵ0
Step 4: Relate the Electric Field of the Conducting Sheet to the Original Electric Field
From our earlier step, we know that the electric field E due to the infinite sheet of charge is:
E=σ2ϵ0
Thus, the electric field due to the conducting sheet can be expressed as:
Econducting=2E
Step 5: Conclusion
Therefore, the electric field intensity at a point due to an infinite conducting sheet of charge is:
Econducting=2E
Final Answer
The electric field intensity if the sheet were conducting would be 2E.
---
For an infinite sheet of charge with surface charge density σ, the electric field intensity E at a point near the sheet is given by the formula:
E=σ2ϵ0
where ϵ0 is the permittivity of free space.
When the sheet is a conductor, the charges will redistribute themselves on the surface of the conductor. For an infinite conducting sheet, the charge will be distributed uniformly on both sides of the sheet.
To find the electric field due to the conducting sheet, we can use Gauss's Law. The electric field due to each side of the conducting sheet is:
Eone side=σ2ϵ0
Since the conducting sheet has charges on both sides, the total electric field Etotal at a point outside the conducting sheet will be:
Etotal=Eone side+Eone side=σ2ϵ0+σ2ϵ0=σϵ0
From our earlier step, we know that the electric field E due to the infinite sheet of charge is:
E=σ2ϵ0
Thus, the electric field due to the conducting sheet can be expressed as:
Econducting=2E
Therefore, the electric field intensity at a point due to an infinite conducting sheet of charge is:
Econducting=2E
The electric field intensity if the sheet were conducting would be 2E.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Part- II
20 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Part - IV
9 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Part - III
20 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Electric field intensity at a point in between two parallel sheets with like charges of same surface charge densities (σ) is
View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionDerive an expression for electric field intensity at a point due to point charge.
View SolutionAn infinite sheet of charge has surface charge density σ . The separation between two equipotential surfaces, whose potential differ by V is:
View SolutionThe electric field on two sides of a thin sheet of charge is shown in the figure. The charge density on the sheet is
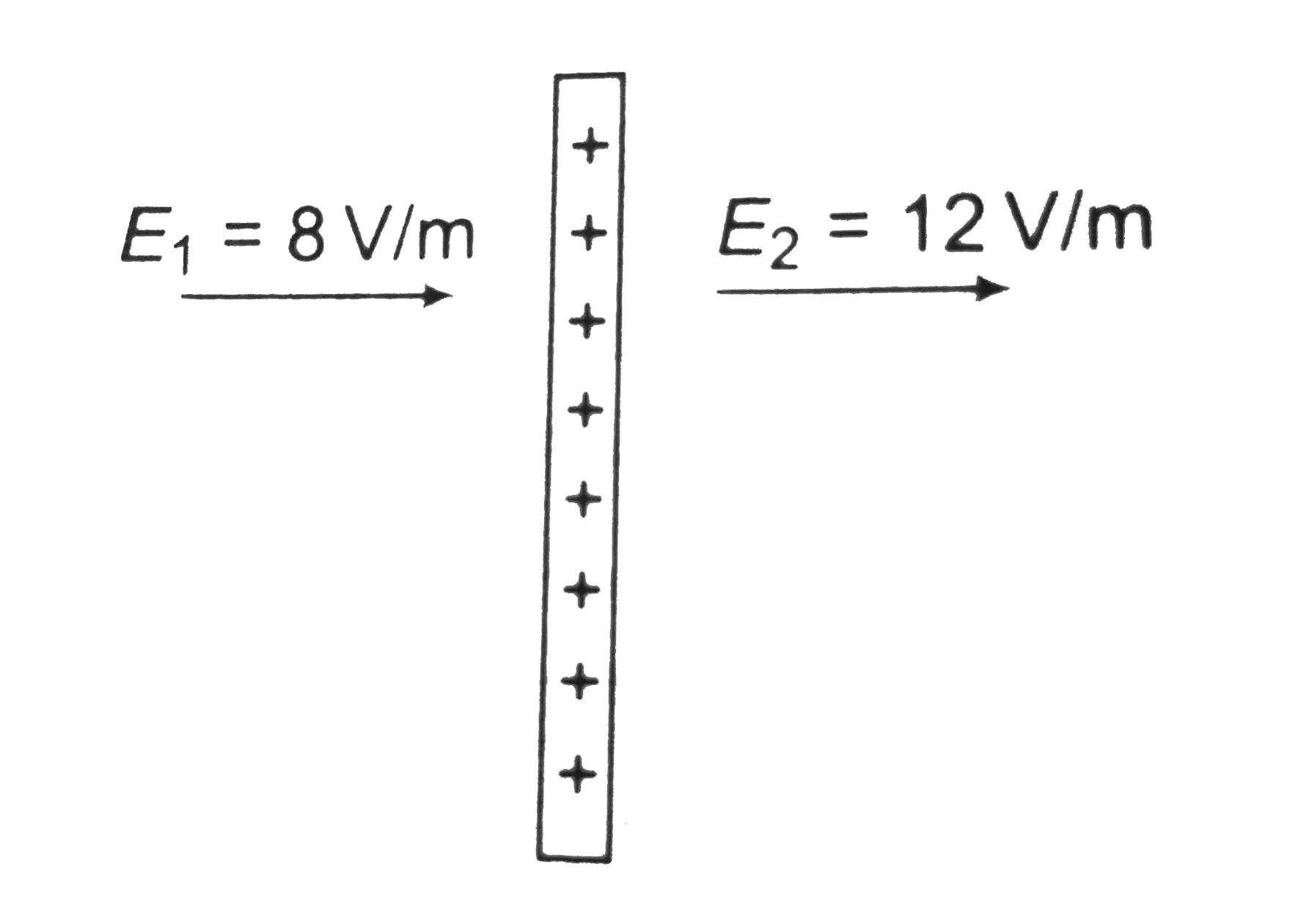
View SolutionThe electric field near a conducting surface having a uniform surface charge denstiy σ is given by
View SolutionThe magnitude of the electric field on the surface of a sphere of radius r having a uniform surface charge density σ is
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View Solution(a) Using Gauss's law, derive an expression for the electric field intensity at any point outside a uniformly charged thin spherical shell of radius R and charge density σC/m2. Draw the field lines when the charge density of the sphere is (i) positive, (ii) negative.
(b) A uniformly charged conducting sphere of 2.5 m in diameter has a surface charge density of 100 μC/m2. Calculate the
(i) charge on the sphere
(ii) total electric flux passing through the sphere.
View SolutionFigure shows a long wire having uniform charge density λ as shown in figure. Calculate electric field intensity at point P.
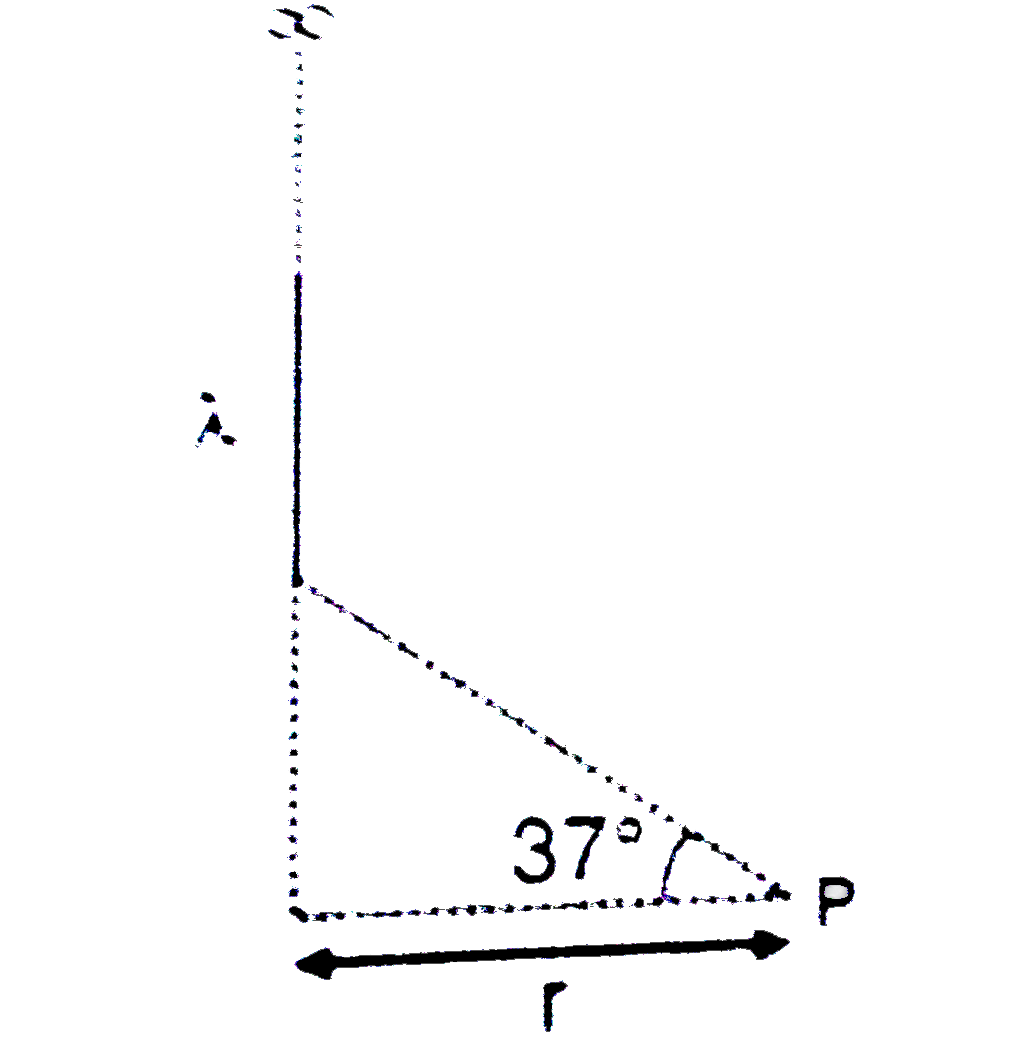
View Solution
