In the circuit shown, E=18kV,C=10μF,R1=4MΩ,R2=6MΩ,R3=3MΩ with C completely uncharged, switch S is suddenly closed (at t=0).
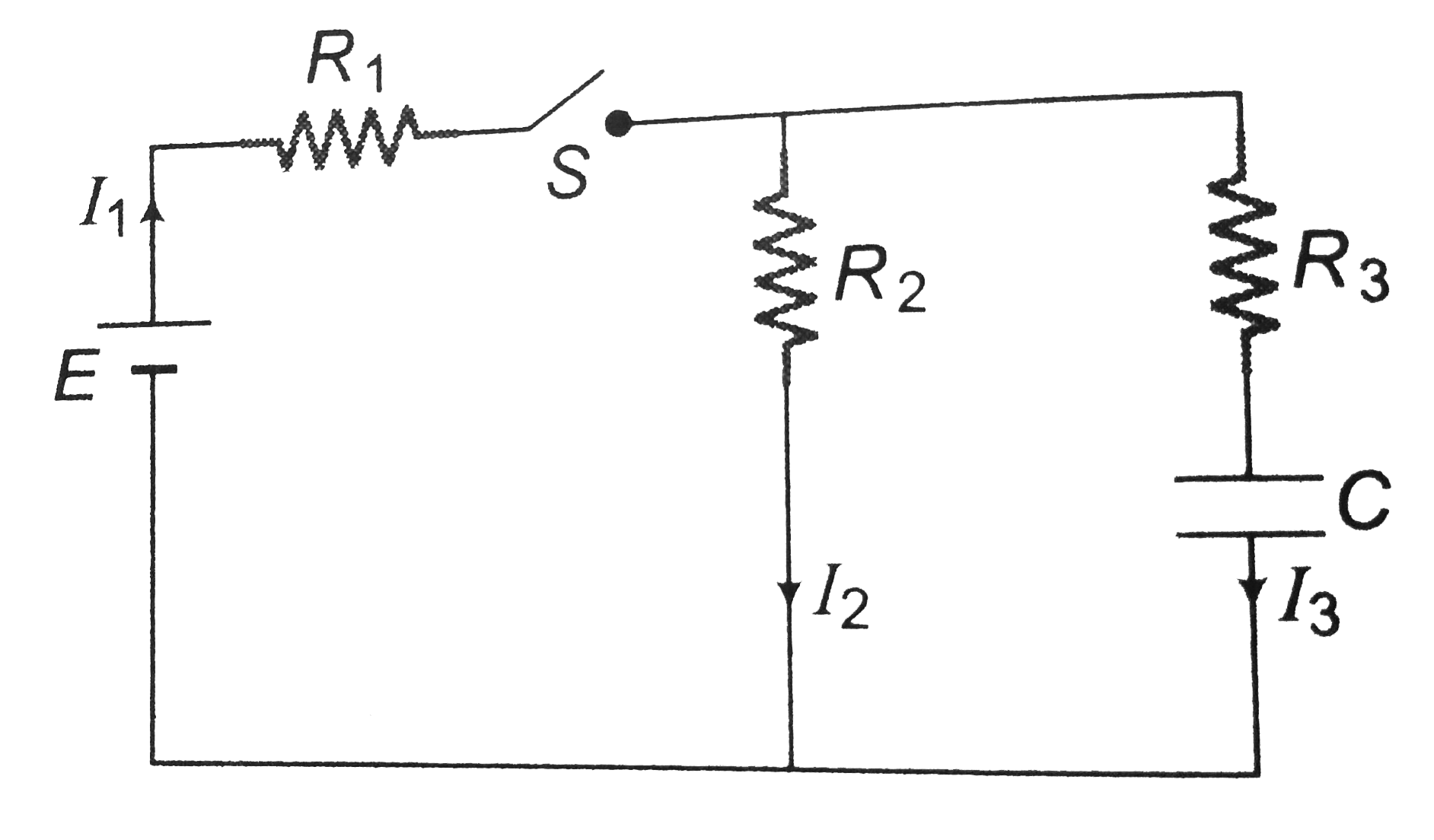
(a) Determine the current through each resistor for t=0 and t=∞
(b) What are the values of V2 (potential difference across R2) at t=0 and t=∞. ?
(c) Plot a graph of the potential differenceV2 versus t and determine the instantaneous value of V2.
At t=0, when capacitor is uncharged, its equivalent resistance is zero.
∴Rnet=4+6×36+3=6MΩ
or i1=18×1036×106A=3mA
This will distribute in inverse ratio of resistance,
∴i2=36+3i1=1mA and i3=2mA
At t=∞ when capcitor is completely charged, equivalent resistance of capacitgor is infinite
i3=0,i1=i2=18×103(4+6)×106=1.8mA
b. At t=0
V2=i2R2=(1×10−3)(6×106)V
=6kV
At t=∞
V2=i2R2=(1.8×106−3)(6×106)V
=10.8kV
c. to find time constant of the circuit we will have to short circuit the battery and find resistance across capacitor. In that case R1 and R2 are in parallel and they are in series with R3. 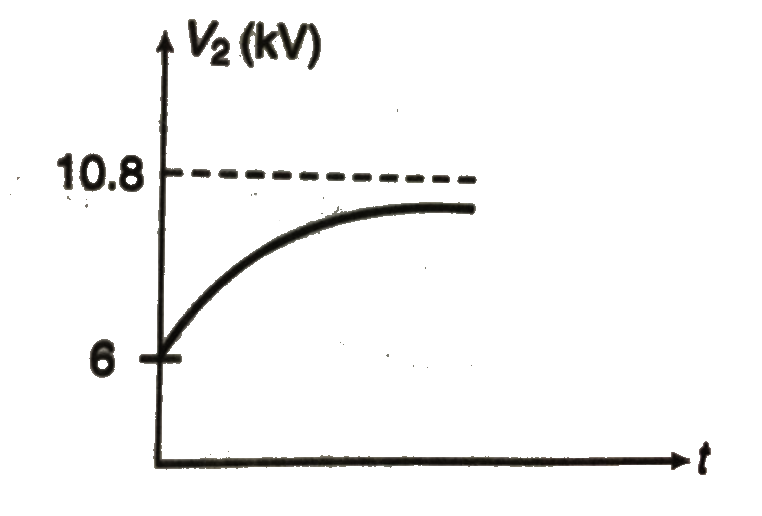
∴Rnet=3+4×64+6=5.4MΩ
∴τC=CR≠t=(10×10−6)(5.4×106)
=54s
∴V2=6+(10.8−6)(1−e−tC)
=6+4.8(1−et54)
Here, V2 is in kV and t is second.
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Switch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionThe switch S is closed in the circuit shown at time t=0 . The current in the resistor at t=0 and t=∞ are respectively .
View SolutionIn the circuit shown, switch S is closed at time t=0. Find the current through the inductor as a function of time t.

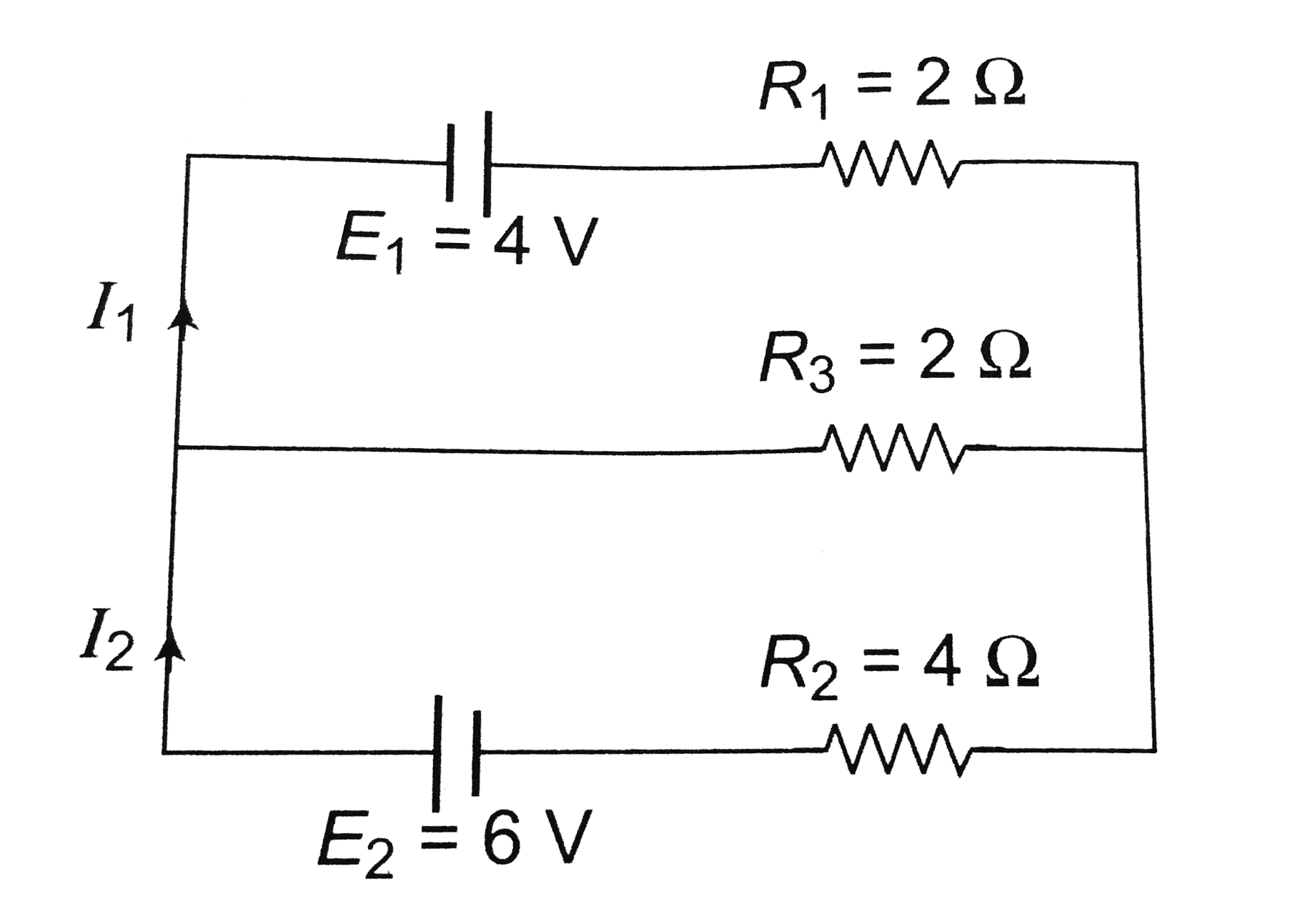
View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
View SolutionIn the given at t=0, switch S is closed.
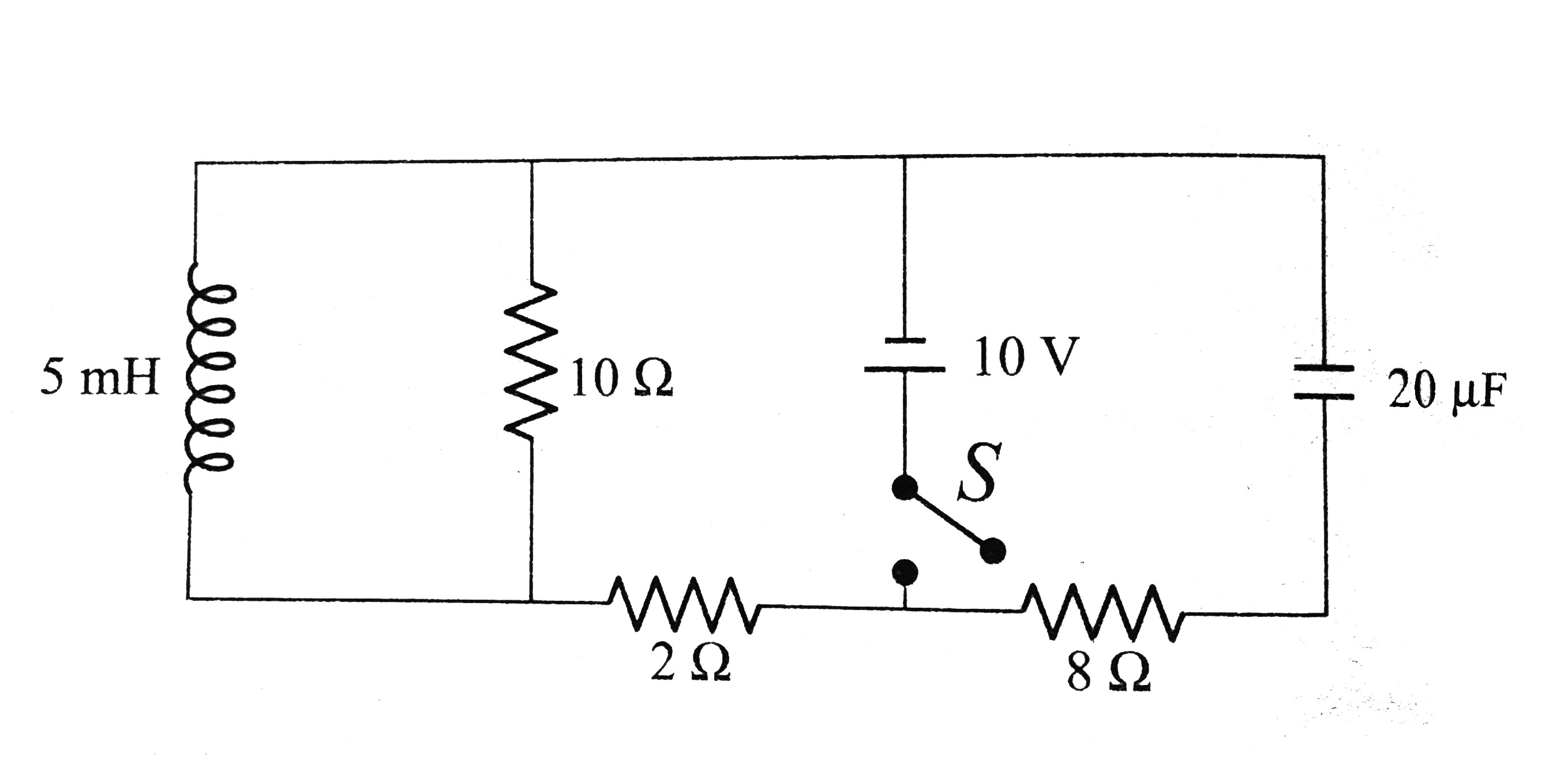
The current through the 10Ω resistor at any instant t(0<t<∞) will be
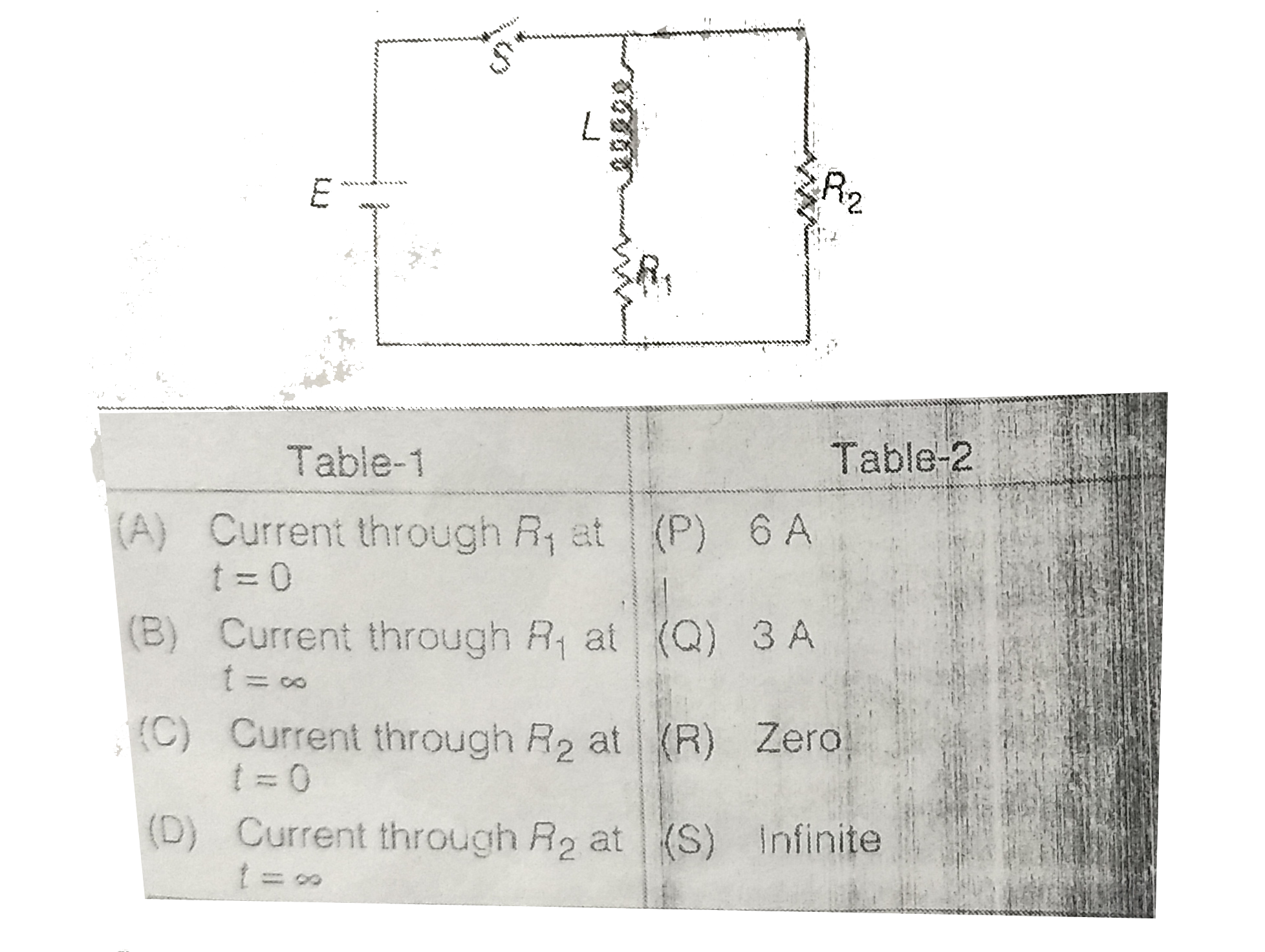
View SolutionIn the circuit diagram shown in Figure E=18V , L=2H, R1=3Ω,R2=6Ω. Switch S is closed at t=0 Match the following:
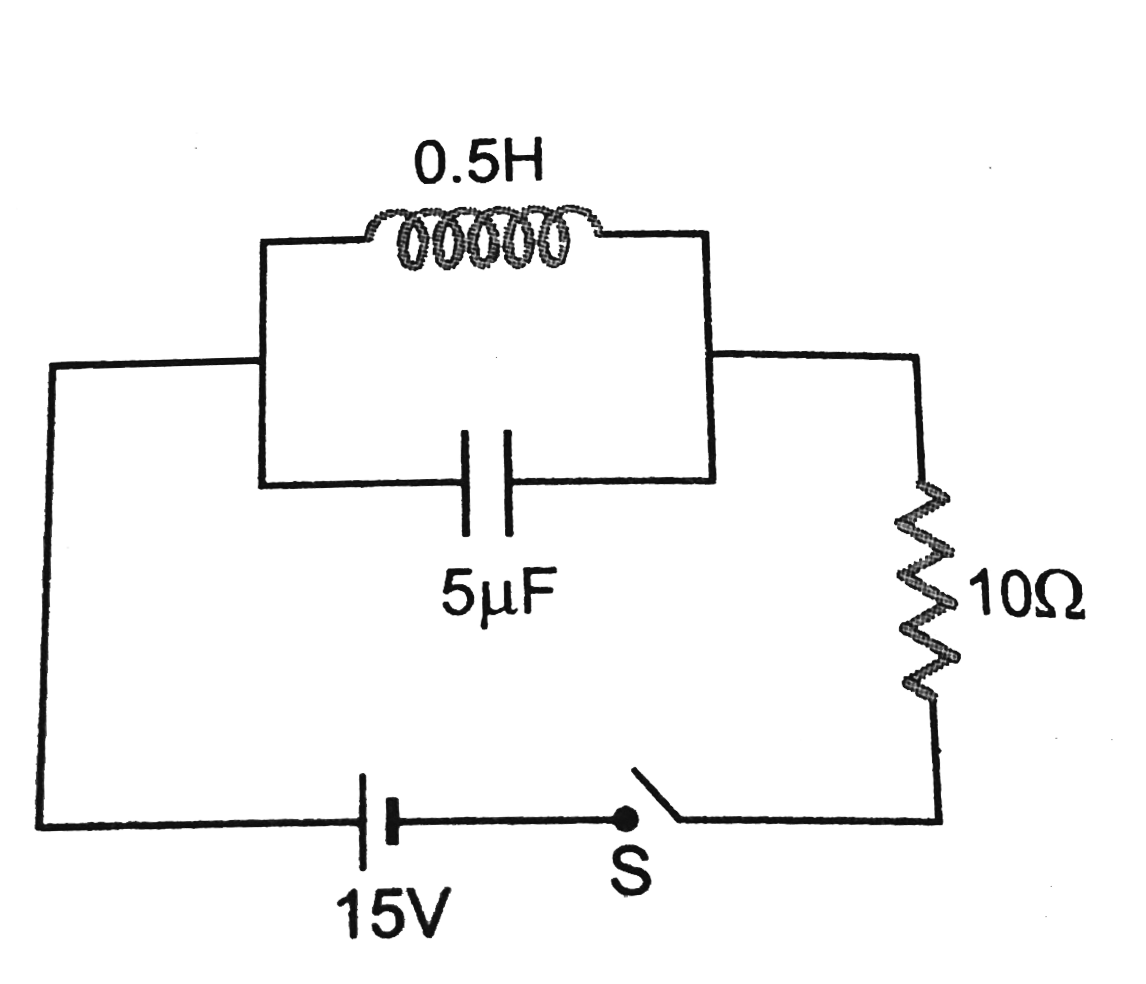
View SolutionIn the circuit shown in Fig. currrent through the battery at t=0 and t=∞ is
View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
View SolutionThe switch shown in figure is closed at t=0 find the charge throuh battery till time t=LR
_2019_CBT8_E01_016_Q01.png)
View SolutionIn the circuit shown the key (K) is closed at t=0, the current through the key at the instant t=10−3ln,2 is

View Solution
