A spherical capacitor has the inner sphere of radius 2cm and the outerone of 4cm. If the inner sphere is earthed and the outer one is charged with a charge of 2μC and isolated. Calculate ltbr> (a) the potential to which the outer sphere is raised.
(b) the charge retained on the outer surface of the outer sphere.
The correct Answer is:A, C
To solve the problem step by step, we will break it down into two parts as required:
Part (a): Calculate the potential to which the outer sphere is raised.
1. Identify the given values:
- Radius of the inner sphere, r1=2cm=0.02m
- Radius of the outer sphere, r2=4cm=0.04m
- Charge on the outer sphere, Qouter=2μC=2×10−6C
- The inner sphere is earthed, so its potential is Vinner=0.
2. Use the formula for potential due to a charged sphere:
The potential V at a distance r from a point charge Q is given by:
V=kQr
where k=9×109N m2/C2.
3. Set up the equation for the potential at the inner sphere:
Since the inner sphere is earthed, its potential is zero:
Vinner=kQinnerr1+kQouterr2=0
4. Let the charge on the inner sphere be Qinner:
0=kQinner0.02+k(2×10−6)0.04
5. Simplify the equation:
0=Qinner0.02+2×10−60.04
0=Qinner0.02+5×10−5
Qinner=−1×10−6C=−1μC
6. Calculate the potential of the outer sphere:
The potential at the outer sphere is given by:
Vouter=kQenclosedr2
where Qenclosed=Qouter+Qinner=2×10−6−1×10−6=1×10−6C.
7. Plug in the values:
Vouter=(9×109)(1×10−6)0.04
Vouter=9×1030.04=225000V=2.25×105V
Part (b): Calculate the charge retained on the outer surface of the outer sphere.
1. Determine the charge on the outer surface:
The total charge on the outer sphere is Qouter=2μC. The charge on the inner sphere is Qinner=−1μC.
2. Use the principle of conservation of charge:
The charge on the outer surface can be calculated as:
Qouter surface=Qouter−Qinner
Qouter surface=2×10−6−(−1×10−6)=2×10−6+1×10−6=3×10−6C=1μC
Final Answers:
- (a) The potential to which the outer sphere is raised is 2.25×105V.
- (b) The charge retained on the outer surface of the outer sphere is 1μC.
- Radius of the inner sphere, r1=2cm=0.02m
- Radius of the outer sphere, r2=4cm=0.04m
- Charge on the outer sphere, Qouter=2μC=2×10−6C
- The inner sphere is earthed, so its potential is Vinner=0.
The potential V at a distance r from a point charge Q is given by:
V=kQr
where k=9×109N m2/C2.
Since the inner sphere is earthed, its potential is zero:
Vinner=kQinnerr1+kQouterr2=0
0=kQinner0.02+k(2×10−6)0.04
0=Qinner0.02+2×10−60.04
0=Qinner0.02+5×10−5
Qinner=−1×10−6C=−1μC
The potential at the outer sphere is given by:
Vouter=kQenclosedr2
where Qenclosed=Qouter+Qinner=2×10−6−1×10−6=1×10−6C.
Vouter=(9×109)(1×10−6)0.04
Vouter=9×1030.04=225000V=2.25×105V
The total charge on the outer sphere is Qouter=2μC. The charge on the inner sphere is Qinner=−1μC.
The charge on the outer surface can be calculated as:
Qouter surface=Qouter−Qinner
Qouter surface=2×10−6−(−1×10−6)=2×10−6+1×10−6=3×10−6C=1μC
- (a) The potential to which the outer sphere is raised is 2.25×105V.
- (b) The charge retained on the outer surface of the outer sphere is 1μC.
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Video
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
A sherical capacitor has an inner sphere of radius 12cm and an outer spere of radius 13cm. The outer sphere is earthed, and the inner sphere is given a charge of 2.5μC. The space between the concentric spjheres is filled with a liquid of dielectric caonstant 32. Determine the potential of the inner sphere.
View SolutionA spherical capacitor has an inner sphere of radius 12 cm and an outer sphere of radius 13 cm. The outer sphere is earthed and the inner sphere is given a charge of 2.5μC. The space between the concentric spheres is filled with a liquid of dielectric constant 32.
(a) Determine the capacitance of the capacitor. (b) What is the potential of the inner sphere ?
(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius 12 cm.Explain why the later is much smaller ?
View SolutionCapacity of a spherical capacitor is C1 when inner sphere is charged and outer sphere is earthed and C2 when inner sphere is earthed and outer sphere charged. Then C1C2 is (a = radius of inner sphere b = radius of outer sphere)
View SolutionTwo concentric spheres of radii R and 2R are charged. The inner sphere has a charge if 1μC and the outer sphere has a charge of 2μC of the same sigh. The potential is 9000V at a distance 3R from the common centre. The value of R is
View SolutionA point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionIn (Fig. 3.73), if the inner shell has charge +q0 and the outer shell is earthed, then
 .
.
i. determine the charge on the outer shell, and
ii. find the potential of the inner shell.
View SolutionConsider two concentric metal spheres. The outer sphere is given a charge Q>0, then
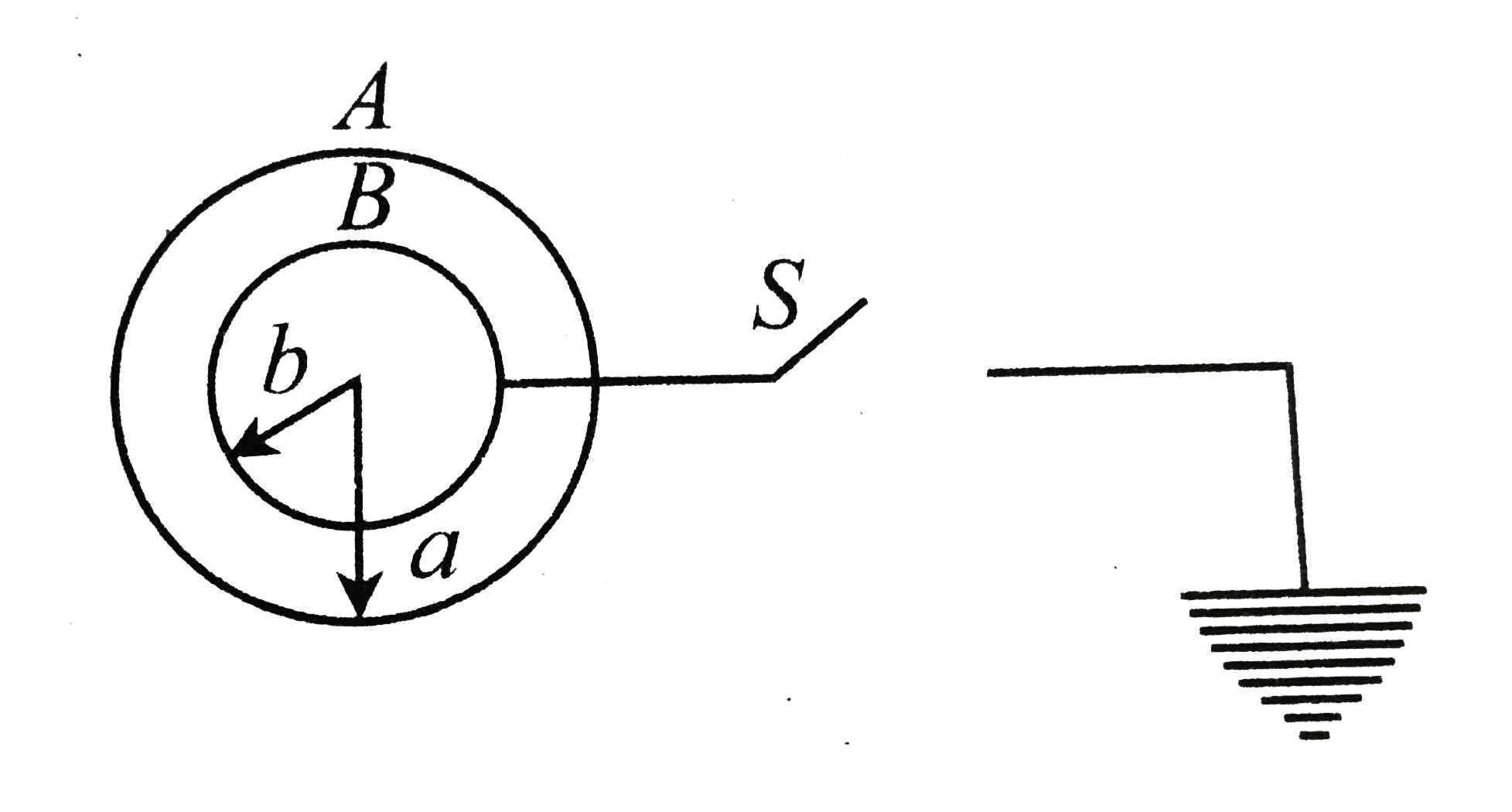 ,
,
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionA sphere of 4cm radius is suspended within a hollow sphere of 6cm radius. The inner sphere is charged to potential 3 e.s.u. and the outer sphere is earthed. The charge on the inner sphere is
View SolutionA sphere of radius 0.03m is suspended within a hollow sphere of radius 0.05m. If the inner sphere is charged to a potential of 1500 volt and outer sphere is earthed. Find the capacitance and the charge of the inner sphere.
View Solution