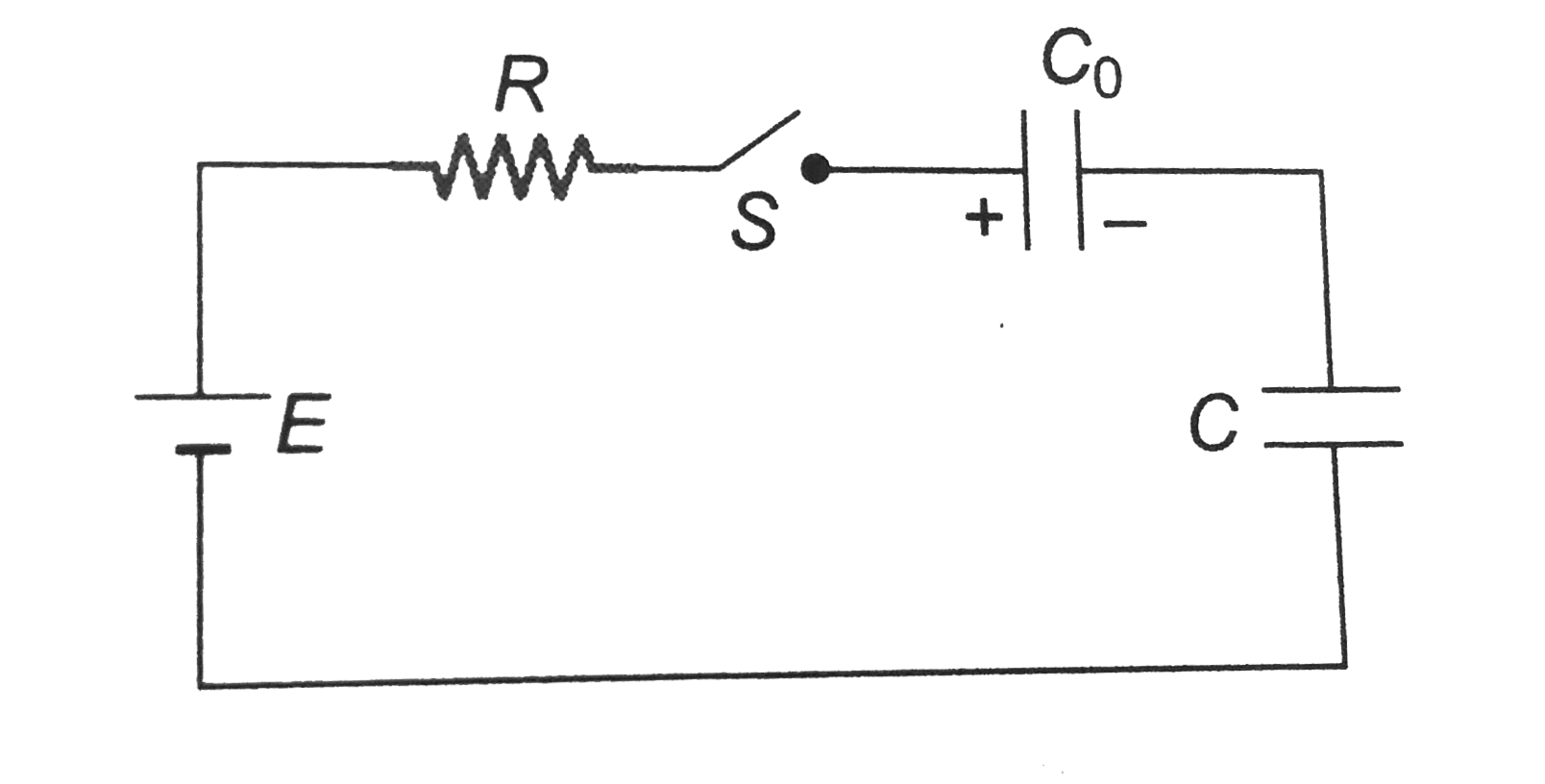
The switch S is closed at t=0 . the capacitor C is uncharged but C0 has a charge Q0=2μC at t=0. If =100Ommega , C=2μF , C0=2μF,E=4V. Calculate i(t) in the circuit.
The correct Answer is:A, C, D
At t=0 capacitor C0 is like a battery of
emf =Q0C0=1V
Net emf of the circfuit =4−1=3V
total resistance is R=100Ω
∴ Initial current 3100=0.03A
This current will decrease exponentially to zero.
∴i=0.03e−tτC
Here, τC=CnetR=(1×10−6)(100)
=10−4s
∴i=0.03e−104t
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
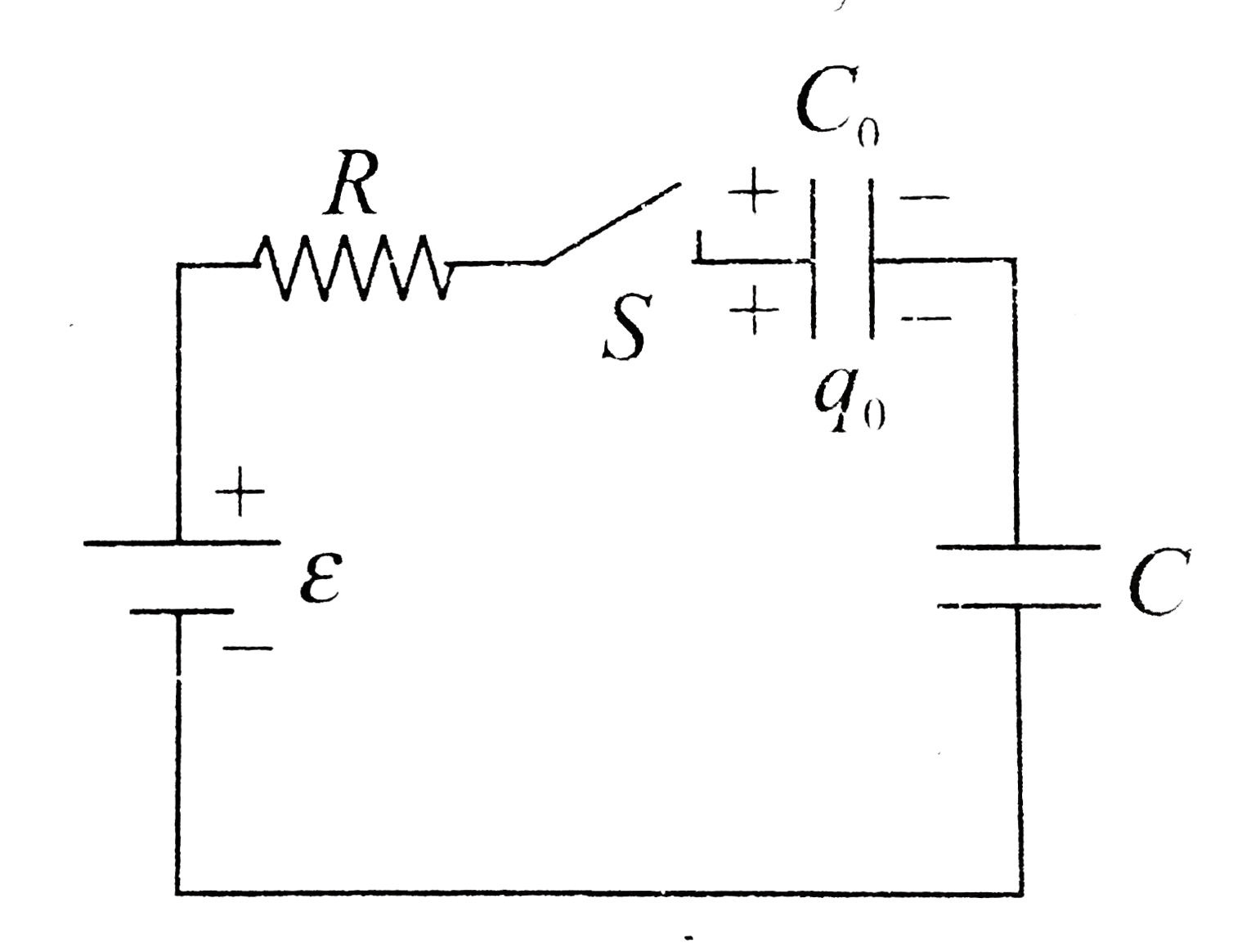
The switch S is closed aty t = 0. the capacitor C is uncharged but C0 has a charge q0 at t =0. Calculate the current i(t) in the circuit
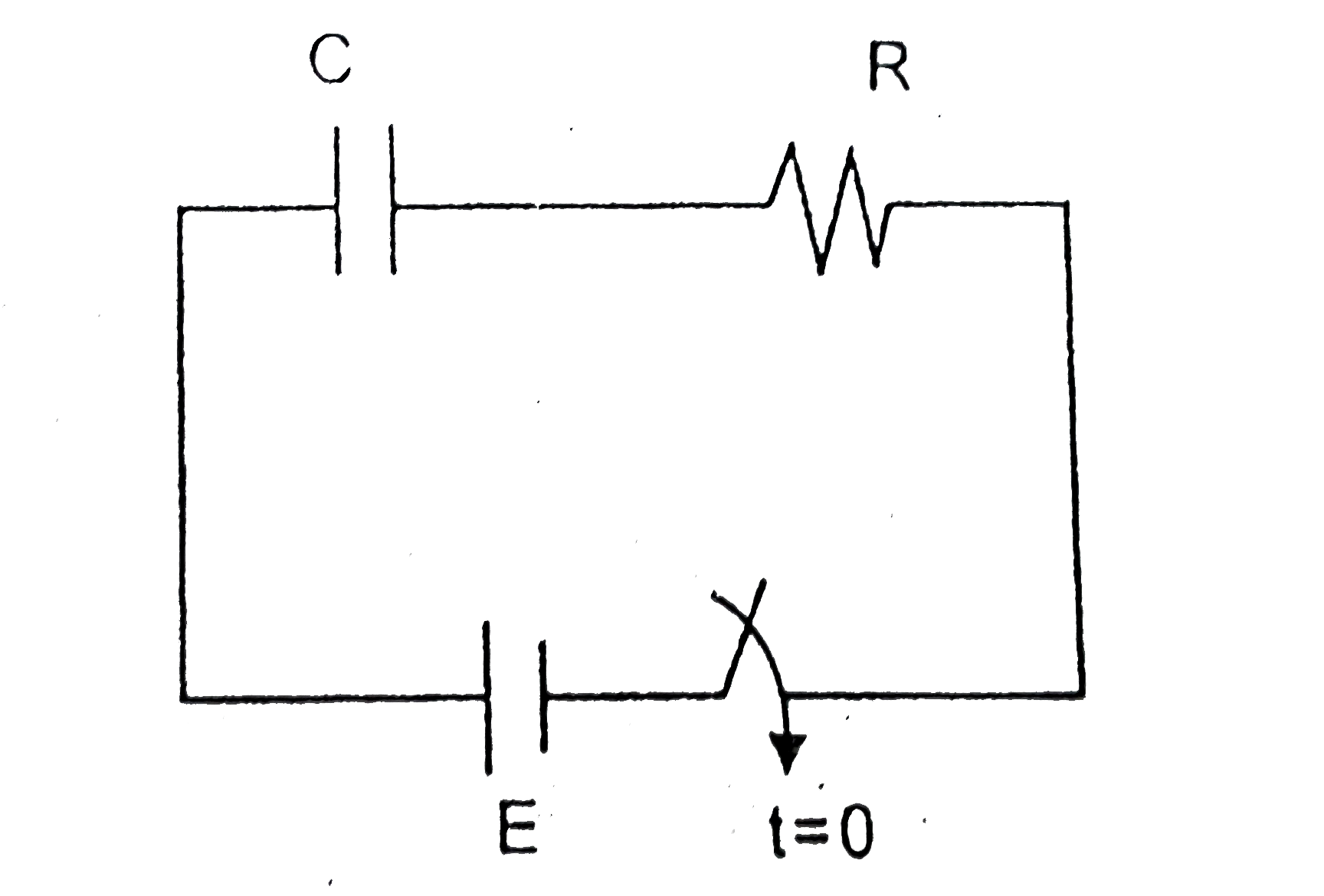
View SolutionIn the circuit shown key is closed at t=0 with capacitor initially uncharged.
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
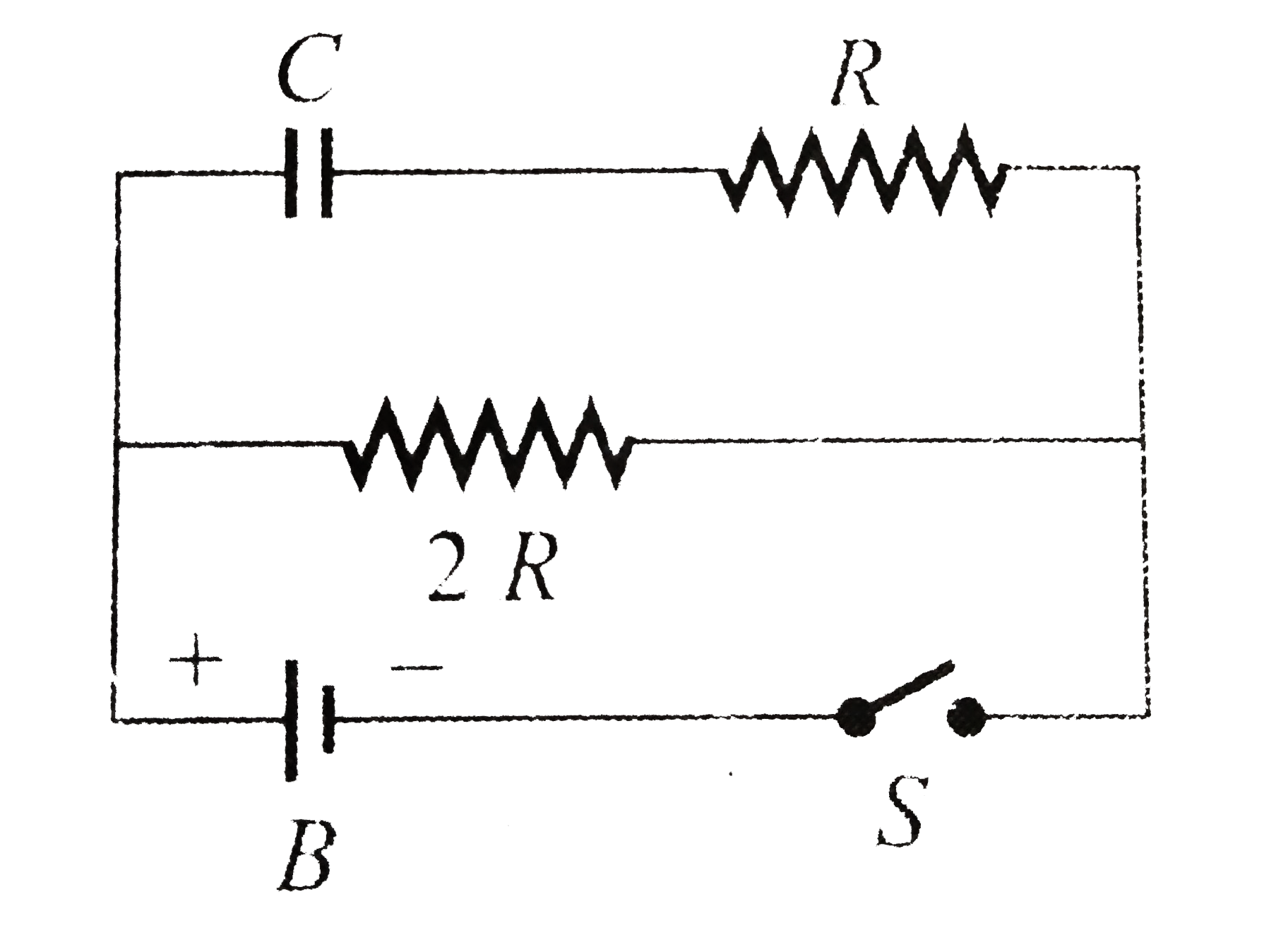
View SolutionThe switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
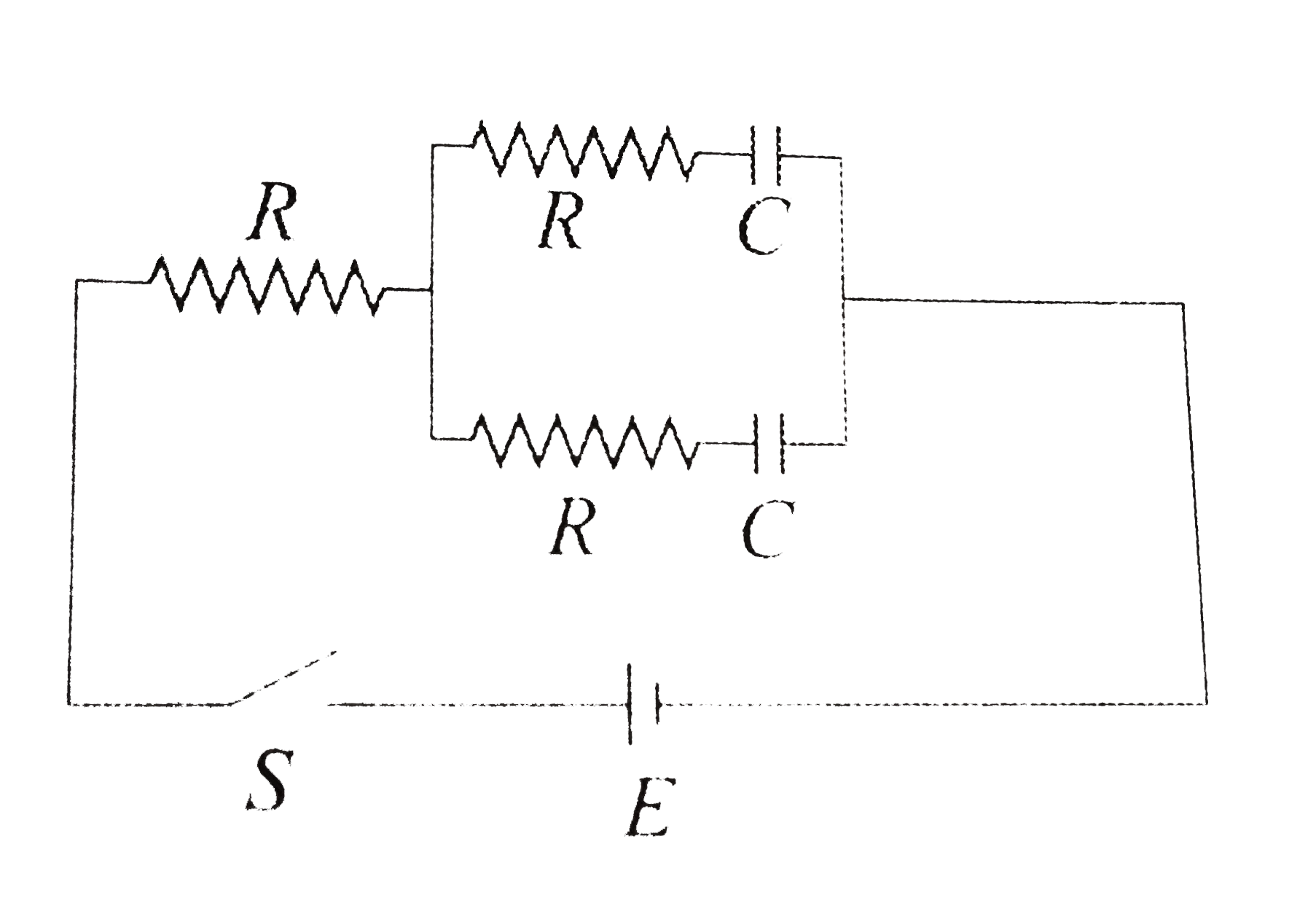
View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
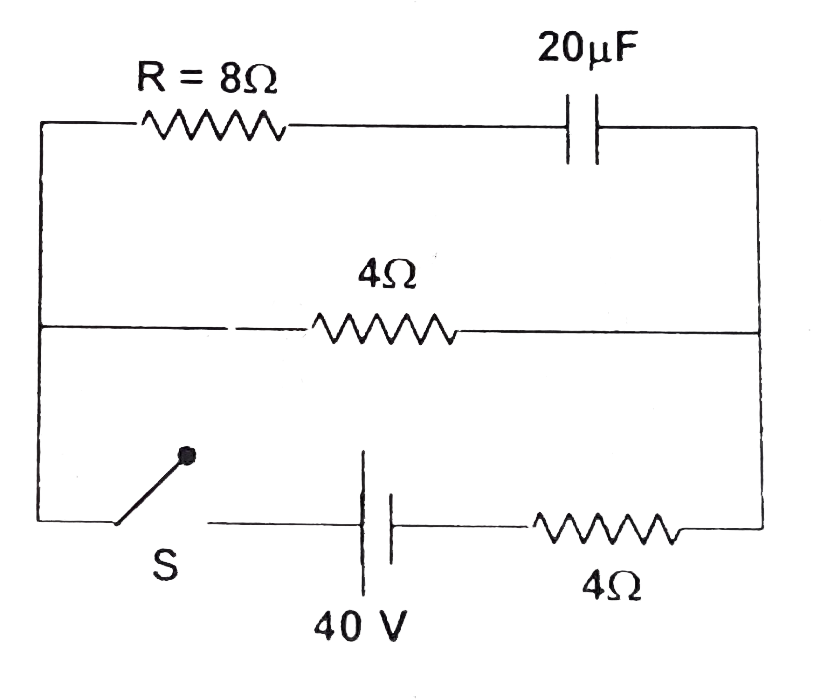
View SolutionIn the circuit shown, the switch 'S' is closed at t=0. Then capacitor is initially uncharged. Then the current through the resistor R=8Ω at t=0.4×10−3sec is (Take e−2=0.135 )
View SolutionFor the arrangement shown in the figure, the switch is closed at t=0. C2 is initially uncharged while C1 has a charge of 2μC
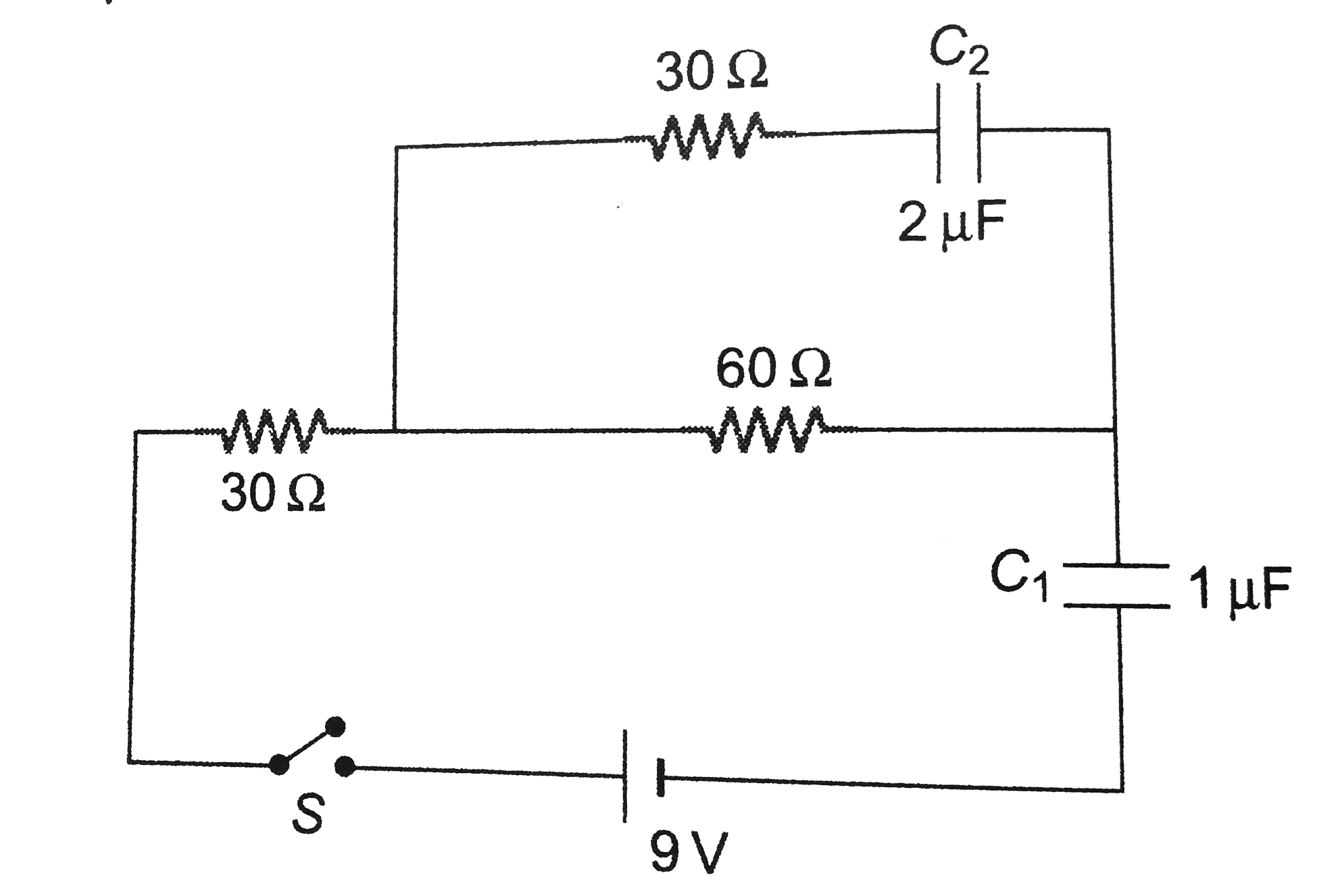
(a) Find the current comingn out of the battery just after the switch is closed.
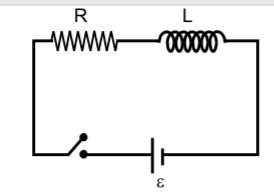
(b) Find the charge on the capacitors in the steady state condition.View SolutionIn the given circuit switch is closed at t=0. The charge flown in time t=Tc (where Tc is time constant).
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
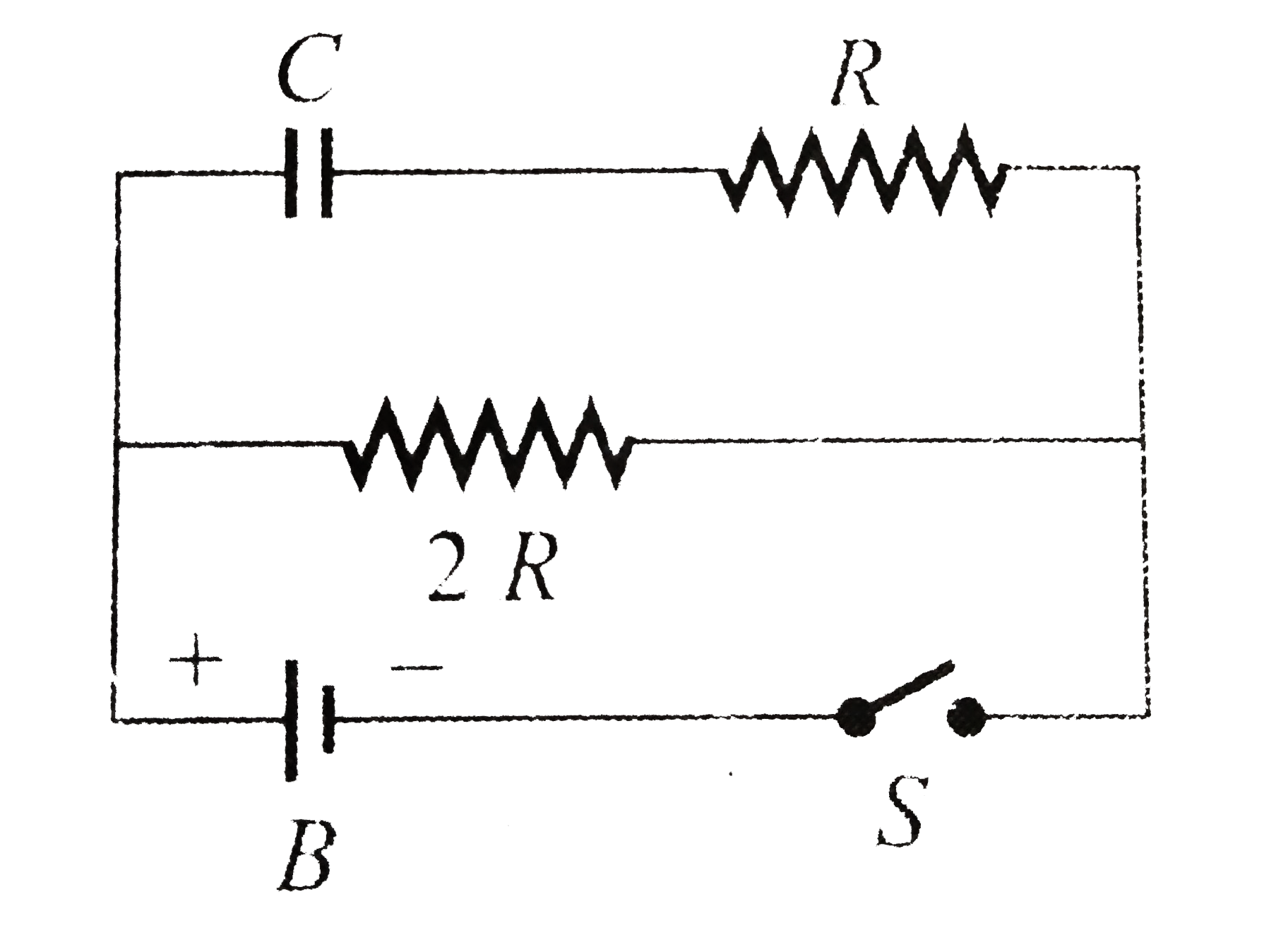
View SolutionThe switch S is closed in the circuit shown at time t=0 . The current in the resistor at t=0 and t=∞ are respectively .
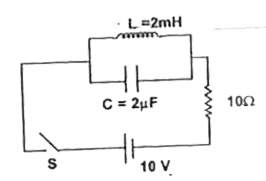
View Solution