Three infinitely long thin wires, each carrying current i in the same dieretion, are the xy plane of a gravity free space. The central wire is along the y-axis while the other two are along
i find the locus of the points for which the magnetic field is zero.
ii If the central wire is displaced along the -direction by a small amount and released, show that it will execute simple harmonic motion. If the linear mass density of the wires is , find the frequency of oscillation.
To solve the given problem step by step, we will break it down into two parts as specified in the question.
Part (i): Finding the locus of points where the magnetic field B is zero
1. Understanding the Setup:
- We have three infinitely long wires carrying current I in the same direction.
- The central wire is along the y-axis, while the other two wires are located at x=+d and x=−d.
2. Magnetic Field Due to a Long Straight Wire:
- The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
- The direction of the magnetic field follows the right-hand rule.
3. Calculating Magnetic Fields:
- Let’s denote the wires as follows:
- Wire 1 (at x=−d): B1
- Wire 2 (at x=+d): B2
- Central Wire (at x=0): B3
- The magnetic field at a point P(x,0) due to each wire:
- For Wire 1 (at x=−d):
B1=μ0I2π(d+x)(directed out of the page)
- For Wire 2 (at x=+d):
B2=μ0I2π(d−x)(directed into the page)
4. Setting Up the Equation for Zero Magnetic Field:
- For the magnetic field to be zero at point P:
B1−B2=0⟹μ0I2π(d+x)=μ0I2π(d−x)
- Simplifying this equation leads to:
1d+x=1d−x
5. Cross Multiplying and Solving:
- Cross-multiplying gives:
(d−x)=(d+x)
- Rearranging leads to:
2x=0⟹x=0
- This indicates that the magnetic field is zero at the midpoint between the two wires.
6. Finding Other Points:
- To find other points, we can analyze the magnetic field strengths at points along the x-axis and find that:
x=±d√3
- Thus, the locus of points where the magnetic field is zero is:
x=±d√3,y=0
Part (ii): Showing SHM and Finding Frequency of Oscillation
1. Displacing the Central Wire:
- If the central wire is displaced a small distance z along the z-axis, we need to analyze the forces acting on it due to the other two wires.
2. Restoring Force:
- The magnetic forces acting on the central wire will create a restoring force. The force F on the central wire due to the other two wires can be expressed as:
F=kz
- Here, k is a constant that we will determine.
3. Calculating the Restoring Force:
- The magnetic field at the central wire due to the other two wires will create a force that acts to restore it to equilibrium. The net force can be derived from the magnetic field interactions.
4. Using the Formula for Frequency:
- The angular frequency ω of the simple harmonic motion is given by:
ω=√km
- Where m is the mass of the wire segment, which can be expressed in terms of linear mass density λ.
5. Finding k:
- The expression for k can be derived from the magnetic field interactions, leading to:
k=μ0I22πd2
6. Finding the Frequency:
- The frequency f can be calculated as:
f=12π√km=12π√μ0I22πd2λ
Final Answers:
- Locus of Points Where Magnetic Field is Zero: x=±d√3,y=0
- Frequency of Oscillation:
f=12π√μ0I22πd2λ
- We have three infinitely long wires carrying current I in the same direction.
- The central wire is along the y-axis, while the other two wires are located at x=+d and x=−d.
- The magnetic field B at a distance r from a long straight wire carrying current I is given by:
B=μ0I2πr
- The direction of the magnetic field follows the right-hand rule.
- Let’s denote the wires as follows:
- Wire 1 (at x=−d): B1
- Wire 2 (at x=+d): B2
- Central Wire (at x=0): B3
- The magnetic field at a point P(x,0) due to each wire:
- For Wire 1 (at x=−d):
B1=μ0I2π(d+x)(directed out of the page)
- For Wire 2 (at x=+d):
B2=μ0I2π(d−x)(directed into the page)
- For the magnetic field to be zero at point P:
B1−B2=0⟹μ0I2π(d+x)=μ0I2π(d−x)
- Simplifying this equation leads to:
1d+x=1d−x
- Cross-multiplying gives:
(d−x)=(d+x)
- Rearranging leads to:
2x=0⟹x=0
- This indicates that the magnetic field is zero at the midpoint between the two wires.
- To find other points, we can analyze the magnetic field strengths at points along the x-axis and find that:
x=±d√3
- Thus, the locus of points where the magnetic field is zero is:
x=±d√3,y=0
- If the central wire is displaced a small distance z along the z-axis, we need to analyze the forces acting on it due to the other two wires.
- The magnetic forces acting on the central wire will create a restoring force. The force F on the central wire due to the other two wires can be expressed as:
F=kz
- Here, k is a constant that we will determine.
- The magnetic field at the central wire due to the other two wires will create a force that acts to restore it to equilibrium. The net force can be derived from the magnetic field interactions.
- The angular frequency ω of the simple harmonic motion is given by:
ω=√km
- Where m is the mass of the wire segment, which can be expressed in terms of linear mass density λ.
- The expression for k can be derived from the magnetic field interactions, leading to:
k=μ0I22πd2
- The frequency f can be calculated as:
f=12π√km=12π√μ0I22πd2λ
- Locus of Points Where Magnetic Field is Zero: x=±d√3,y=0
- Frequency of Oscillation:
f=12π√μ0I22πd2λ
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
Three infinitely long thin wires each carrying current I in the same direction are in x−y plane of a gravity free space. The central wire is along the y-axis while the other two are along x=±d. If the central wire is slightly displaced along z-axis and released, show that it will execute S.H.M. The linear mass density of the wire is λ. If the time period of this small oscillation is kπdI√πλμ0, then find the value of k.
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
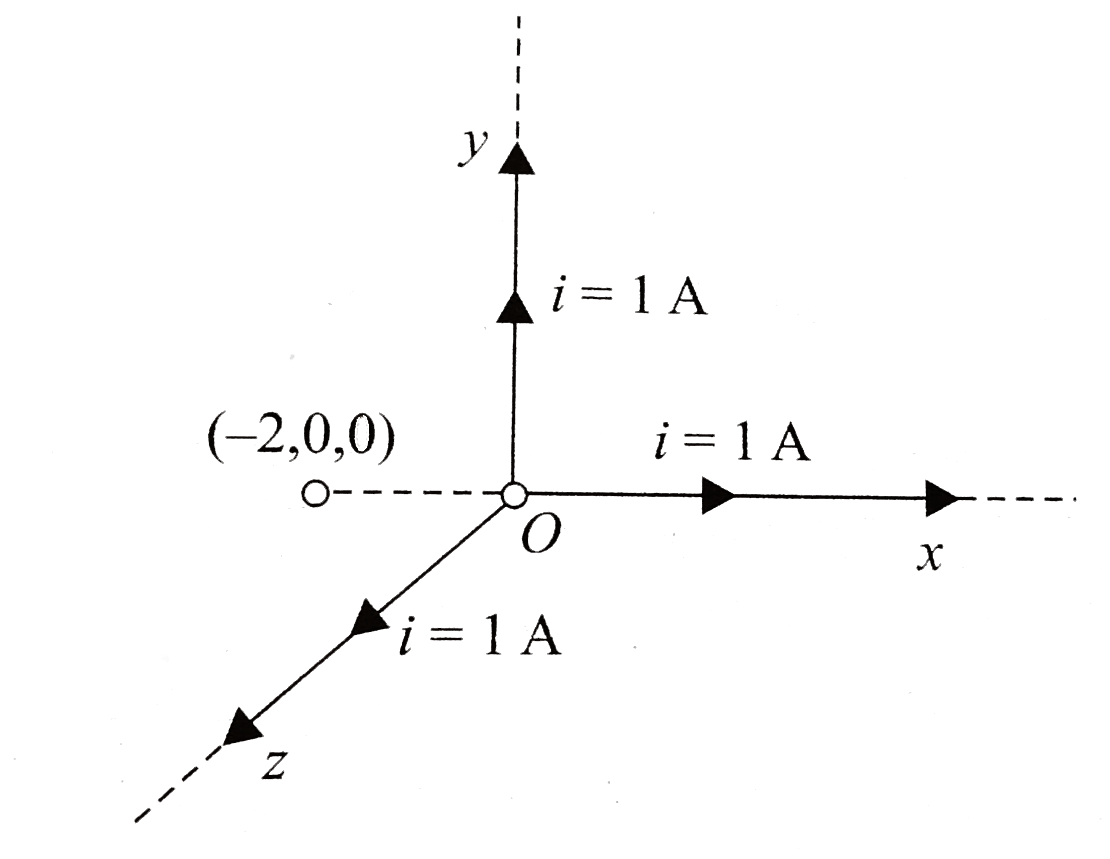
View SolutionTwo perpendicular infinite wires are carrying current i as shown in the figure. The magnetic field at point P is :
_2019_CBT2_E01_008_Q01.png)
View Solutiontwo infinite wires, carrying currents i1andi2., are lying along x-and y-axes, as shown in the x-y plane. Then,
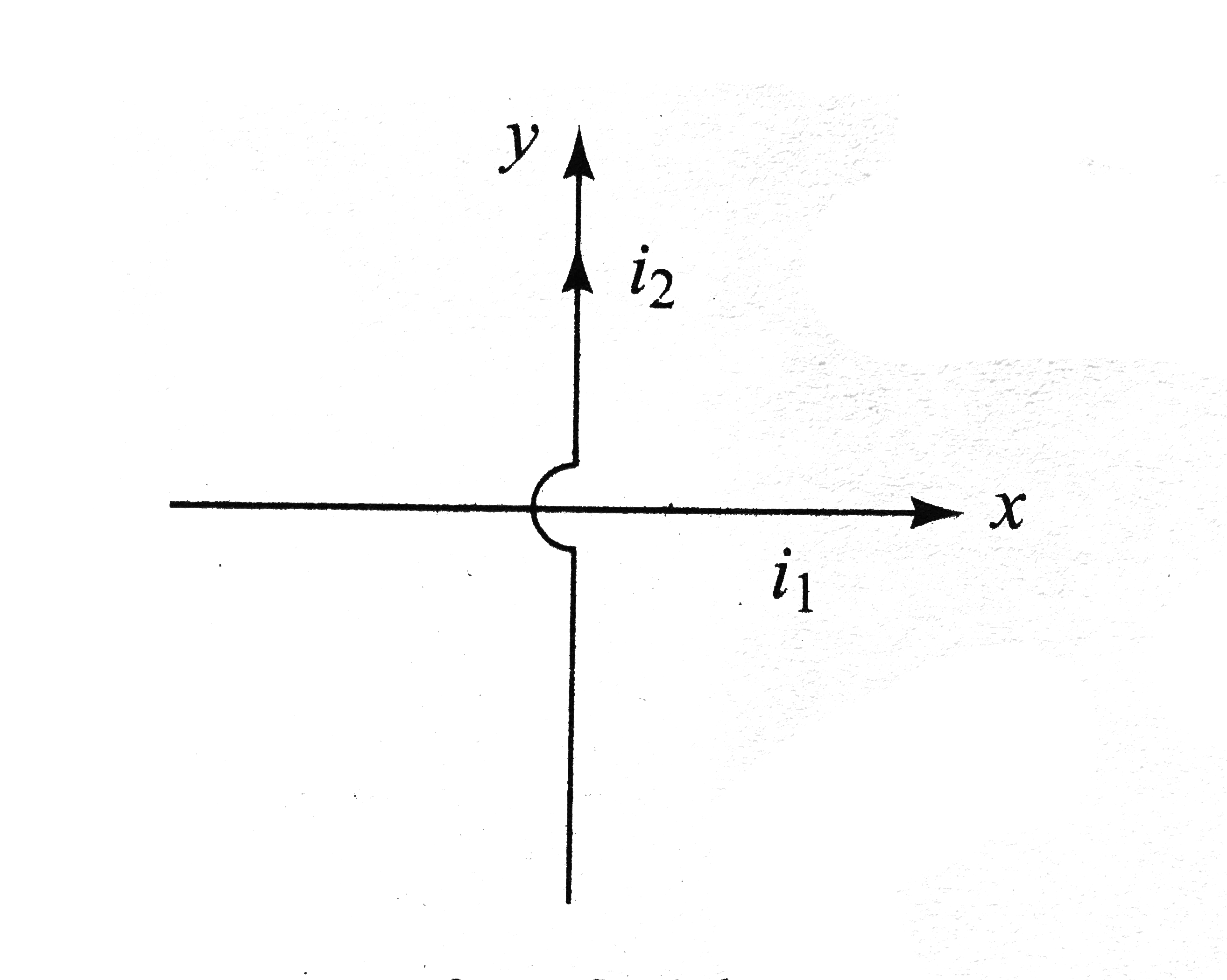
View SolutionThree coplanar parallel wires, each carrying a current of 10 A along the same direction, are placed with a separation 5.0 cm between the consecutive ones. Find the magnitude of the magnetic force per unit length acting on the wires.
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View SolutionA long straight wire is carrying current I in + z direction .The x-y plane contains a closed circular loop carrying current I2 and not encircling the straight wire.The force on the loop will be
View Solution
