The accelertion of a electron at a certain moment in a magnetic field B=2ˆi+3ˆj+4ˆk is a=xˆi+ˆj−ˆk. The value of x is
0.5
1
2.5
1.5
The correct Answer is:A
To solve the problem, we need to find the value of x in the acceleration vector a=x^i+^j−^k given that the magnetic field B=2^i+3^j+4^k.
1. Understanding the Relationship:
The force F on a charged particle moving in a magnetic field is given by the equation:
F=q(v×B)
where q is the charge of the particle, v is its velocity, and B is the magnetic field. The force F is always perpendicular to both v and B. Consequently, the acceleration a is also perpendicular to B.
2. Using the Perpendicular Condition:
Since a is perpendicular to B, we can use the dot product:
a⋅B=0
3. Substituting the Vectors:
Substitute a=x^i+^j−^k and B=2^i+3^j+4^k into the dot product:
(x^i+^j−^k)⋅(2^i+3^j+4^k)=0
4. Calculating the Dot Product:
Calculate the dot product:
=x⋅2+1⋅3+(−1)⋅4
This simplifies to:
2x+3−4=0
Therefore:
2x−1=0
5. Solving for x:
Rearranging gives:
2x=1⟹x=12
Final Answer:
The value of x is 0.5.
---
The force F on a charged particle moving in a magnetic field is given by the equation:
F=q(v×B)
where q is the charge of the particle, v is its velocity, and B is the magnetic field. The force F is always perpendicular to both v and B. Consequently, the acceleration a is also perpendicular to B.
Since a is perpendicular to B, we can use the dot product:
a⋅B=0
Substitute a=x^i+^j−^k and B=2^i+3^j+4^k into the dot product:
(x^i+^j−^k)⋅(2^i+3^j+4^k)=0
Calculate the dot product:
=x⋅2+1⋅3+(−1)⋅4
This simplifies to:
2x+3−4=0
Therefore:
2x−1=0
Rearranging gives:
2x=1⟹x=12
The value of x is 0.5.
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SCQ_TYPE
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
A charged particle has acceleration →a=2ˆi+xˆj in a magnetic field →B=−3ˆi+2ˆj−4ˆk.Find the value of x.
View SolutionIf →a=2ˆi−3ˆj−ˆk and →b=ˆi+4ˆj−2ˆk, then →a×→b is
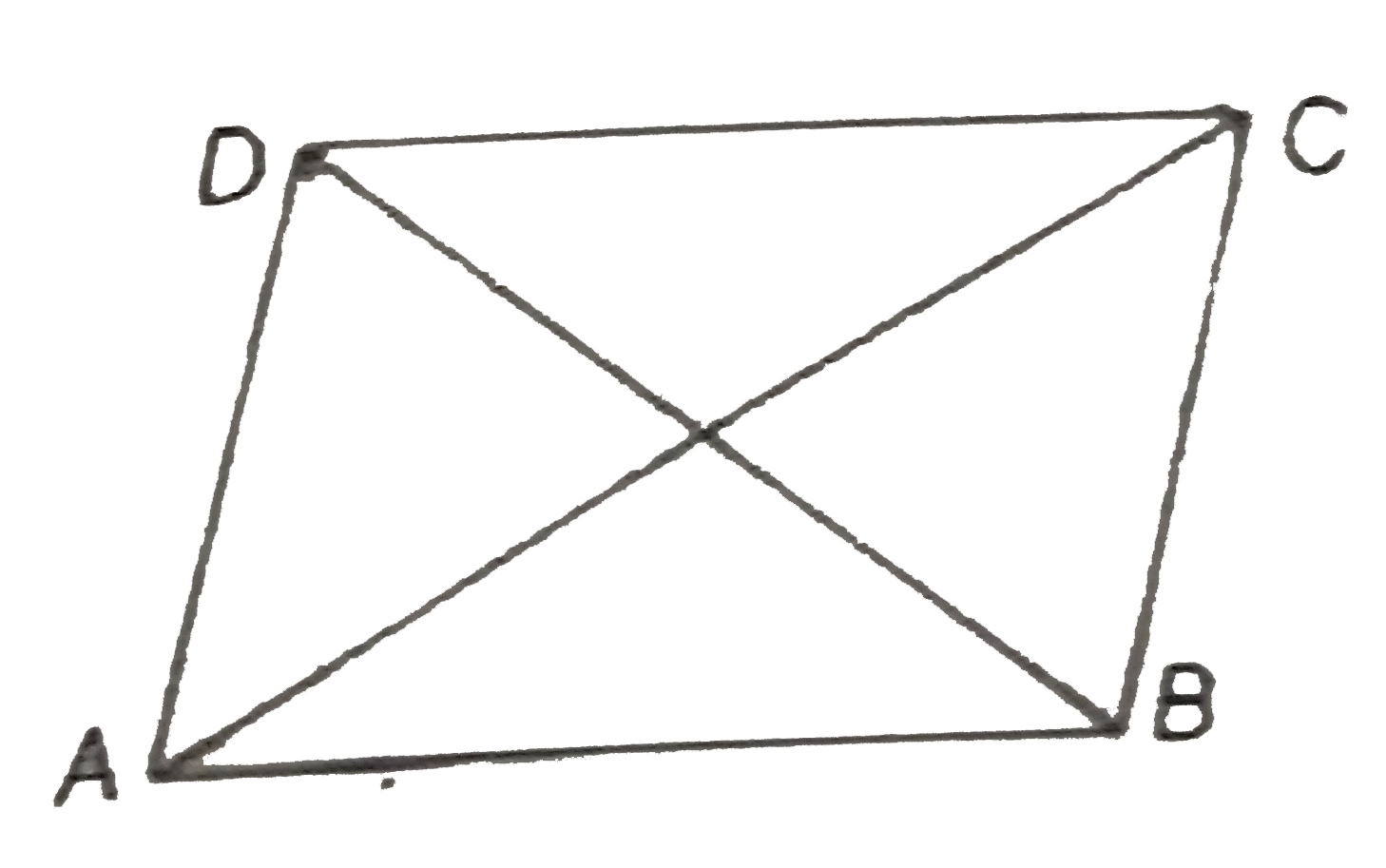
View SolutionIf in the shown figure AC=ˆi+2ˆj+4ˆk and BD=ˆi−3ˆj+ˆk then BC is
View SolutionIf →a=2ˆi−3ˆj−1ˆkand→b=ˆi+4ˆj−2ˆk then →a×→b is
View SolutionIf a=2ˆi+2ˆj−8ˆkandb=ˆi+3ˆj−4ˆk, then the magnitude of a+b is equal to
View SolutionIf →ω=2ˆi−3ˆj+4ˆk and →r=2ˆi−3ˆj+2ˆk then the linear velocity is
View SolutionShow that the vectors 2ˆi−3ˆj+4ˆk and −4ˆi+6ˆj−8ˆk are collinear.
View SolutionFind the angle between the vectors 4ˆi−2ˆj+4ˆkand3ˆi−6ˆj−2ˆk.
View SolutionIf a=2ˆi+3ˆj+4ˆkandb=4ˆi+3ˆj+2ˆk ,find the angel between a and b.
View SolutionThe vector equation of the plane containing he line →r=(−2ˆi−3ˆj+4ˆk)+λ(3ˆi−2ˆj−ˆk) and the point ˆi+2ˆj+3ˆk is
View Solution
