A solenoid has an inductance of 10H and a resistance of 2Ω. It is connected to a 10V battery. How long will it take for the magnetic energy to reach 1/4 of its maximum value?
To solve the problem step by step, we will follow the logical flow of the video transcript while ensuring clarity and completeness in the explanation.
Step 1: Identify Given Values
We have the following values from the problem:
- Inductance, L=10H
- Resistance, R=2Ω
- Voltage, V=10V
Step 2: Calculate Maximum Current
The maximum current I0 in the circuit can be calculated using Ohm's law:
I0=VR
Substituting the known values:
I0=10V2Ω=5A
Step 3: Determine Maximum Magnetic Energy
The maximum magnetic energy U stored in the solenoid can be calculated using the formula:
U=12LI20
Substituting L=10H and I0=5A:
U=12×10×(5)2=12×10×25=125J
Step 4: Calculate One-Fourth of Maximum Energy
We need to find the time when the magnetic energy reaches one-fourth of its maximum value:
U14=14U=14×125=31.25J
Step 5: Relate Current to Magnetic Energy
The magnetic energy U in terms of current I is given by:
U=12LI2
Setting this equal to 31.25J:
31.25=12×10×I2
Solving for I:
I2=31.25×210=6.25⟹I=√6.25=2.5A
Step 6: Use the Current Equation
The current I in an LR circuit as a function of time t is given by:
I=I0(1−e−RLt)
Substituting I=2.5A and I0=5A:
2.5=5(1−e−210t)
This simplifies to:
12=1−e−15t
Rearranging gives:
e−15t=12
Step 7: Solve for Time t
Taking the natural logarithm on both sides:
−15t=ln(12)
Thus:
t=−5ln(12)=5ln(2)
Using ln(2)≈0.693:
t≈5×0.693≈3.465s
Final Answer
The time taken for the magnetic energy to reach one-fourth of its maximum value is approximately:
t≈3.46s
We have the following values from the problem:
- Inductance, L=10H
- Resistance, R=2Ω
- Voltage, V=10V
The maximum current I0 in the circuit can be calculated using Ohm's law:
I0=VR
Substituting the known values:
I0=10V2Ω=5A
The maximum magnetic energy U stored in the solenoid can be calculated using the formula:
U=12LI20
Substituting L=10H and I0=5A:
U=12×10×(5)2=12×10×25=125J
We need to find the time when the magnetic energy reaches one-fourth of its maximum value:
U14=14U=14×125=31.25J
The magnetic energy U in terms of current I is given by:
U=12LI2
Setting this equal to 31.25J:
31.25=12×10×I2
Solving for I:
I2=31.25×210=6.25⟹I=√6.25=2.5A
The current I in an LR circuit as a function of time t is given by:
I=I0(1−e−RLt)
Substituting I=2.5A and I0=5A:
2.5=5(1−e−210t)
This simplifies to:
12=1−e−15t
Rearranging gives:
e−15t=12
Taking the natural logarithm on both sides:
−15t=ln(12)
Thus:
t=−5ln(12)=5ln(2)
Using ln(2)≈0.693:
t≈5×0.693≈3.465s
The time taken for the magnetic energy to reach one-fourth of its maximum value is approximately:
t≈3.46s
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 4
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 5
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 2
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A solenoid has an inductance of 50 mH and a resistance of 0.025Ω. If it is connected to a battery, how long will it take for the current to reach one half of its final equilibrium value?
View SolutionA solenoid of resistance 50Ω and inductance 80 H is connected to a 200 V battery, How long will it take for the current to reach 50% of its final equlibrium value ? Calculate the maximum enargy stored ?
View Solution
Knowledge Check
A solenoid has an inductance of 10 henty and a resistance of 2 ohm. It is connected to a 10 volt battery. How long will it take for the magnetic energy to reach 1/4 of its maximum value?
A3.5sB2.5sC5.5sD7.5s
A coil having an inductance L and a resistance R is connected to a battery of emfε. Find the time elapsed before, the magnetic field energy stored in the circuit reaches half its maximum value.
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
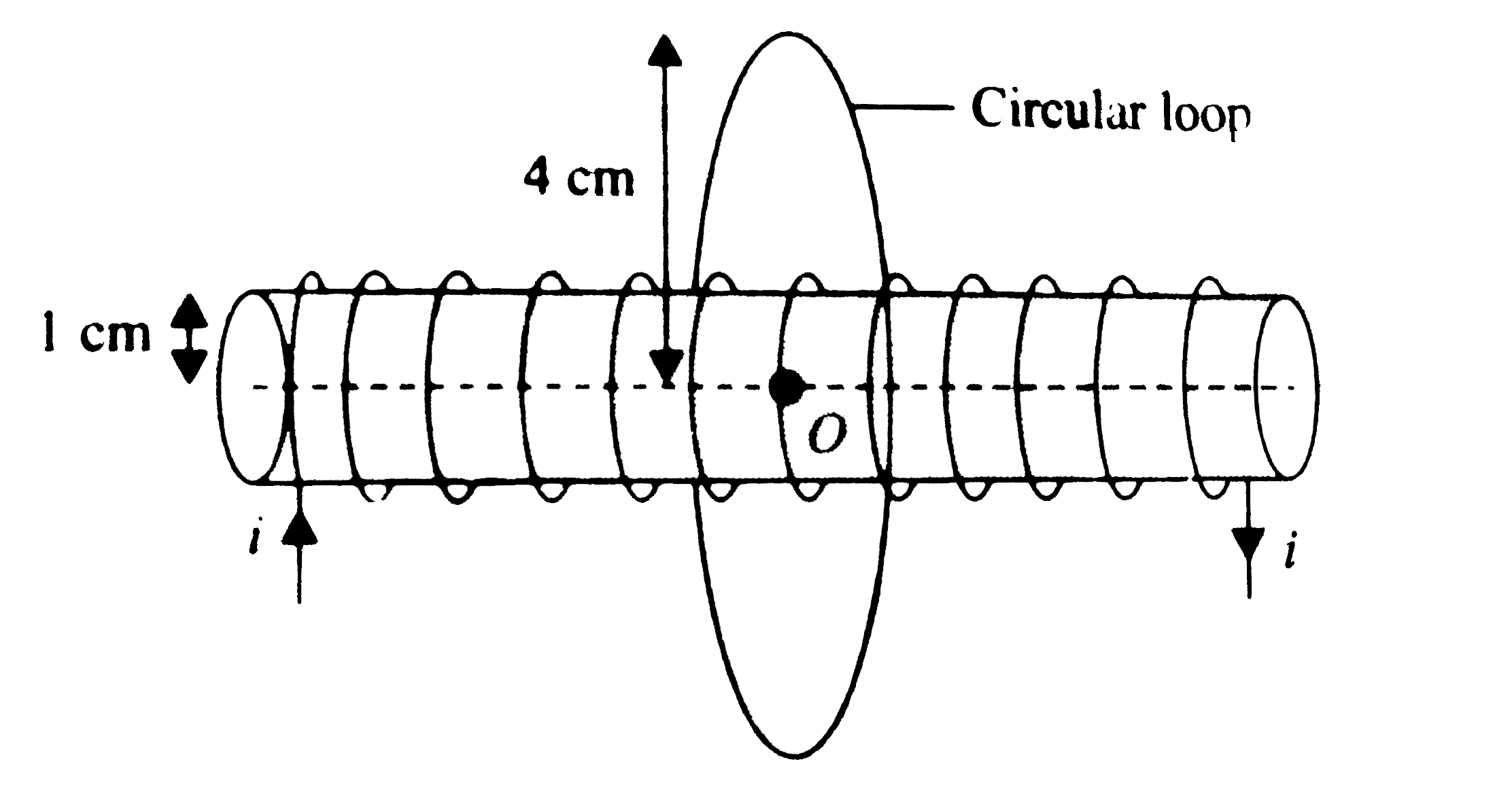
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionA solenoid of inductance 50 mH and resistance 10Ω is connected to a battery of 6V. Find the time elapsed before the current acquires half of its steady - state value.
View SolutionA coil of inductance 8.4mH and resistance 6 Ω is connected to a 12V battery. The current in the coil is 1.0A at approximately the time.
View SolutionA coil of inductance 8.4 mH and resistance 6(Ω) is connected to a 12 V battery. The current in the coil is 1.0 A at approximately the time
View SolutionA solenoid of inductance 50 mH and resistance 10 Omega is connected to a battery of 6V. Find the time elapsed before the current acquires half of its steady - stae value.
View SolutionAn inductor of 2 H and a resistance of 10Ω are connects in series with a battery of 5 V. The initial rate of change of current is
View Solution
