If is a capacitor C, then the constant accelerationn a of the wire.
To solve the problem, we need to find the constant acceleration a of a wire connected to a capacitor C in the presence of a magnetic field. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have a capacitor with capacitance C, and the wire is moving in a magnetic field B that is directed into the plane. The potential V across the capacitor can be expressed in terms of the charge Q and capacitance C.
Hint: Remember that the relationship between charge, capacitance, and potential is given by Q=CV.
Step 2: Calculate the Potential
According to Faraday's law of electromagnetic induction, the induced potential V can be expressed as:
V=LdΦdt
Where Φ is the magnetic flux. The induced emf V can also be expressed as:
V=L(v×B)
where v is the velocity of the wire.
Hint: The induced emf is related to the rate of change of magnetic flux through the loop formed by the wire.
Step 3: Determine the Charge on the Capacitor
The charge Q on the capacitor can be expressed as:
Q=CV=C(LvB)
This gives us:
Q=CLvB
Hint: The charge is directly proportional to both the capacitance and the induced emf.
Step 4: Relate Charge to Current
The current I flowing through the circuit can be defined as the rate of change of charge:
I=dQdt
Substituting for Q:
I=ddt(CLvB)
Assuming C, L, and B are constants, we have:
I=CLBdvdt
Hint: The current is related to how quickly the charge is changing with respect to time.
Step 5: Calculate the Magnetic Force
The magnetic force F acting on the wire can be expressed using the formula:
F=ILB
Substituting for I:
F=(CLBdvdt)LB=CB2L2dvdt
Hint: The magnetic force depends on the current, the length of the wire in the magnetic field, and the magnetic field strength.
Step 6: Apply Newton's Second Law
According to Newton's second law:
F=ma
where m is the mass of the wire. Therefore, we can write:
ma=CB2L2dvdt
Hint: The net force acting on the wire is equal to the mass times its acceleration.
Step 7: Solve for Acceleration
Rearranging the equation gives:
a=CB2L2m
Hint: This equation shows how the acceleration of the wire is influenced by the capacitance, magnetic field strength, and the mass of the wire.
Final Result
Thus, the constant acceleration a of the wire is given by:
a=CB2L2m
We have a capacitor with capacitance C, and the wire is moving in a magnetic field B that is directed into the plane. The potential V across the capacitor can be expressed in terms of the charge Q and capacitance C.
According to Faraday's law of electromagnetic induction, the induced potential V can be expressed as:
V=LdΦdt
Where Φ is the magnetic flux. The induced emf V can also be expressed as:
V=L(v×B)
where v is the velocity of the wire.
The charge Q on the capacitor can be expressed as:
Q=CV=C(LvB)
This gives us:
Q=CLvB
The current I flowing through the circuit can be defined as the rate of change of charge:
I=dQdt
Substituting for Q:
I=ddt(CLvB)
Assuming C, L, and B are constants, we have:
I=CLBdvdt
The magnetic force F acting on the wire can be expressed using the formula:
F=ILB
Substituting for I:
F=(CLBdvdt)LB=CB2L2dvdt
According to Newton's second law:
F=ma
where m is the mass of the wire. Therefore, we can write:
ma=CB2L2dvdt
Rearranging the equation gives:
a=CB2L2m
Thus, the constant acceleration a of the wire is given by:
a=CB2L2m
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Miscellaneous Examples
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.1
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 5
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A wire of mass m and length I can freely slide on a pair of parallel, smooth, horizontal rails placed in a vertical magnetic field B . The rails are connected by a capacitor of capacitance C. The electric resistance of the rails and the wire is zero. If a constant force F acts on the wire as shown in the figure, find the acceleration of the wire.
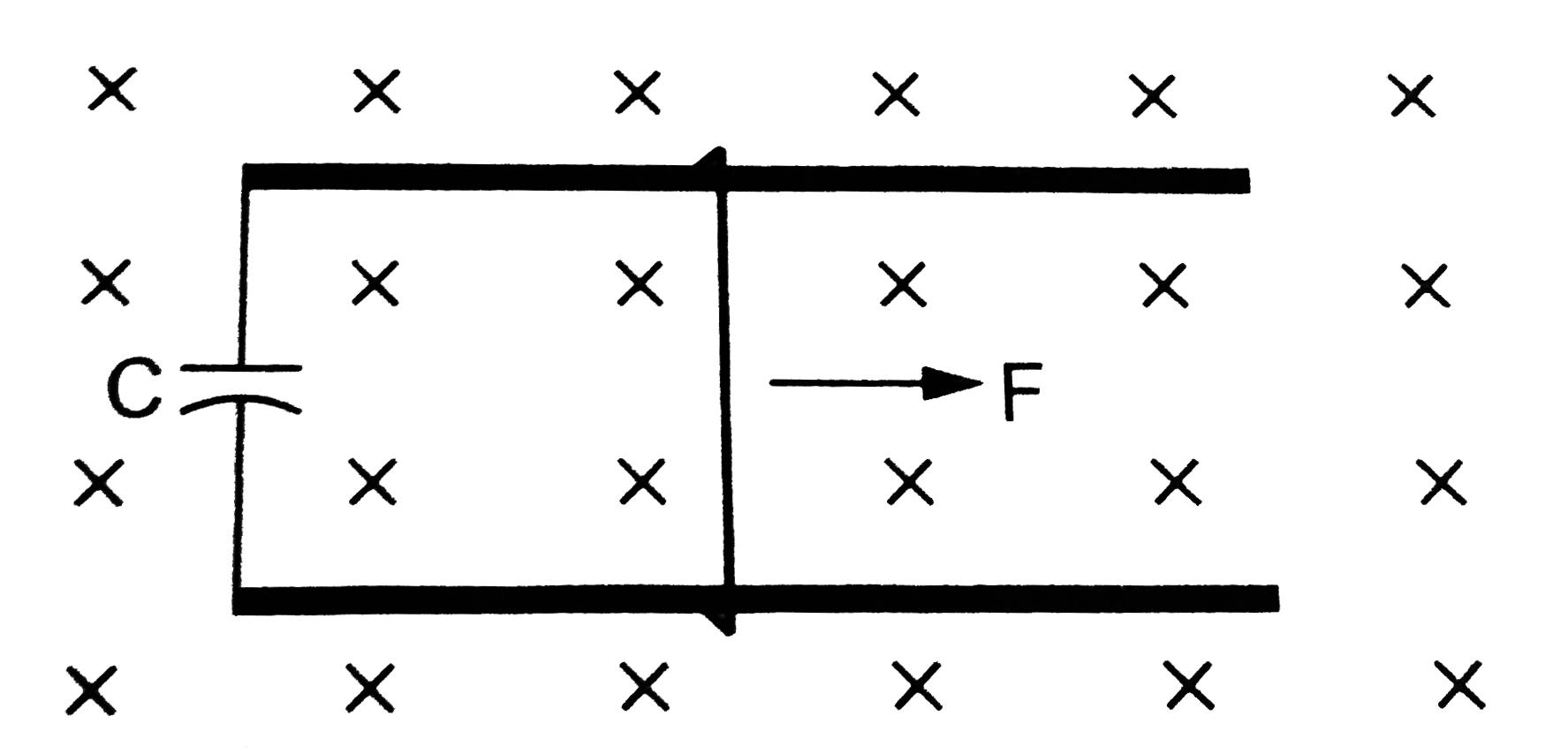
View SolutionA capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets
i. At the time of charging of capacitor time constant of the circuit is CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CR
View Solution
Knowledge Check
A wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAl
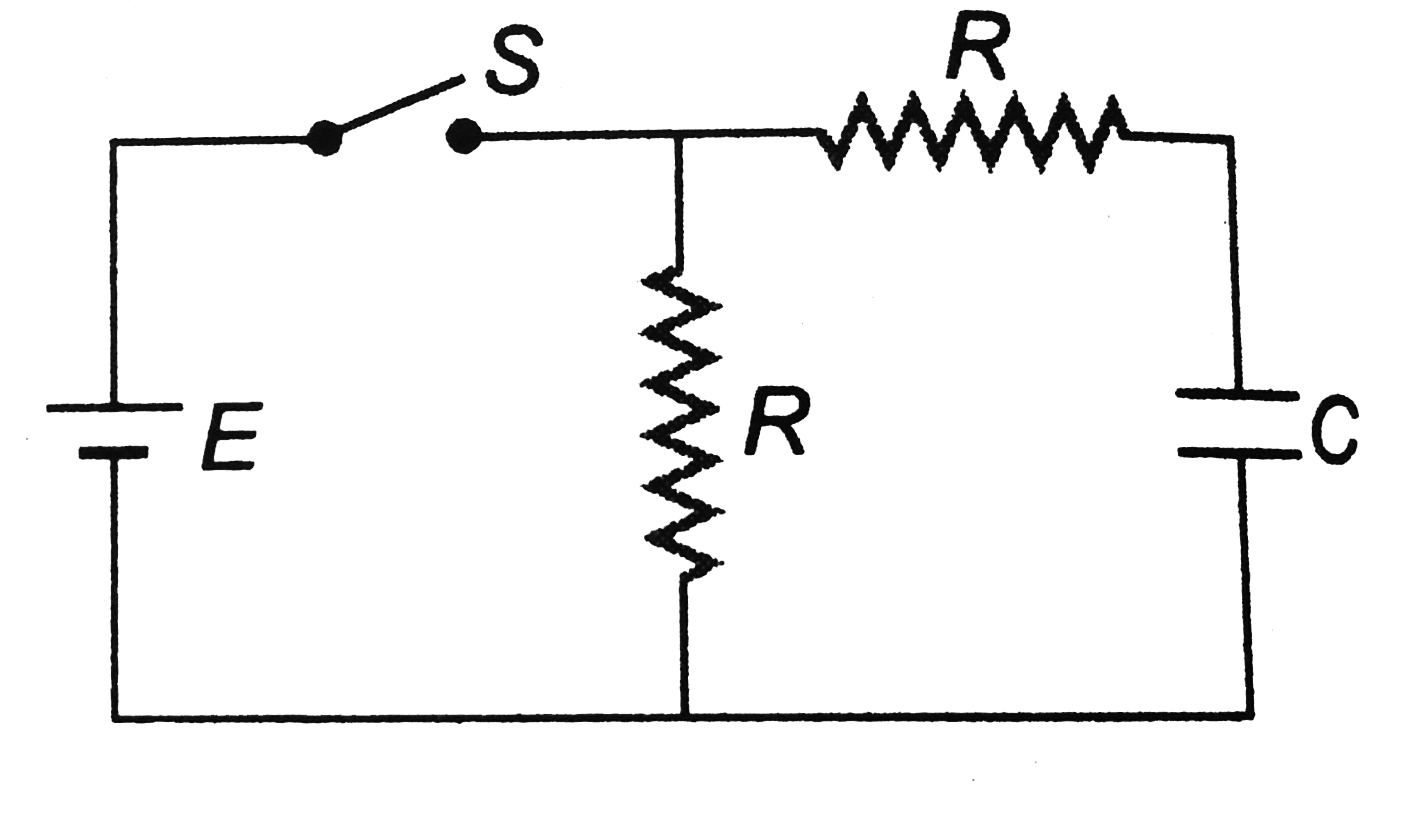
The time constant, for charging of capacitor C, when switch S is closed as shown in the figure , is
_PHY_E01_020_Q01.png)
View SolutionThe parallel combination of two air filled parallel plate capacitor of capacitance C and nC is connected to a battery of voltage, V. When the capacitors are fulley charged, the battery is removed and after that a dielectric material of dielectric constant K is placed between the two plates of the first capacitors. the new potential difference of the combined system is
View SolutionSTATEMENT-1: The capacitance of the capacitor remains constant irrespective of the charge present on it. because
STATEMENT-2: Capacitance depends on the size and the shape of the capacitor and also on the surrounding medium.
View SolutionStatement-1: If the plates of a capacitor are connected through a conducting wire, then its capacitance becomes infinite.
Statement-2: The capacitors cannot be charged.
View SolutionThe capacitance of a parallel plate capacitor is C when the region between the plate has air. This region is now filled with a dielectric slab of dielectric constant k. The capacitor is connected to a cell of emfE, and the slab is taken out
View SolutionA constant voltage is applied between the two ends of a metallic wire . If both the length and the radius of the wire are doubled , the rate of heat developed in the wire will
View SolutionTwo identical parallel plate capacitors are connected in series and then joined in series with a battery of 100V. A slab of dielectric constant K=3 is inserted between the plates of the first capacitor. Then, the potential difference across the capacitor will be, respectively.
View Solution
