For the situation described in figure, the magnetic field changes with time according to
B=(2.00t3−4.00t2+0.8)t and r2=2R=5.0cm

(a) Calculate the force on an electron located at P2 at t=2.00s
(b) What are the magnitude and direction of the electric field at P1 when t=3.00s and r1=0.02m.
a. At P2
El=dϕdt
E(2πr2)=πR2.dBdt
∴E=R22r2(dBdt)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Assertion And Reason10videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 1 Objective36videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 27.64videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A magentic field directed into the page changes with time according to B=(0.0300t2+1.4.40)T, where t is in seconds. The field has a circular cross section of radius R=2.50cm. What are the magitude and direction of the electric field at point P1 when t=3.00s and r1=0.0200m?
 View Solution
View SolutionThe position vector of a particle changes with time according to the direction →r(t)=15t2ˆi+(4−20t2)ˆj. What is the magnitude of the acceleration at t=1?
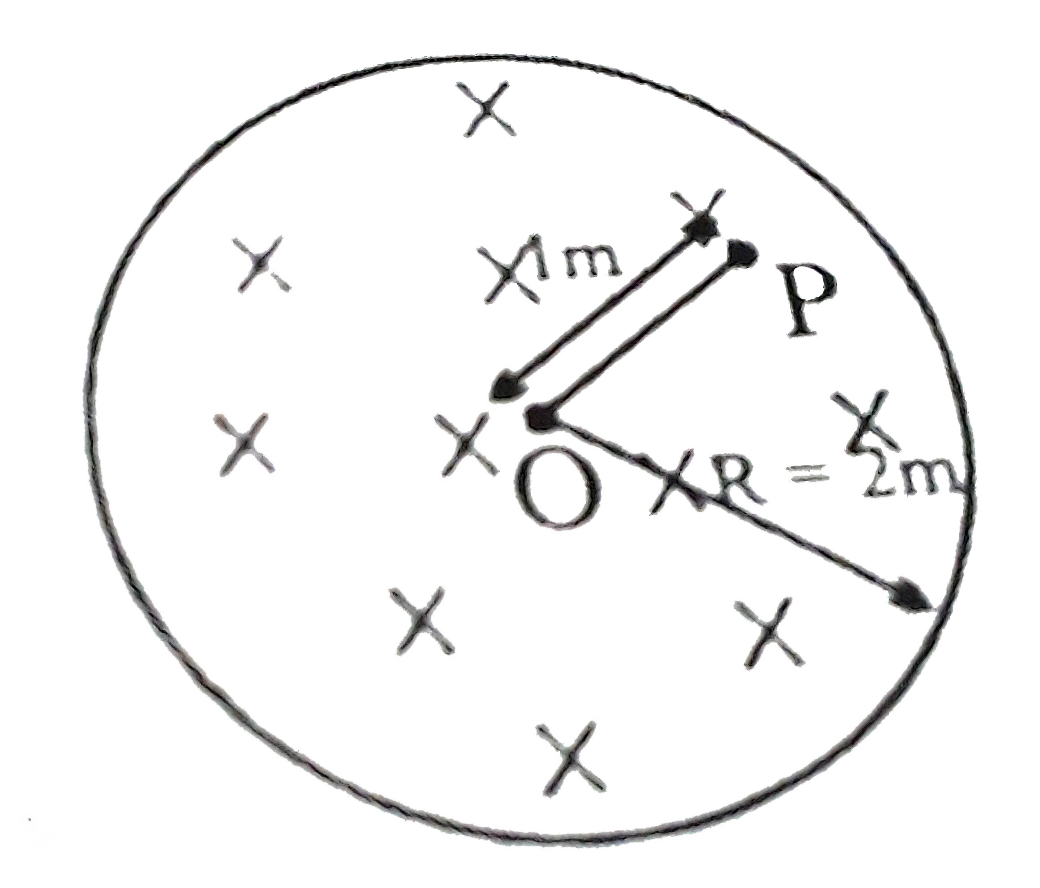
View SolutionA uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5 cm as shown in figure.

The force on an electron at P at t=2.0 s isView SolutionThe magnetic field in a certain cylindrical region is changing with time according to the law B=[16−4t2] Tesla . The magnitude of induced electric field at point P at time t= time =2 sec , is
 View Solution
View SolutionThe magnetic field perpendicular to the plane of a loop of area 0.1m2 is 0.2 T. Calculate the magnetic flux through the loop (in weber)
View SolutionA uniform magnetic field is restricted within a region of radius 1m. The magnetic field changes with time(t) as →B=B0(2t3)ˆk. A loop of radius 2m is outside the region of magnetic field as shown in figure. The emf induced in loop is
_PHY_E06_055_Q01.png) View Solution
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
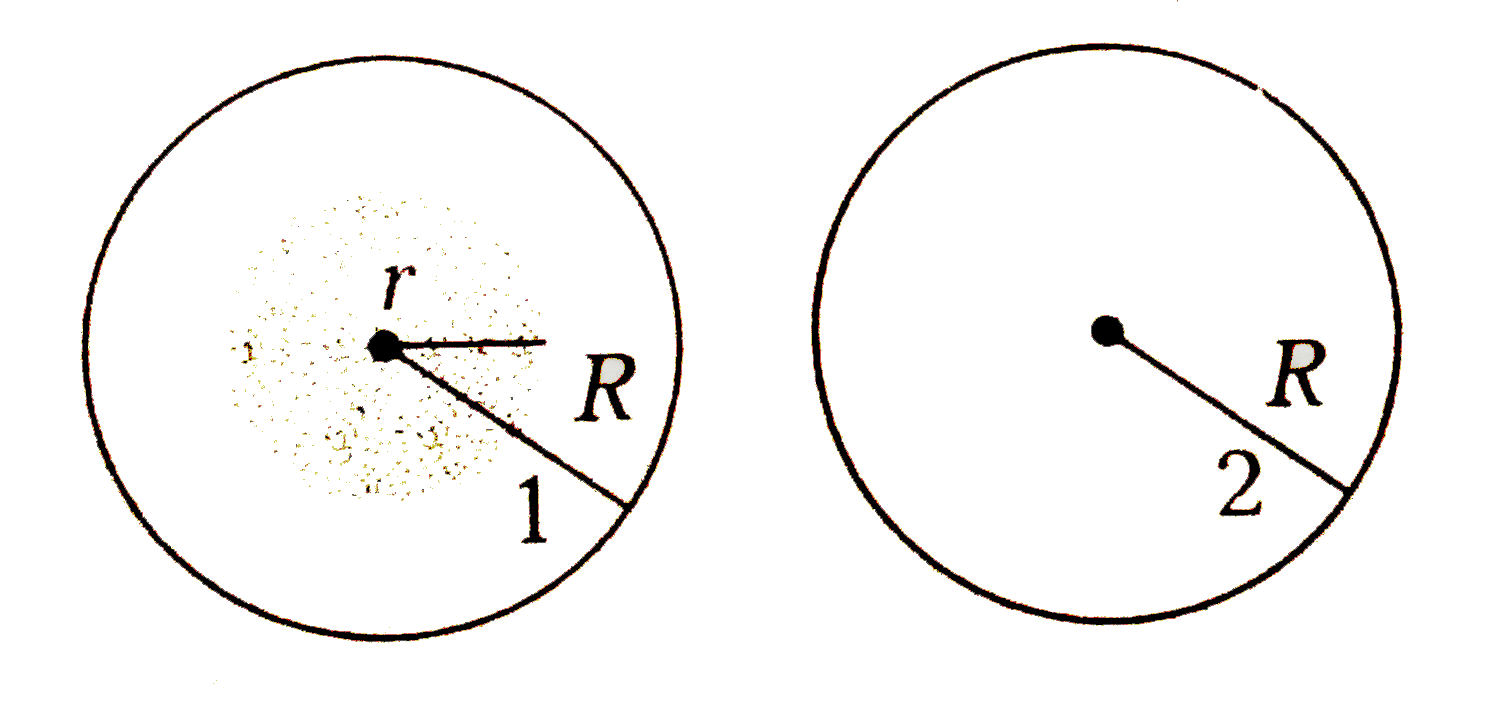
Zero in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and − d B d t π 2 in loop 2
− d B d t π R 2 in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and zero in loop 2View SolutionA stationary circular loop of radius a is located in a magnetic field which varies with time from t = 0 to t = T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
magnitude of charge flown through the loop from instant t = 0 to the instant when current reverses its direction.View SolutionA uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

In the previous problem, the direction of circular electric lines at t=1s isView SolutionThe position of a particle is given by r=3.0tˆi+2.0t2ˆj+5.0ˆk. Where t is in seconds and the coefficients hav the proper units for r to be in matres. (a) find v(t) and a(t) of the particle (b). Find the magnijtude of direction of v(t) or t=1.0 s
View Solution

