A particle moves perpendicular towards a plane mirror with a constant speed of 4cm/s.What is the speed of the image observed by an observed moving with 2cm/s along the same direction? Mirror is also moving with a speed of 10cm/s in the opposite direction.
(All speeds are with respect to ground frame of refrence)
4cm/s
12cm/s
14cm/s
26cm/s
The correct Answer is:D
To solve the problem step by step, we need to analyze the motion of the particle, the mirror, and the observer.
Step 1: Identify the speeds
- The speed of the particle moving towards the mirror, vp=4cm/s.
- The speed of the observer moving in the same direction as the particle, vo=2cm/s.
- The speed of the mirror moving in the opposite direction, vm=10cm/s.
Step 2: Determine the speed of the image with respect to the mirror
The speed of the image with respect to the mirror can be calculated using the formula:
vi/m=−vp+vm
Here, vp is positive as it is moving towards the mirror, and vm is negative because it is moving in the opposite direction.
Substituting the values:
vi/m=−4cm/s+10cm/s=6cm/s
This means the image moves at 6cm/s with respect to the mirror.
Step 3: Find the speed of the image with respect to the observer
Now, we need to find the speed of the image with respect to the observer. The formula is:
vi/o=vi/m−vo
Substituting the values we have:
vi/o=6cm/s−2cm/s=4cm/s
However, since the image is moving in the opposite direction to the observer, we need to consider the direction. Therefore, we can express this as:
vi/o=−4cm/s
Step 4: Final speed of the image
The speed of the image observed by the observer is 4cm/s in the leftward direction.
Summary
The speed of the image observed by the observer is 4cm/s towards the left.
---
- The speed of the particle moving towards the mirror, vp=4cm/s.
- The speed of the observer moving in the same direction as the particle, vo=2cm/s.
- The speed of the mirror moving in the opposite direction, vm=10cm/s.
The speed of the image with respect to the mirror can be calculated using the formula:
vi/m=−vp+vm
Here, vp is positive as it is moving towards the mirror, and vm is negative because it is moving in the opposite direction.
vi/m=−4cm/s+10cm/s=6cm/s
This means the image moves at 6cm/s with respect to the mirror.
Now, we need to find the speed of the image with respect to the observer. The formula is:
vi/o=vi/m−vo
Substituting the values we have:
vi/o=6cm/s−2cm/s=4cm/s
However, since the image is moving in the opposite direction to the observer, we need to consider the direction. Therefore, we can express this as:
vi/o=−4cm/s
The speed of the image observed by the observer is 4cm/s in the leftward direction.
The speed of the image observed by the observer is 4cm/s towards the left.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise Level 1 Subjective17videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 Single Correct16videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise Level 1 Assertion And Reason10videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary76videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Subjective21videos
REFRACTION OF LIGHT
Similar Questions
A man runs towards a mirror at a speed 15 m/s. The speed of the image relative to the man is
View SolutionAn object is moving towards a stationary plane mirror with a speed of 2 m/s. Velocity of the image w.r.t. the object is
View SolutionAn object is moving towards a moving mirror as shown in the figure. Find speed of image with respect to ground in m/sec.
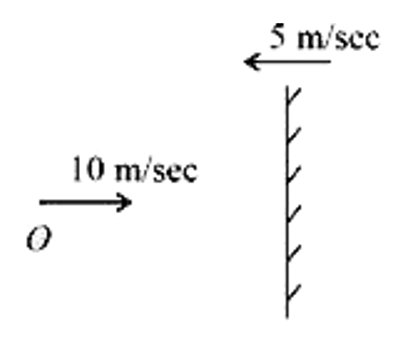 View Solution
View SolutionA man moving with 5ms−1 observes rain falling vertically at the rate of 10ms−1. Find the speed and direction of the rain with respect to ground.
View SolutionA particle moves in a straight line with constant speed of 4m/s for 2s, then with 6m/s for 3s. Find the average speed of the particle in the given time interval.
View SolutionA article moves in a circle of radius 20 cm with linear speed of 10 m/s. Find the angular velocity
View SolutionA particle moves towards a concave mirror of focal length 30cm along its axis and with a constant speed of 4cm/sec. At the instant the particle is 90cm from the pole
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View SolutionTwo particles of equal mass are moving along the same straight line with the same speed in opposite direction. What is the speed of the centre of mass of the system ?
View Solution
If an object moves towards a plane mirror with a speed v at an angle θ to the perpendicular to the plane of the mirror, find the relative velocity between the object and the image.View Solution

