A ray of light falls on a plane mirror. When the mirror is turned, about an axis at right angles to the plane of mirror by 20∘ the angle between the incident ray and new reflected ray is 45∘. The angle between the incident ray and original reflected ray was therefore.
(a) 35∘ or 50∘
(b) 25∘ or 65∘
(c) 45∘ or 5∘
(d) None of these
The correct Answer is:D
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the initial setup
When a ray of light strikes a plane mirror, it does so at a certain angle of incidence (I). According to the law of reflection, the angle of reflection (R) is equal to the angle of incidence. Thus, we have:
I=R
Step 2: Consider the rotation of the mirror
The problem states that the mirror is turned by 20∘ about an axis that is perpendicular to its plane. This means that the normal to the mirror surface also rotates by 20∘.
Step 3: Analyze the effect of the mirror's rotation
When the mirror is rotated by 20∘, the new angle of incidence (let's call it I′) will be the original angle of incidence (I) plus the angle of rotation:
I′=I+20∘
The angle of reflection will also change accordingly:
R′=I′=I+20∘
Step 4: Determine the relationship between the new reflected ray and the original reflected ray
According to the problem, the angle between the incident ray and the new reflected ray is 45∘. This means:
I′+R′=45∘
Since R′=I+20∘, we can substitute this into the equation:
I+20∘+I+20∘=45∘
2I+40∘=45∘
Step 5: Solve for the original angle of incidence
Now, we can solve for I:
2I=45∘−40∘
2I=5∘
I=5∘2=2.5∘
Step 6: Find the angle between the incident ray and the original reflected ray
Since the angle of reflection R is equal to the angle of incidence I:
R=I=2.5∘
The angle between the incident ray and the original reflected ray is:
I+R=2.5∘+2.5∘=5∘
Final Answer
The angle between the incident ray and the original reflected ray is 5∘.
---
When a ray of light strikes a plane mirror, it does so at a certain angle of incidence (I). According to the law of reflection, the angle of reflection (R) is equal to the angle of incidence. Thus, we have:
I=R
The problem states that the mirror is turned by 20∘ about an axis that is perpendicular to its plane. This means that the normal to the mirror surface also rotates by 20∘.
When the mirror is rotated by 20∘, the new angle of incidence (let's call it I′) will be the original angle of incidence (I) plus the angle of rotation:
I′=I+20∘
R′=I′=I+20∘
According to the problem, the angle between the incident ray and the new reflected ray is 45∘. This means:
I′+R′=45∘
I+20∘+I+20∘=45∘
2I+40∘=45∘
Now, we can solve for I:
2I=45∘−40∘
2I=5∘
I=5∘2=2.5∘
Since the angle of reflection R is equal to the angle of incidence I:
R=I=2.5∘
I+R=2.5∘+2.5∘=5∘
The angle between the incident ray and the original reflected ray is 5∘.
Topper's Solved these Questions
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 More Than One Correct
6 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Level 2 Comprehensive Based
4 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Exercise Level 1 Subjective
17 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Subjective
21 Videos
Similar Questions
Knowledge Check
The angle of incidence on a plane mirror is 30∘ . The angle between the incident ray and the reflected ray is
A30∘B15∘C60∘D90∘The angle between the incident ray and the ray reflected from the plane mirror is 70∘. The angle of incidence will be:
A70∘B30∘C35∘D90∘
In the figure given the angle between incident ray and the reflected ray is 70∘

Find the angle between the mirror and the incident ray.
View SolutionThe angle between the incident ray and the refracted ray of a prism is called angle of deviation.
View SolutionA ray of light falls normally on a plane mirror. What is the angle of incidence ?
View SolutionIn the figure given the angle between incident ray and the reflected ray is 70∘
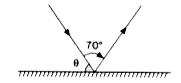
Find the angle of incidence.
View SolutionIf the angle of incidence is 32∘, then what will the angle between incident ray and reflected ray?
View SolutionIn the figure given the angle between incident ray and the reflected ray is 70∘
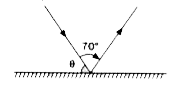
Find the angle of reflection.
View Solution