The prism shown in figure has a refractive index of 1.60 and the angles A are 30∘. Two light rays P and Q are parallel as they enter the prism. What is the angle between them after they emerge? [sin−1(0.8)=53∘]
![The prism shown in figure has a refractive index of 1.60 and the angles A are 30^@. Two light rays P and Q are parallel as they enter the prism. What is the angle between them after they emerge? [sin^-1(0.8)=53^@]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V05_C31_E01_029_Q01.png)
15∘
30∘
45∘
60∘
The correct Answer is:B
μ=(sinisin45∘) or √32=sini(1/√2) or i=60∘
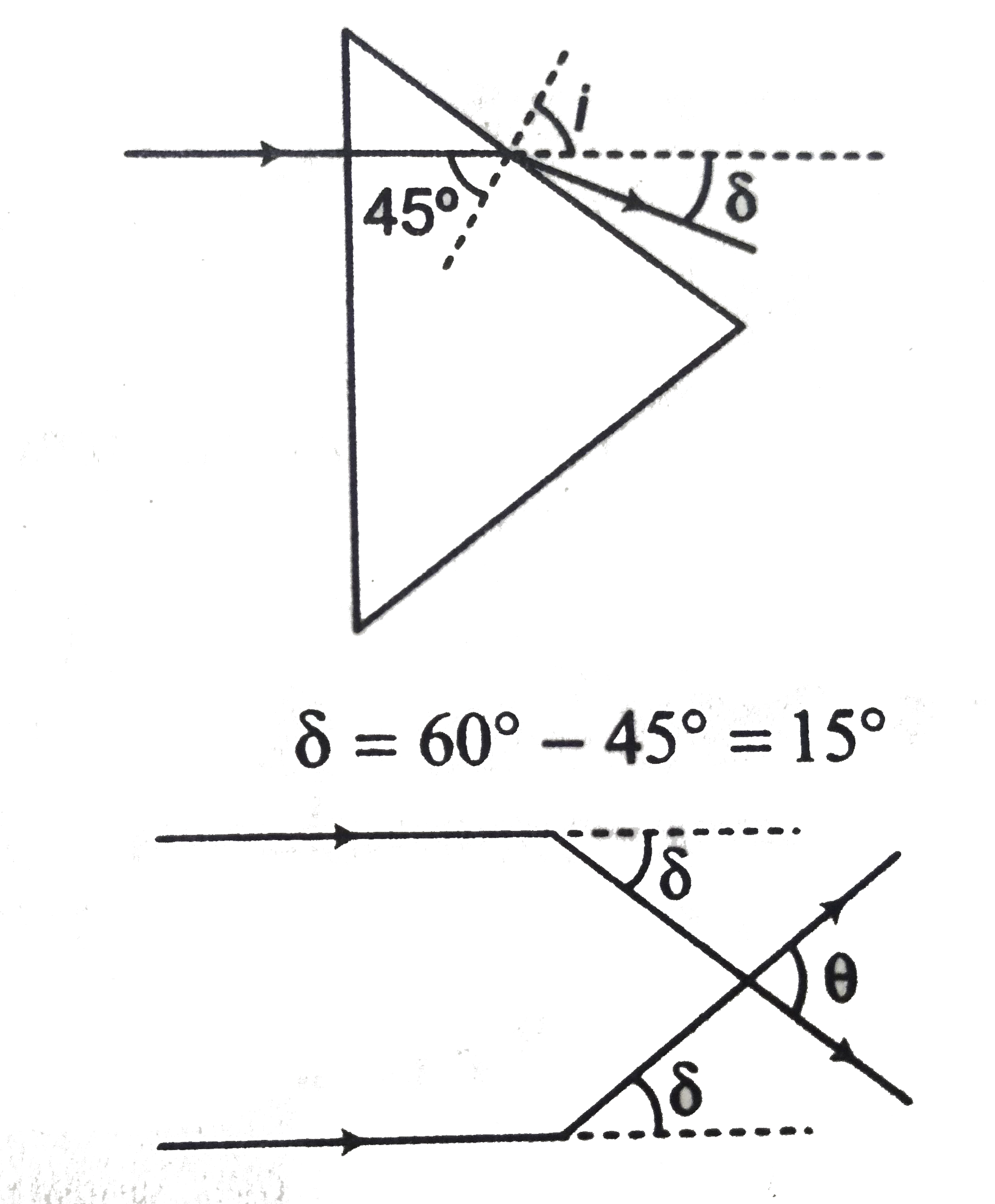
∴δ=60∘−45∘=15∘

θ=2δ=30∘
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions1videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Subjective29videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 1 Assertion And Reason13videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
For a prism of refractive index 1.732, the angle of minimum deviation is equal to the angle of the prism. The angle of the prism is
View Solution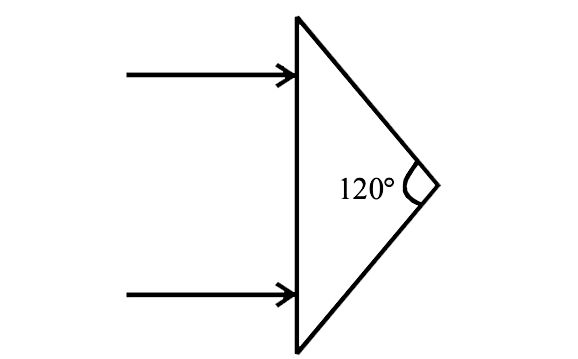
An isosceles prism of angle 120degree has a refractive index 1.44. Two parallel monochromatic rays enter the prism parallel to each other in air as shown. The rays emerge from the opposite facesView SolutionA glass prism has a refractive angle of 90∘ and a refractive index of 1.5. A ray is incident at an angle of 30∘. The ray emerges from an adjacent face at an angle of
View SolutionIf a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
View SolutionIf a light ray incidents normally on one of the faces of the prism of refractive index 2 and the emergent ray just grazes the second face of the prism, then the angle of deviation is
View SolutionWhat is the angle of incidence for an equilateral prism of refractive index √3 so that the ray si parallel to the base inside the prism?
View SolutionA ray of light is incident on a prism whose refractive index is 1.52 at an angle of 40∘. If the angle of emergence is 60∘, calculate the angle of the prism.
View SolutionRefractive index of a prism is √7/3 and the angle of prism is 60∘. The minimum angle of incidence of a ray that will be transmitted through the prism is
View SolutionRefractive index of a prism is √73 and the angle of prism is 60∘. The limiting angle of incidence of a ray that will be transmitted through the prism is approximately
View SolutionA prism of refractive index 1.53 is placed in water of refractive index 1.33. If the angle of prism is 60∘, calculate the angle of minimum deviation in water.
View Solution

