A beam of light parallel to central line AB is incident on the plane of slits. The number of minimum, obtained on the large screen is n1. Now if the beam is tilted by some angle (≠90∘) as shown in figure, then the number of minima obtained is n2. Then, 
n1=n2
n1>n2
n2>n1
n2 will be zero.
The correct Answer is:A
Only fringe pattern will shift. Number of fringes
on screen will remain unchanged.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1Subjective22videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Subjective Questions5videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 1 Objective11videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
Similar Questions
In figure, if a parallel beam of white light is incident on the plane of the slit, then the distance of the nearest white spot on the screen form O is [assume d<<D,λ<<D]
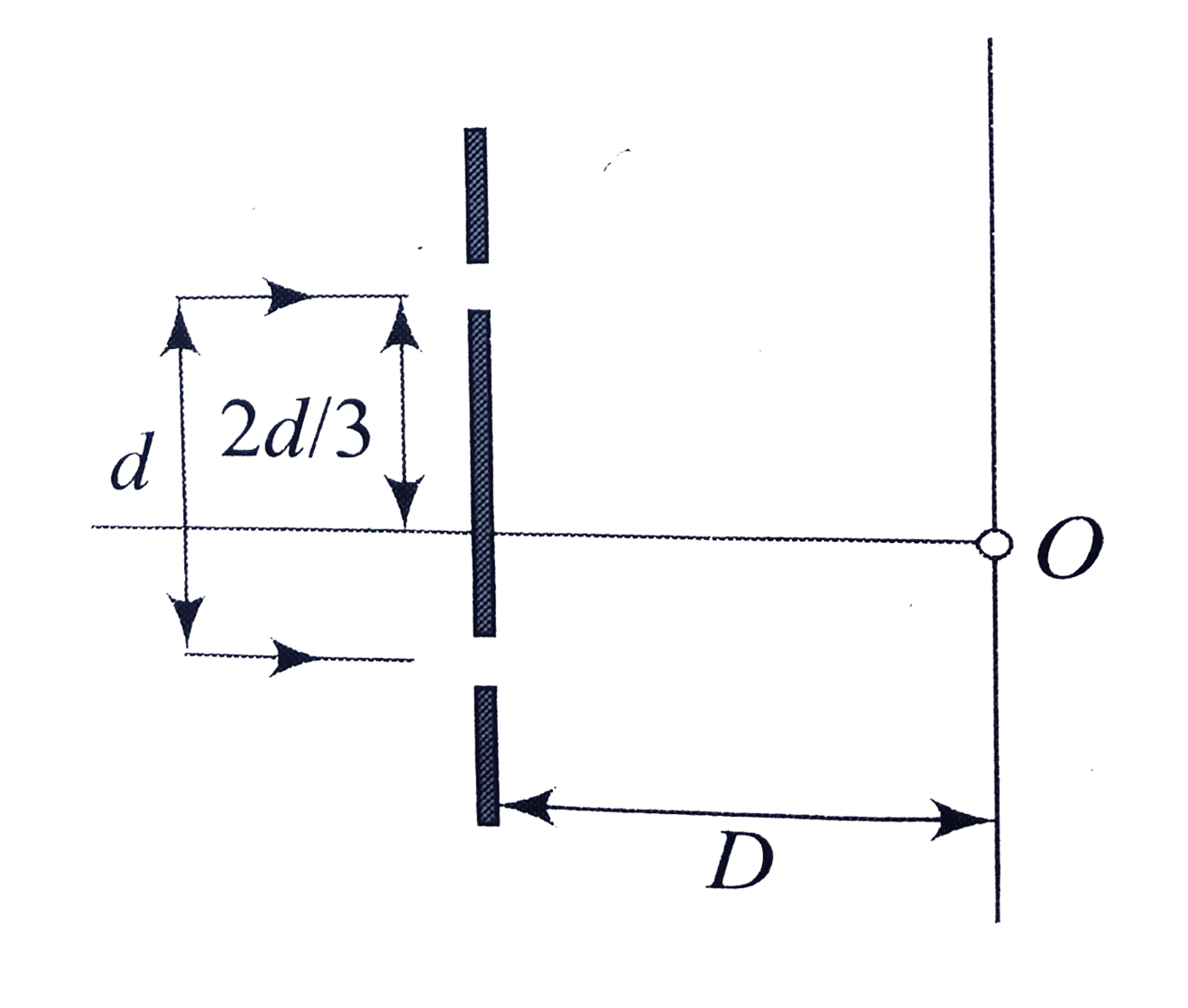View SolutionLight of wavelength 5000 Å is incident on a slit of width 0.1 mm. Find out the width of the central bright line on a screen distance 2m from the slit?
View Solution
Knowledge Check
- Question 1 - Select One
A parallel beam of light of wavelength 600 nm is incident normally on a slit of width d. If the distance between the slits and the screen is 0.8 m and the distance of 2nd order maximum from the centre of the screen is 15 mm. The width of the slit is
A40μmB80μmC160μmD200μm
In the figure , if a parallel beam of white light is incident on the plane of the slits S1andS2 then the distance of the nearest white spot on the screen from O is [ Assume D>>d,d>>λ ]
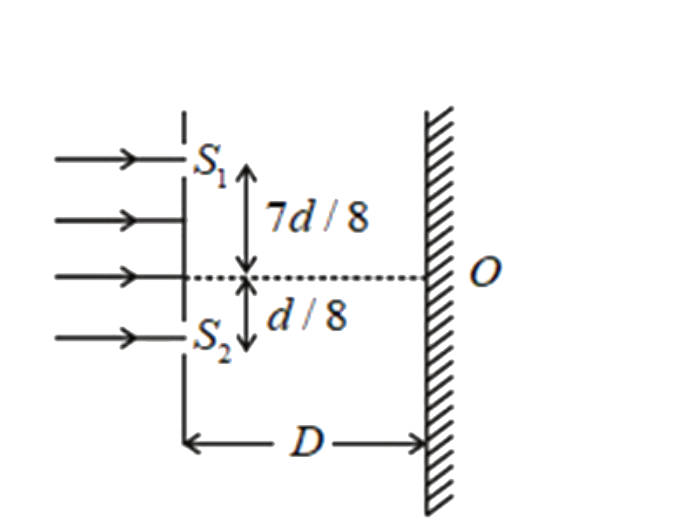View SolutionA coherent parallel beam of light of wavelength 5000A is incident normally on the plane of slits. The slit S1 is covered with a slab of refractive index μs=1.5 and thickness t=4×10−5m as shown. The separation between the slits is d=1mm and the separtion between the plane of slits and screen is D=1m. Then the position of the central maxima formed on the screen is
View SolutionIn Young's double slit experiment parallel monochromatic light is incident on both the slits at an angle as shown in the figure. To obtain the central maxima at on the screen we can
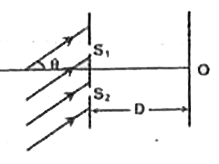View SolutionLight of wavelength 6000A0 is incident on a single slit. The first minimum of the diffraction pattern is obtained at 4 mm from the centre. The screen is at a distance of 2m from the slit. The slit width will be
View SolutionA coherent parallel beam of microwaves of wavelength λ=0.5mm falls on aYoung's double- slit apparatus. The separation between the slits is 1.0 mm. The intensity of microwaves is measured on a screen placed parallel to the plane of the slits at a distance of 1.0 m from it as shown in Fig. 2.42.
If the incident beam makes an angle or 30∘ with the x-axis (as in the dotted arrow shown in the figure), find the y-coordinates of the first minima on either side of the central maximum.
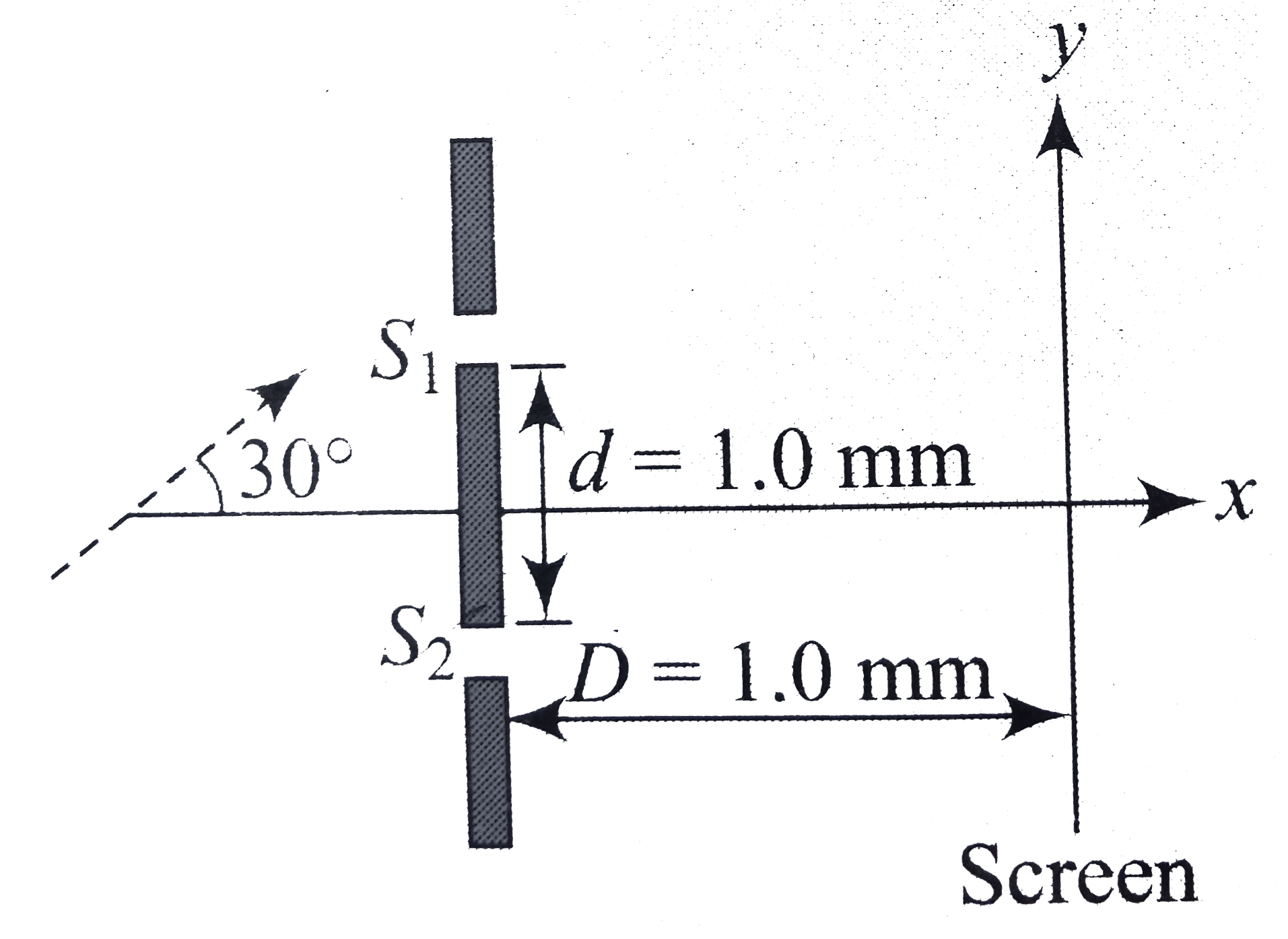View SolutionA monochromatic light of wavelength 500nm is incident normally on a single slit of width 0.2 nm of produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experimental with fringe width 0.5mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.View SolutionIn figure, parallel beam of light is incident on the plane of the slits of a Young's double-slit experiment. Light incident on the slit S1 passes through a medium of variable refractive index μ=1+ax (where 'x' is the distance from the plane of slits as shown), up to distance 'I' before falling on S1. Rest of the space is filled with air. If at 'O' a minima is formed. then the minimum value of the positive constant a (in terms of l and wavelength λ in air) is
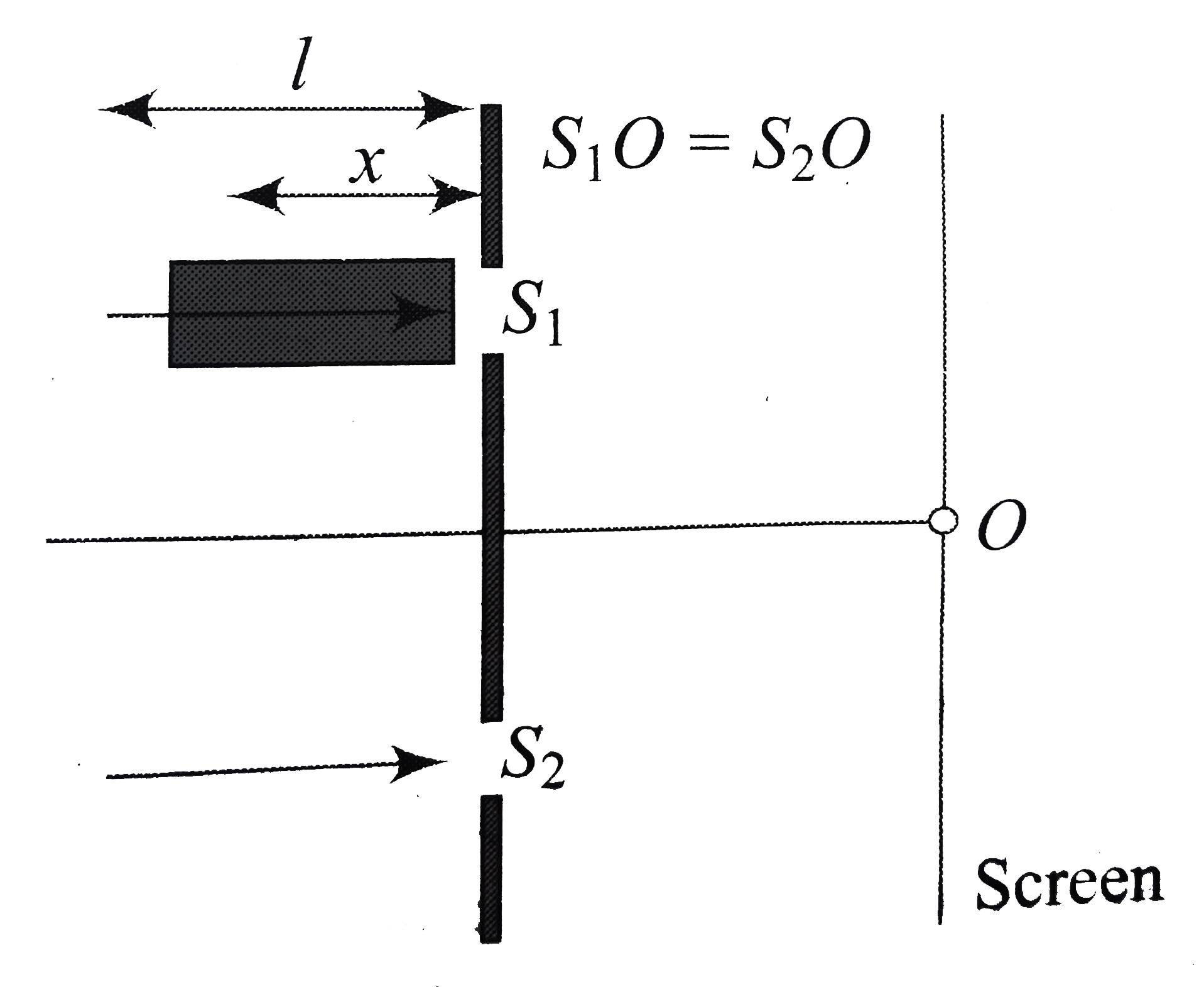View Solution