A double slit of separation 0.1 mm is illuminated by white light. A coloured interference pattern is formed on a screen 100 cm away. If a pin hole is located in this screen at a distance of 2 mm from the central fringe, the wavelength in the visible spectrum (4000 Å to 7000Å) which will be absent in the light transmitted through the pin hole is (are)
4000 Å
5000Å
6000Å
7000Å
The correct Answer is:A
To solve the problem step by step, we need to determine the wavelengths of light that will be absent in the light transmitted through the pinhole located at a distance of 2 mm from the central fringe in a double-slit interference pattern.
1. Understand the Condition for Destructive Interference:
Destructive interference occurs when the path difference between the light waves from the two slits is an odd multiple of half the wavelength. The condition for destructive interference is given by:
Δy=(2n−1)λDd
where:
- Δy is the distance from the central maximum to the point of interest (2 mm in this case),
- D is the distance from the slits to the screen (100 cm or 1 m),
- d is the distance between the slits (0.1 mm or 0.1×10−3 m),
- n is an integer (1, 2, 3,...).
2. Convert Units:
Convert all measurements to meters for consistency:
- Δy=2 mm=2×10−3 m
- d=0.1 mm=0.1×10−3 m
- D=100 cm=1 m
3. Substitute Values into the Destructive Interference Condition:
Rearranging the equation for λ:
λ=(2n−1)ΔydD
Substitute the known values:
λ=(2n−1)(2×10−3)(0.1×10−3)1
Simplifying this gives:
λ=(2n−1)×2×10−7 m
4. Convert Wavelength to Angstroms:
Since 1 m=1010 Å:
λ=(2n−1)×2×10−7×1010 Å=(2n−1)×2000 Å
5. Calculate Wavelengths for Different Values of n:
- For n=1:
λ=(2×1−1)×2000=2000 Å
- For n=2:
λ=(2×2−1)×2000=6000 Å
- For n=3:
λ=(2×3−1)×2000=10000 Å(not in visible range)
6. Identify Wavelengths in the Visible Spectrum:
The visible spectrum ranges from 4000 Å to 7000 Å. The wavelengths calculated that fall within this range are:
- 2000 Å (not visible)
- 6000 Å (visible)
7. Conclusion:
The wavelength that will be absent in the light transmitted through the pinhole is 6000 Å.
Destructive interference occurs when the path difference between the light waves from the two slits is an odd multiple of half the wavelength. The condition for destructive interference is given by:
Δy=(2n−1)λDd
where:
- Δy is the distance from the central maximum to the point of interest (2 mm in this case),
- D is the distance from the slits to the screen (100 cm or 1 m),
- d is the distance between the slits (0.1 mm or 0.1×10−3 m),
- n is an integer (1, 2, 3,...).
Convert all measurements to meters for consistency:
- Δy=2 mm=2×10−3 m
- d=0.1 mm=0.1×10−3 m
- D=100 cm=1 m
Rearranging the equation for λ:
λ=(2n−1)ΔydD
Substitute the known values:
λ=(2n−1)(2×10−3)(0.1×10−3)1
Simplifying this gives:
λ=(2n−1)×2×10−7 m
Since 1 m=1010 Å:
λ=(2n−1)×2×10−7×1010 Å=(2n−1)×2000 Å
- For n=1:
λ=(2×1−1)×2000=2000 Å
- For n=2:
λ=(2×2−1)×2000=6000 Å
- For n=3:
λ=(2×3−1)×2000=10000 Å(not in visible range)
The visible spectrum ranges from 4000 Å to 7000 Å. The wavelengths calculated that fall within this range are:
- 2000 Å (not visible)
- 6000 Å (visible)
The wavelength that will be absent in the light transmitted through the pinhole is 6000 Å.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - LEVEL 2 (single correct option)1videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 More Than One Correct6videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Subjective Questions5videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
Similar Questions
A double slit of separation 1.5 mm is illuminated by white light (between 4000 and 8000 Å). On a screen 120 cm away colored interference pattern is formed. If a pinhole is made on this screen at a distance of 3.0 mm from the central white fringe, some wavelengths will be absent in the transimitted light. Find the second longest wavelength (in Å) which will be absent in the transmitted light.
View SolutionA double slilt experiment is performed with sodium (yellow) light of wavelength 589.3 nm and the interference pattern is observed on a screen 100 cm away. The tenth bright fringe has its centre at a distance of 12 mm from the central maximum. Find the separation betwen the slits.
View Solution
Knowledge Check
- Question 1 - Select One
In Young's double-slit experiment, the slit are 0.5 mm apart and the interference is observed on a screen at a distance of 100 cm from the slits, It is found that the ninth bright fringe is at a distance of 7.5 mm from the second dark fringe from the center of the fringe pattern. The wavelength of the light used in nm is
A25007B2500C5000D50007
A single slit of width 0.1mm is illuminated by parallel light of wavelength 6000Å, and diffraction bands are observed on a screen 40cm from the slit. The distance of third dark band from the central bright band is:
View SolutionIn Young's experiment the slits, separated by d=0.8mm, are illuminated with light of wavelength 7200 Å, Interference pattern is obtained on a screen D=2m from the slits. Find minimum distance from central maximum at which the a average intensity is 50% if of maximum?
View SolutionWith two slits spaced 0.2 mm apart and a screen at a distance of 1 m, the third bright fringe is found to be at 7.5 mm from the central fringe. The wavelength of light used is
View SolutionA single slit of width 0.1 mm is illuminated by a parallel beam of light of wavelength 6000Å and diffraction bands are observed on a screen 0.5 m from the slit. The distance of the third dark band from the central bright band is _______ mm.
View SolutionA single slit of width 0.1 mm is illuminated by a parallel beam of light of wavelength 6000Å and diffraction bands are observed on a screen 0.5 m from the slit. The distance of the third dark band from the central bright band is _______ mm.
View SolutionWhite light is passed through a double slit and interference pattern is observed on a screen 2.5 m away. The separation between the slits is 0.5 mm. The first violet and red fringes are formed 2.0 mm and 3.5 mm away from the central white fringe. Calculate the wavelengths of the violet and the red light.
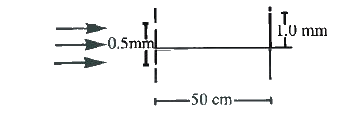
View SolutionWhite coheral light (400 nm 700 nm ) is sent through the slit of a Young.s double slit experiment. The separation between the slits is 0.5 mm and the screen is 50 away from the slits . There is a hole in the screen at a point 1.0 mm away (along the width of the fringes) from the central line. Which wavelengths (s) will be absent in the light coming from the hole ?
 View Solution
View Solution

