A parallel beam of light (λ=5000Å) is incident at an angle θ=30∘ with the normal to the slit plane in a Young's double slit experiment. The intensity due to each slit is I0. Point O is equidistant from S1andS2. The distance between slits is 1mm. 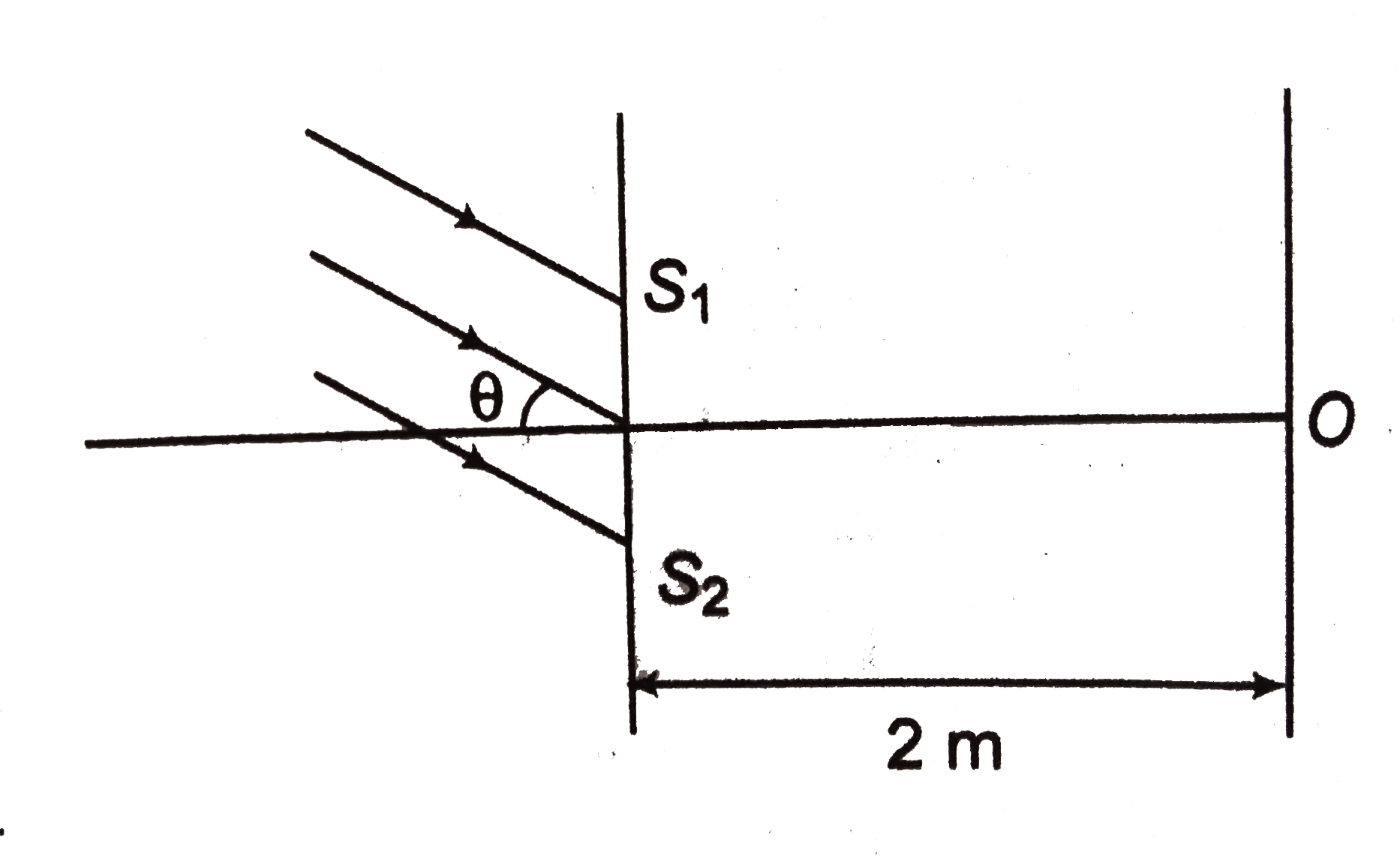
the intensity at P is 4I0.
The intensity at O is zero.
The intensity at a point on the screen 4mm above O is 4I0.
The intensity at a point on the screen 4 mm above O is zero.
The correct Answer is:A, C
Δx0=dsinθ=(10−3)(12)
=5×10−4m=(103)λ
Since, Δx0 is integer multiple of λ, it will produce
maximum intensity or 4I0 at O.
ω=λDd=(5×10−7)(2)10−3
=10−3m=1mm
At 4 mm, we will get 4th order maxima.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Comprehensionn Based4videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective5videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - LEVEL 2 (single correct option)1videos
INTERFERENCE AND DIFFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions135videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
Similar Questions
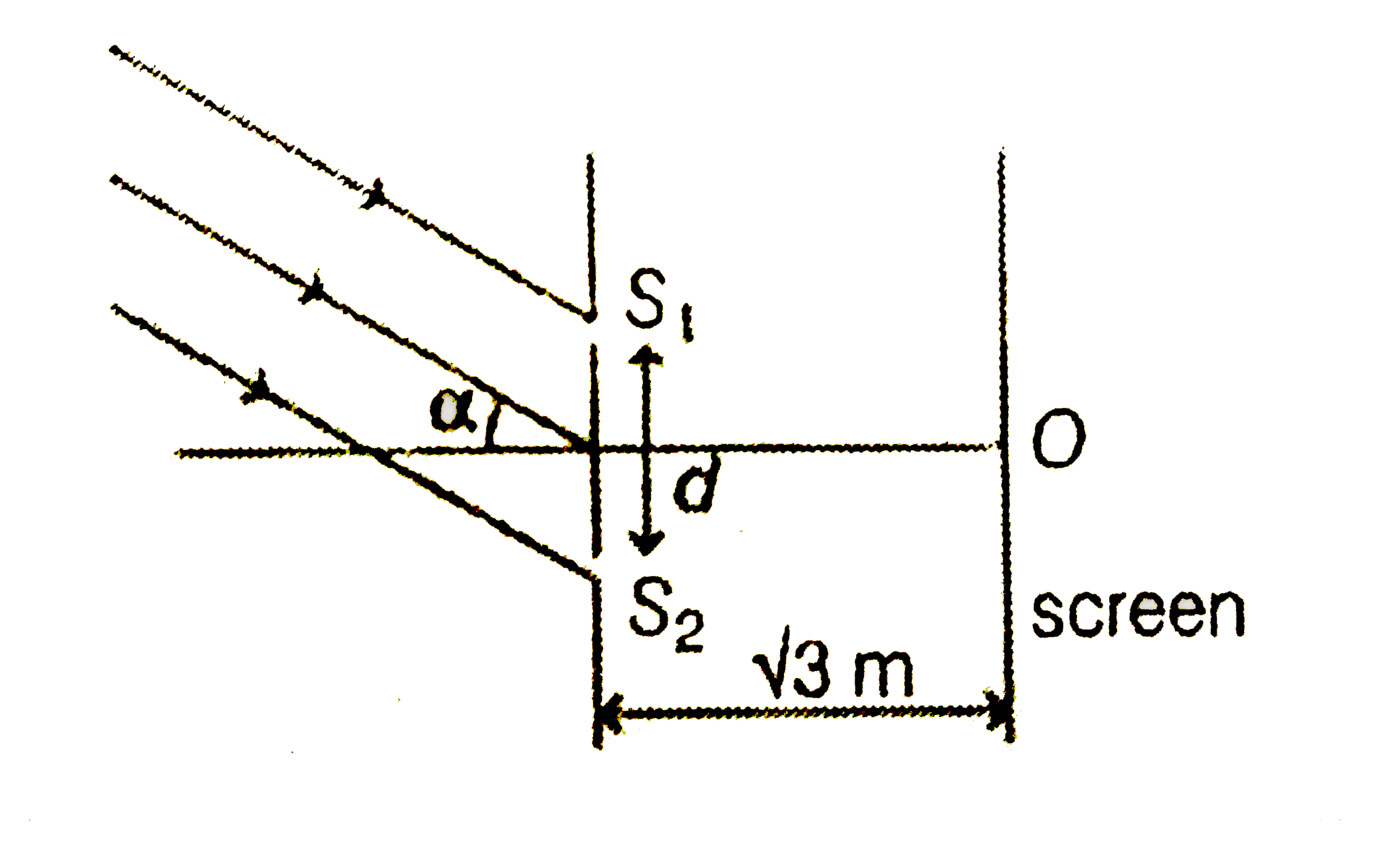
A parrallel beam of light (λ=5000Å) is incident at an angle α=30∘ as shown in YDSE experiment. Intensity due to each slit at any point on screen in I0. The distance between slits is 1mm. The intensity at central point O on the screen is KI0. Find the value of K.
 View Solution
View SolutionIn Young.s double slit experiment, show graphically how intensity of light varies with distance.
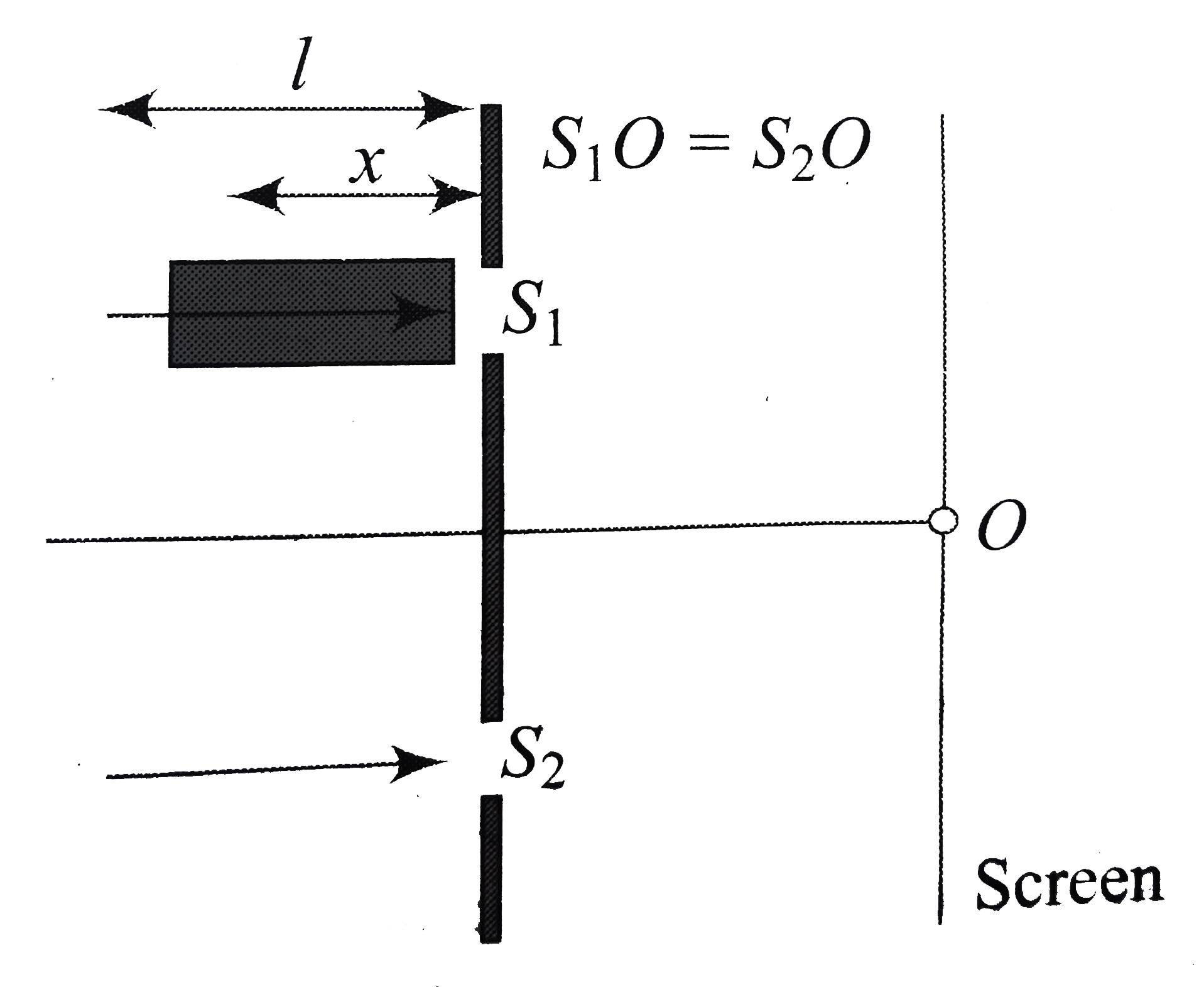
View SolutionIn figure, parallel beam of light is incident on the plane of the slits of a Young's double-slit experiment. Light incident on the slit S1 passes through a medium of variable refractive index μ=1+ax (where 'x' is the distance from the plane of slits as shown), up to distance 'I' before falling on S1. Rest of the space is filled with air. If at 'O' a minima is formed. then the minimum value of the positive constant a (in terms of l and wavelength λ in air) is
 View Solution
View SolutionIn Young.s double slit experiment intensity at a point is (1/4) of the maximum intensity. Angular position of this points is
View SolutionIn the standard Young's double slit experiment, the intensity on the screen at a point distant 1.25 fringe widths from the central maximum is (assuming slits to be identical)
View SolutionIn a Young’s double slit experiment, the source illuminating the slits is changed from blue to violet. The width of the fringes
View SolutionIn Young's double slit experiement when wavelength used is 6000Å and the screen is 40cm from the slits, the fringes are 0.012cm wide. What is the distance between the slits?
View SolutionIn a Young’s double slit experiment, the separation of the two slits is doubled. To keep the same spacing of fringes, the distance D of the screen from the slits should be made
View SolutionA beam of light consisting of two wavelengths, 650 nm and 520 nm is used to obtain interference fringes in Young's double-slit experiment. What is the least distance (in m) from a central maximum where the bright fringes due to both the wavelengths coincide ? The distance between the slits is 3 mm and the distance between the plane of the slits and the screen is 150 cm.
View SolutionThe maximum intensity in Young's double slit experiment is I0 . What will be the intensity of light in front of one the slits on a screen where path difference is λ4 ?
View Solution

